Topic 1:
Title Description: Boredom cows have a sudden idea that they want to have two colors of grid red and blue in their hands. Each grid cow has its own idea. For example, the following grid.

Checks 1 and 2 are blue, Checks 3 are red, Checks 4 are blue, Checks 5 are red, Checks 6 and 7 are blue, and Checks 8 are red. If he paints Chinese in this way, he needs 6 steps (1, 2 can be painted together, 6 and 7 can be painted together). But he can also paint 1-7 blue and 3, 5 and 8 are red, respectively, with a minimum number of steps of 4.
Description: The first question 10 minutes AC, very simple;
Solving ideas:
Three options:
1. Painting with one color and one color;
2. Paint all in red and then in blue;
3. Paint them all in blue and then in red.
Statistics have several colors;
The code is as follows:
#include<iostream>
using namespace std;
int solution(int N, string s) {
//Divide the grid into different blocks by color
if (N == 0) return 0;
char cur = s[0];
int count = 1;
int B_count = (cur == 'B') ? 1 : 0;
for (int i = 1; i < N; ++i) {
if (s[i] != cur) {
if (s[i] == 'B') B_count++;
count++;
cur = s[i];
}
}
return min(count, min(1 + B_count, 1 + count - B_count));
}
int main() {
int N;
cin >> N;
string s;
cin >> s;
cout << solution(N, s) << endl;
}
Question 2:
Title Description: Give two numbers a, b, a each time you multiply a positive integer greater than 1 to get a new a. We call this operation a time it multiplies. Now you can calculate whether a can be multiplied to B by several times.
If a can be multiplied to B several times, calculate the maximum number of times it can be multiplied. If a cannot be changed to b, output-1.
Description: Question 2 AC
Solve the problem by turning the problem into finding the product of the maximum number of factors that can be split into, violent search
The code is as follows:
#include<iostream>
using namespace std;
int maxOperate(int a, int b) {
if (b % a) return -1;
int c = b / a;
int nums = 0;
while (c != 1) {
int limit = c;
for (int i = 2; i <= limit; ++i) {
if (c == 1) break;
if (!(c % i)) {
c /= i;
++nums;
break;
}
}
}
return nums;
}
int main() {
int a, b;
cin >> a >> b;
cout << maxOperate(a, b) << endl;
}Question 3:
Title Description: For a string containing only English letters, you can change the characters in it at different costs depending on the type of change:
* It costs 5 to change one letter to another with the same case
* Changing a letter from uppercase to lowercase or from lowercase to uppercase costs 5
Now, what is the minimum cost of assigning a string containing only English letters to contain the substring AcMer?
Description: Question 3 AC
Solving ideas:
1. For strings of length 5, there are several cases where the cost of each character is calculated directly:
1. They are all uppercase or lowercase and cost 5
2, the same letter in upper and lower case, costs 5
3. In other cases, the cost is 10
2. For strings longer than 5, slide the window directly, with a window size of 5, recording the minimum cost
The code is as follows:
#include<iostream>
#include<algorithm>
using namespace std;
int minCostHelper(string& s, string& p, int start) {
//This function only calculates the cost between a substring of length 5 and a pattern
// AcMer
// 1. Determine if two letters are equal
// 2. Determine if two letters are case-sensitive
// 3. Determine if both letters are capitalized or lowercase
// AcAer AcMer
int cost = 0;
for (int i = 0; i < 5; ++i) {
if (s[start + i] == p[i]) {
continue;
}
else if (abs(s[start + i] - p[i]) == 32) {
cost += 5;
}
else if (s[start + i] >= 'a' && s[start + i] <= 'z' && p[i] >= 'a' && p[i] <= 'z') {
cost += 5;
}
else if (s[start + i] >= 'A' && s[start + i] <= 'Z' && p[i] >= 'A' && p[i] <= 'Z') {
cost += 5;
}
else {
cost += 10;
}
}
return cost;
}
int minCost(string& s, string& p) {
if (s == p) return 0;
if (s.size() == 5) {
return minCostHelper(s, p, 0);
}
int min_cost = INT_MAX;
for (int i = 0; i <= s.size() - 5; ++i) {
min_cost = min(min_cost, minCostHelper(s, p, i));
}
return min_cost;
}
int main() {
string s;
cin >> s;
string p = "AcMer";
cout << minCost(s, p) << endl;
}
Question 4:
Title Description: Niu Niu has a positive integer n. Niu Niu wants you to divide n into an equal ratio column with the first item 1 and the sum of the equal ratio columns is n. Niu Niu wants more items of the equal ratio columns as good as possible. Please output the number of items of the equal ratio columns and the metric ratio (metric >=2).
Note: The pass rate of this topic is 0. Both the examples and some examples written by me have passed. I don't know where the problem is.
Solving ideas:
Equal ratio column formula:
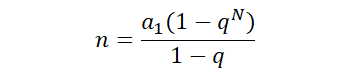
The first n items and the input n, N are the number of items. We want to find the most items, that is, the smaller the public ratio, the better. So we start with the public ratio=2.
By calculating the sum of the first N terms, we know that the sum of the first N terms must be an integer, so the answer is to find the first N term and the one that is an integer.
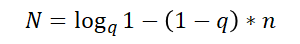
The code is as follows:
#include<iostream>
#include<math.h>
#include<vector>
using namespace std;
vector<int> solution(int n) {
// Golby q
// Number of Items N
long
long int X, N, N_int;
int q_res;
double N_d, error;
for (int q = 2; q < n; ++q) {
X = 1 - n * (1 - q);
N_d = log(X) / log(q);
N_int = int(log(X) / log(q));
error = N_d - N_int;
if (error == (double)0.0) {
N = (int)(log(X) / log(q));
q_res = q;
break;
}
}
return { N, q_res };
}
int main() {
int t;
cin >> t;
int n;
vector<int> res;
for (int i = 0; i < t; ++i) {
cin >> n;
res = solution(n);
for (int i = 0; i < res.size(); ++i) {
if (i == 0) cout << res[i];
else cout << " " << res[i];
}
cout << endl;
}
}