First Good-bye ~I haven't written a summary of the exam for a long time [because I can't change QAQ in the previous few sessions].

1 permut

1.1 Topic

Find out how many inverse pairs of numbers k are in all permutations consisting of N numbers from 1 to n.

1.2 Input

The first action is an integer T, which is the number of data arrays.

The following T lines, each with two integers n, k, have the meaning described in the title.

1.3 Output

Output answers for each set of data and the results after taking the model for 10000

1.4 Sample Input

1

4 1

1.5 Sample Output

3

1.6 Data

For 30% of the data, n < 12 is satisfied.

For all data, it satisfies n < 1000, k < 1000, T < 10.

1.7 Problem Solution

This question has the same meaning as Luogu's inversion order. The so-called reverse order pair means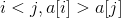Such a pair of i, j. So if the order is 3,2,1, then there are three reverse pairs.

The number of solutions to this problem. Seeing this, we can generally think of two solutions: number theory combination number and dp. It's obvious that DP is much more convenient.

How about dp? Ben Li wrote out all the permutations of 4 by hand and worked out the number of their respective reverse order pairs. Combining with the recurrence of dp, we can think that if there is a 3 arrangement now, you need to insert 4 into it and put it in the last place with the reverse logarithm unchanged; put forward a position, +1; put forward a position, +2... By analogy, you can add 3, or 4-1, to the front. So we can set it up.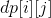Represents the number of cases where the first i number and the inverse logarithm are j pairs.

Enumeration of each insertion method is available:.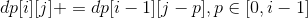

This is the core code of this topic. Last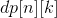That is what we want.

Upper Code——

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#define maxn 1005
const int mod = 10000;
using namespace std;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int n, k, T;
int dp[maxn][maxn];
signed main() {
	T = read();
	while(T--) {
		n = read(), k = read();
		memset(dp, 0, sizeof dp);//This question has many sets of data, so we need memset.
		
		for(int i = 1; i <= n; i++) {
			dp[i][0] = 1;//Initialization
			for(int j = 1; j <= k; j++) {
				for(int p = i - 1 ; p >= 0; p--)//It's both positive and negative here, and that's what you need to do if you want to scroll.
					if(j >= p) dp[i][j] = (dp[i][j] + dp[i - 1][j - p]) % mod;
//				printf("dp[%d][%d] = %d\n", i, j, dp[i][j]);
			}
		}
		
		printf("%d\n", dp[n][k]);
	}
}

The first question is still water. [However, I lost 70 points because I didn't decide if J >= P... ]

2 beautiful

2.1 Topic

For a sequence of length n, there is a graceful value for the number ai of each position i, which is defined as: finding the most in the sequence

A long section of [l, r], satisfying l < i < r, and the median of [l, r] is ai (when we compare the number of two positions in the sequence,

Number is the first keyword and subscript is the second keyword. In this way, the length of [l, r] may only be odd, and r - l + 1 is the fine value of i.

Next, there are Q queries, and each query [l, r] represents the maximum graceful value in the query interval [l, r].

2.2 Input

The first line enters n followed by n integers, representing ai followed by Q, representing Q intervals followed by Q lines, each line

Two integers l, r(l < r), representing the left and right endpoints of the interval

2.3 Output

For each interval, output the answer

2.4 Sample Input

8
16 19 7 8 9 11 20 16
8
3 8
1 4
2 3
1 1
5 5
1 2
2 8
7 8

2.5 Sample Output

7
3
1
3
5
3
7
3

2.6 Data

For 30% of the data, satisfy n, Q < 50

For 70% of the data, satisfy n, Q < 2000

For all data, it satisfies n < 2000, Q < 100000,ai < 200.

2.7 Problem Solution

Super happy!! This question has come up with its own way of doing it!!!

But the title description is disgusting. It took a long time to understand.

That is to say, give you a sequence of length n, the number i is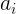At the same time, there is a concept called graceful value, that is, to be able to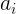The length of the largest interval in the median is the fine value of i. Give you Q questions. Each question contains an interval. Ask you what is the maximum graceful value in the interval.

Obviously, when it comes to inquiry, it's just a normal RMQ. Just maintain the segment tree. [There are many ways, of course.) The key is how to deal with the graceful value of each point. As we know, as a median, it means that the interval is greater than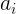Number and less than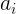The number is the same. So we can think of: diverge from i to left and right sides, define a cnt, encounter greater than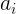If it's less than - 1, then the two sides match each other.

Specific operation is: diverge to one side, use map record value as the subscript position of cnt and so on; then diverge to the other side, and count cnt again to see if there is a match for 0 on the previous side. That's probably the case.Preprocessing [map constants are temporarily ignored...

So the train of thought is divided into two parts... Of course, it is also useful for the second part of the differential solution, let's not talk about it here.~

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#include<map>
#define maxn 2005
using namespace std;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int n, a[maxn], cnt, be[maxn];
int mx[maxn << 2];
map<int, int> mp;
void build(int p, int l, int r) {//Build up trees
	if(l == r) {mx[p] = be[l]; return;}
	int mid = l + r >> 1;
	build(p << 1, l, mid), build(p << 1 | 1, mid + 1, r);
	mx[p] = max(mx[p << 1], mx[p << 1 | 1]);
}

int ask(int p, int l, int r, int ls, int rs) {//query
	if(ls <= l && r <= rs) return mx[p];
	int mid = l + r >> 1, ans = 0;
	if(ls <= mid) ans = max(ans, ask(p << 1, l, mid, ls, rs));
	if(rs > mid) ans = max(ans, ask(p << 1 | 1, mid + 1, r, ls, rs));
	return ans;
}

signed main() {
	n = read();
	for(int i = 1; i <= n; i++) a[i] = read();
	
	for(int i = 1; i <= n; i++) {
		be[i] = 1;
		mp.clear(); cnt = 0;
		for(int j = i - 1; j; j--) {
			if(a[j] <= a[i]) cnt--;//Go to the left
			else cnt++; mp[cnt] = i - j;
			if(!cnt) be[i] = max(be[i], i - j + 1);//In fact, I'm dealing with a lot of trouble here...
		}
		
		cnt = 0;
		for(int j = i + 1; j <= n; j++) {
			if(a[j] >= a[i]) cnt++;
			else cnt--; 
			if(!cnt || mp[0 - cnt]) be[i] = max(be[i], j - i + mp[0 - cnt] + 1);
            //Here's a better way to deal with it.
		}
	}
	
	build(1, 1, n);//Segment tree
	int Q = read(), l, r;
	while(Q--) {
		l = read(), r = read();
		printf("%d\n", ask(1, 1, n, l, r));
	}
	return 0;
}
/*
9
3 7 9 10 1 2 0 3 4
9
1 1
2 2
3 3
4 4 
5 5
6 6
7 7
8 8
9 9
*/

3 subset

3.1 Topic

At first you have an empty set, which can have duplicate elements, and then Q operations.

1. add s

Add the number s to the collection.

2. del s

Delete the number s in the collection. Guarantee the existence of S

3. cnt s

Number of queries that satisfy a&s = a condition

3.2 Input

The first line is an integer Q, and the next line is Q. Each line is one of three operations.

3.3 Output

Output answers for each cnt operation

3.4 Sample Input

7
add 11
cnt 15
add 4
add 0
cnt 6
del 4
cnt 15

3.5 Sample Output

1
2
2

3.6 Data

For 30% of the data, it satisfies: 1 < n < 1000

For 100% data, 1 < n < 200000, 0 < s < 2 ^ 16

3.7 Question Solution

It's easy to get 30 minutes of violence on this topic. Let's not talk about it. Arrays, vector s are fine.

The correct explanation is a block thought. [First of all, let the official questions be answered directly:

In fact, however, it is not very easy to understand how to actually operate.

For add and delete, it is equivalent to fixing the prefix of read x, that is, the first eight bits, and looking at the last eight bits. Because the cnt statement asks for the number of numbers whose original values remain unchanged after the value given above, we have to reverse the adds and deletes to use the existing number x to correspond to the enumerated value i. If &after X or x, then the contribution to the worthwhile answer of u is 1.

All in all, it's... Two kinds of operations, one enumeration prefix, fixed suffix, one fixed suffix, enumeration prefix, as long as the two operations are opposite. I'm writing the opposite kind of questions...

This question is a bit unclear. But that's the way of thinking.

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
using namespace std;
const int maxn = 1 << 8;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int x, n, sum[maxn][maxn];
char op[maxn];
void add(int x) {
	int a = x >> 8, b = x - (a << 8);//a is the top 8 and b is the bottom 8.
	for(int i = 0; i < maxn; i++) if((i & a) == a) sum[i][b]++;//Use a to correspond to the contributed i
}

void cut(int x) {
	int a = x >> 8, b = x - (a << 8);
	for(int i = 0; i < maxn; i++) if((i & a) == a) sum[i][b]--;//Empathy
}

int find(int x) {
	int ans = 0, a = x >> 8, b = x - (a << 8);
	for(int i = 0; i < maxn; i++) if((i & b) == i) ans += sum[a][i];//i is the main body.
	return ans;
}

signed main() {
	n = read();
	for(int i = 1; i <= n; i++) {
		scanf("%s %d", op, &x);
		if(op[0] == 'a') add(x);
		else if(op[0] == 'd') cut(x);
		else printf("%d\n", find(x));
	}
	return 0;
}

QwQ Welcome Comments

-End-