meaning of the title

Given a permutation a [n, 1.2n-1], defined a[i,j]=a[i-1,j-1],a[i-1,j],a[i-1,j+1] i n three numbers, and asked what the value of a[1,n] was.
n<=100000

Analysis

Firstly, we can divide the answer into two parts. Then we can regard the number less than mid as 0 and the rest as 1. Then the median becomes the mode.
Look at the nature:
Note that if the bottom row has two adjacent zeros, then both columns will be zero.
Then if 0 and 1 are crossed, their lengths become smaller and smaller, and the last two 01 intervals intersect, as shown in the following figure: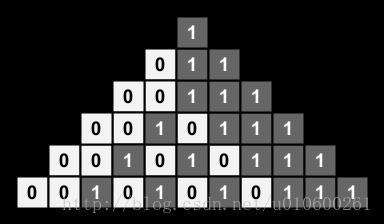

Then we can figure out the coverage of the last paragraph, and we can know the answer.

Code

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=200005;

int n,m,a[N],b[N];
struct data{int l,r,c;}in[N];

int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

bool check(int lim)
{
    for (int i=1;i<=m;i++) b[i]=(a[i]>=lim);
    int tot=0;
    for (int l=1;l<=m;l++)
    {
        int r=l;
        while (r<m&&b[r+1]==b[l]) r++;
        if (l==r) continue;
        in[++tot]=(data){l,r,b[l]};
        l=r;
    }
    if (!tot) return b[1];
    in[0].r=0;
    for (int i=1;i<=tot;i++)
    {
        int l=in[i-1].r+1,r=in[i].l-1;
        if (l>r) continue;
        int mid=(l+r)/2;
        in[i-1].r=mid;in[i].l=mid+1;
    }
    int l=in[tot].r+1,r=m,mid=(l+r)/2;
    if (l<=r) in[tot].r=mid;
    for (int i=1;i<=tot;i++) if (in[i].l<=n&&in[i].r>=n) return in[i].c;
}

int main()
{
    n=read();m=n*2-1;
    for (int i=1;i<=m;i++) a[i]=read();
    int l=1,r=m;
    while (l<=r)
    {
        int mid=(l+r)/2;
        if (check(mid)) l=mid+1;
        else r=mid-1;
    }
    printf("%d",l-1);
    return 0;
}