Title Description

The generals of the command are going to be in n × M's grid map deploys their artillery forces. An n × The map of M consists of N rows and m columns. Each grid of the map may be mountainous (represented by H) or plain (represented by P), as shown in the following figure. At most one artillery unit can be deployed on each grid of plain terrain (artillery units cannot be deployed on mountains); The attack range of an Artillery Force on the map is shown in the black area in the figure:

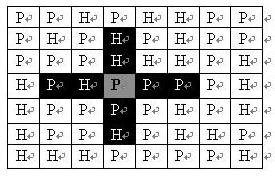
If an artillery unit is deployed on the upper part of the plain marked by gray in the map, the black grid in the map indicates the area it can attack: two grids on the left and right in the transverse direction and two grids on the top and bottom in the longitudinal direction. Other white grids in the figure cannot be attacked. It can be seen from the picture that the artillery's attack range is not affected by the terrain.

Now, the generals plan how to deploy artillery units. On the premise of preventing accidental injury (ensuring that no two artillery units can attack each other, that is, no artillery unit is within the attack range of other artillery units), how many artillery units of our army can be placed in the whole map area at most.

input

The first line contains two positive integers separated by spaces, representing N and M respectively;
The next N lines contain M consecutive characters (P or H) with no spaces in the middle. The data of each row in the map is represented in order.

output

Only one line, including an integer K, represents the maximum number of artillery units that can be placed.

sample input

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

sample output

6

Tips

[data range and prompt]

N≤100,M≤10.

Problem solution

        Let's talk about initialization first. Obviously, the m range of this problem suggests that we need binary compression. Therefore, the first step is to compress all possible artillery deployment states in 1 row with binary. 1 means artillery and 0 means no artillery. Then, the number of Artillery (1) in each state is processed with lowbit and stored with sum array to facilitate the calculation of the total number of artillery. For each line of map, it is also stored in binary. If you can't put artillery, it is 1, and if you can put artillery, it is 0. In this way, first initialize which possible artillery arrangements can be accepted by each line of map. First, the distance between artillery should be greater than 2. Assuming that the artillery status is j at this time, it must be (J & (J < < 1)) 0 and (J & (J < < 2)) 0, which means that each artillery attack will not hurt the artillery in the same row. At the same time, artillery cannot be put on 1 (Highland) on the map. Assuming that the map is i, that is, (i & J) should be 0, it means that there are no artillery on the highland. The above initialization can be understood by drawing by yourself.

        After initialization, now let's see how to do this problem. For a line (the number of lines is greater than 2), whether the current artillery arrangement that meets its own requirements and map requirements can be established depends on whether the artillery arrangement of the previous two lines will conflict with the line, that is, there will not be two artillery in the same position in different lines (otherwise it will attack). This is also very simple. Directly press the position and to see whether it is 0. If it is 0, it means there is no conflict. Of course, There must be no conflict between the two lines. The current total number of artillery is all the current quantity from the previous state plus the quantity of current state 1 (i.e. sum). It is recorded from this line and the previous line and determined together with the up line.

        Therefore, dp[i][j][k] is used to represent the maximum total number of artillery in the k-th behavior j and the k-1 behavior I. As for why two lines should be recorded, because the artillery's attack range is cross, and the least that can transfer the state is two-dimensional (three-dimensional can also be used. First, the memory can't be opened, but it's unnecessary. It can be transferred with max), but the memory is limited. Therefore, consider converting K into 3, that is, rolling array.

        The first and second lines need to be processed separately. The previous line of the first line is 0 (it can be regarded as nonexistent and will not affect the answer). The maximum value of the artillery is the maximum value of the current line. The previous line of the second line is the first line, and the second line is the second line. The maximum value of the artillery at the moment is the maximum value of the current 2 lines. Then the scrolling array can be solved by (i%3), or it can be written by your own ideas.

        The final answer? It must be the maximum in all cases where line (n-1) is transferred to line n. Therefore, enumerating the total state of the last two lines can quickly get the answer. I used the pt array to quickly memorize the artillery order that each map can meet the conditions, which can save a lot of time.

Reference code

#include<cstdio>
using namespace std;
int n,m;char s[200];
int e_map[200],sum[1025];
int pt[1025][1025],ans=0;
int dp[1025][1025][3];
int max1(int p,int q) { return p>q?p:q; }
int getsum(int k)
{
	int ret=0;
	while(k) { ret++;k-=k&-k; }
	return ret;
}
int main() 
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s);
		for(int j=0;j<n;j++)
		if(s[j]=='H') e_map[i]|=(1<<j);
		for(int j=0;j<(1<<m);j++)
		if((j&e_map[i])==0&&(j&(j<<1))==0&&(j&(j<<2))==0)
		pt[i][++pt[i][0]]=j;
	}
	for(int i=0;i<(1<<m);i++) sum[i]=getsum(i);
	for(int i=1;i<=pt[1][0];i++)
	dp[0][pt[1][i]][1]=sum[pt[1][i]];
	for(int i=1;i<=pt[1][0];i++)
		for(int j=1;j<=pt[2][0];j++)
			if(!(pt[1][i]&pt[2][j]))
				dp[pt[1][i]][pt[2][j]][2]=sum[pt[1][i]]+sum[pt[2][j]];
	for(int i=3;i<=n;i++)
		for(int j=1;j<=pt[i-2][0];j++)
			for(int p=1;p<=pt[i-1][0];p++)
				if(!(pt[i-2][j]&pt[i-1][p]))
					for(int q=1;q<=pt[i][0];q++)
						if(!(pt[i][q]&pt[i-1][p])&&!(pt[i][q]&pt[i-2][j]))
						{
							dp[pt[i-1][p]][pt[i][q]][i%3]=max1(
							dp[pt[i-1][p]][pt[i][q]][i%3],
							dp[pt[i-2][j]][pt[i-1][p]][(i+2)%3]+sum[pt[i][q]]);
						}
	for(int i=1;i<=pt[n-1][0];i++)
		for(int j=1;j<=pt[n][0];j++)
			if(!(pt[n-1][i]&pt[n][j]))
				ans=max1(ans,dp[pt[n-1][i]][pt[n][j]][n%3]);
	printf("%d",ans);
	return 0;
}