[artificial intelligence project] Fashion Mnist recognition experiment
This paper mainly carries out the recognition experiment of fashion mnist through four methods, mainly including word bag model, hog feature, mlp multilayer perceptron and cnn convolution neural network. Then don't say much, get up!!!

Fashion Mnist
Fashion MNIST is an image data set containing 70000 gray images covering 10 categories (T-shirts, shoes, etc.). The following image shows the effect of a single dress at a lower resolution (28x28 pixels):

What will be done next?
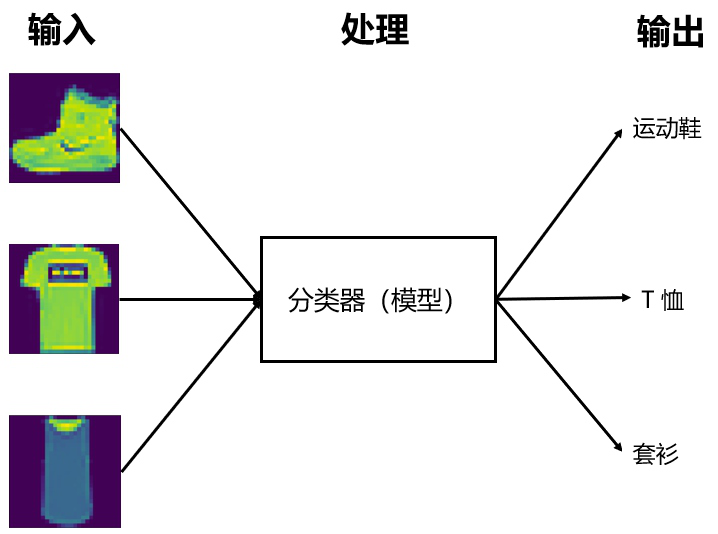
1, Import Fashion Mnist
1. Import module
# Import library import tensorflow as tf from tensorflow import keras import numpy as np import matplotlib.pyplot as plt
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:516: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_qint8 = np.dtype([("qint8", np.int8, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:517: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_quint8 = np.dtype([("quint8", np.uint8, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:518: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_qint16 = np.dtype([("qint16", np.int16, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:519: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_quint16 = np.dtype([("quint16", np.uint16, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:520: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_qint32 = np.dtype([("qint32", np.int32, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:525: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
np_resource = np.dtype([("resource", np.ubyte, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorboard\compat\tensorflow_stub\dtypes.py:541: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_qint8 = np.dtype([("qint8", np.int8, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorboard\compat\tensorflow_stub\dtypes.py:542: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_quint8 = np.dtype([("quint8", np.uint8, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorboard\compat\tensorflow_stub\dtypes.py:543: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_qint16 = np.dtype([("qint16", np.int16, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorboard\compat\tensorflow_stub\dtypes.py:544: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_quint16 = np.dtype([("quint16", np.uint16, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorboard\compat\tensorflow_stub\dtypes.py:545: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
_np_qint32 = np.dtype([("qint32", np.int32, 1)])
D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorboard\compat\tensorflow_stub\dtypes.py:550: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
np_resource = np.dtype([("resource", np.ubyte, 1)])
The skeleton program for downloading and loading the fashion MNIST dataset has been integrated in tf.keras. You only need to import and load the data. 60000 pictures in the dataset are used to train the network, and 10000 pictures are used to evaluate the accuracy of the learned network classification images
Note: in machine learning, we generally divide the data set into training data set and test data set according to the ratio of 8:2. The training data set is used to train the model, and the test data set is used to test the accuracy of the trained model
2. Load dataset
# Load dataset fashion_mnist = keras.datasets.fashion_mnist (train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
After loading the dataset, four Numpy arrays will be returned
- train_images and train_ The labels array is the training set, that is, the data used for learning the model, with a total of 60000 pieces
- Test set test_images and test_ The labels array is used to test the model. There are 10000 in total
- train_images and test_ All images are 28x28 NumPy arrays, and the value of each point is between 0 and 255. Represents the current picture_ Images and test_labels is a 10 dimensional array of integers, and the value of each dimension is between 0 and 9. The labels representing the current image correspond to the category of the clothing represented by the image:
3. Explore data sets
#We first explore the format of the data set, and then train the model. Let's first look at the shape of the pictures in the dataset print(train_images.shape)
(60000, 28, 28)
#Let's take another look at the shape of the label in the dataset print(train_labels.shape)
(60000,)
# visualization ## Create a new image plt.figure() ## Display image (fill in image) plt.imshow(train_images[0]) ## Add a colorbar (color bar or gradient bar) to the subgraph plt.colorbar() ## Set gridlines plt.grid(False)
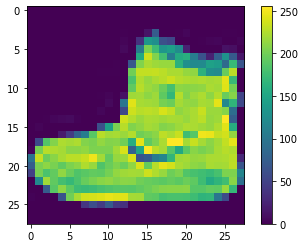
4. View labels
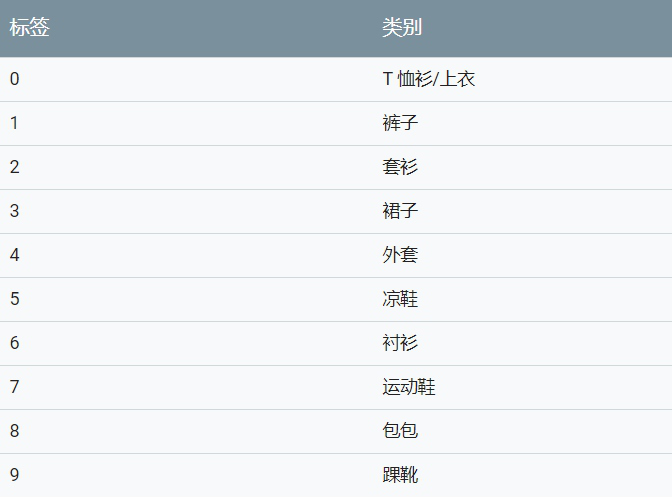
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
print(train_labels[0])
print(class_names[train_labels[0]])
9 Ankle boot
5. Preprocessing normalization operation
We reduce these values in the picture to between 0 and 1, and then feed them to the neural network model. To do this, the data type of the image component is converted from an integer to a floating point number, and then divided by 255. This makes it easier to train. The following is the function of preprocessing images: it is important to preprocess the training set and the test set in the same way:
train_images = train_images / 255.0 test_images = test_images / 255.0
# Display the image after preprocessing plt.figure() plt.imshow(train_images[0]) plt.colorbar() plt.grid(False)
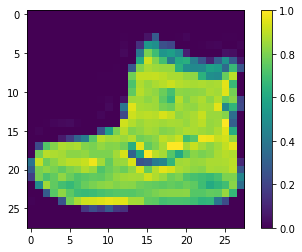
#The first 25 images in the training set are displayed, and the category name is displayed under each image. Verify that the data format is correct, and then we can start building and training the network.
plt.figure(figsize=(10,10))
for i in range(25):
## Generate 5 * 5 subgraphs under the current graph
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
#Displays the category of the current picture
plt.xlabel(class_names[train_labels[i]])

2, Based on word bag model
- (1) The feature points of each image are still extracted, such as SIFT feature points
- (2) For all SIFT feature points of all pictures, kmeans clustering is carried out as a whole, and the words are divided into multiple different classes. The number of classes is defined as wordCount.
- (3) For each picture, calculate the number of SIFT features of different classes, corresponding to one dimension of the feature vector to be obtained. Then we can generate a vector of wordCount dimension for each picture.
Steps to obtain the BoW vector of an image:
- Visual dictionary for constructing image library
- Extract the local features of all images in the image library, such as SIFT
- Cluster the extracted image features, such as k-means, and get that the clustering center is the visual Vocabulary dictionary of the image database
- Calculate the BoW vector of an image
- Extract local features of image
- Count the frequency of each visual word in Vocabulay in the image.
import os import cv2 import pickle import numpy as np import matplotlib.pyplot as plt from imutils import paths from sklearn.cluster import KMeans from scipy.cluster.vq import vq from sklearn.model_selection import train_test_split from sklearn.svm import LinearSVC
print(train_images.shape) print(train_labels.shape) print(test_images.shape) print(test_labels.shape)
(60000, 28, 28) (60000,) (10000, 28, 28) (10000,)
sifts_img = [] # The file names and sift features of all images are stored
limit = 10000 #Maximum number of training
count = 0 # Number of word bag features
num = 0 # Effective number
label = []
for i in range(limit):
img = train_images[i].reshape(28,28)
img = np.uint8(np.double(img) * 255)
sift = cv2.xfeatures2d.SIFT_create()
kp,des = sift.detectAndCompute(img,None)
if des is None:
continue
sifts_img.append(des)
label.append(train_labels[i])
count = count + des.shape[0]
num = num + 1
label = np.array(label)
data = sifts_img[0]
for des in sifts_img[1:]:
data = np.vstack((data, des))
print("train file:",num)
count = int(count / 40)
count = max(4,count)
train file: 9236
# Clustering sift features
k_means = KMeans(n_clusters=int(count), n_init=4)
k_means.fit(data)
# Construct the word bag representation of all samples
image_features = np.zeros([int(num),int(count)],'float32')
for i in range(int(num)):
ws, d = vq(sifts_img[i],k_means.cluster_centers_)# Calculate the visual vocabulary of each sift feature
for w in ws:
image_features[i][w] += 1 # Add 1 to the corresponding visual vocabulary position element
x_tra, x_val, y_tra, y_val = train_test_split(image_features,label,test_size=0.2)
# Construct linear SVM objects and train them
clf = LinearSVC(C=1, loss="hinge").fit(x_tra, y_tra)
# Prediction accuracy of training data
print (clf.score(x_val, y_val))
# save the training model as pickle
with open('bow_kmeans.pickle','wb') as fw:
pickle.dump(k_means,fw)
with open('bow_clf.pickle','wb') as fw:
pickle.dump(clf,fw)
with open('bow_count.pickle','wb') as fw:
pickle.dump(count,fw)
print('Trainning successfully and save the model')
0.6293290043290043 Trainning successfully and save the model D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\sklearn\svm\_base.py:947: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations. "the number of iterations.", ConvergenceWarning)
with open('bow_kmeans.pickle','rb') as fr:
k_means = pickle.load(fr)
with open('bow_clf.pickle','rb') as fr:
clf = pickle.load(fr)
with open('bow_count.pickle','rb') as fr:
count = pickle.load(fr)
target_file = ['T-shirt','Trouser','Pullover',
'Dress','Coat','Sandal','Shirt',
'Sneaker','Bag','Ankle boot']
plt.figure()
cnt = 30
i = 1
while(i<=12):
img = test_images[cnt].reshape(28,28)
cnt = cnt + 1
img = np.uint8(np.double(img) * 255)
sift = cv2.xfeatures2d.SIFT_create()
kp,des = sift.detectAndCompute(img,None)
if des is None:
continue
words, distance = vq(des, k_means.cluster_centers_)
image_features_search = np.zeros((int(count)), "float32")
for w in words:
image_features_search[w] += 1
t = clf.predict(image_features_search.reshape(1,-1))
plt.subplot(3,4,i)
i += 1
plt.imshow(img,'gray')
plt.title(target_file[t[0]])
plt.axis('off')
plt.show()

with open('bow_kmeans.pickle','rb') as fr:
k_means = pickle.load(fr)
with open('bow_clf.pickle','rb') as fr:
clf = pickle.load(fr)
with open('bow_count.pickle','rb') as fr:
count = pickle.load(fr)
i = 0
len = test_images.shape[0]
predict_arr = []
while(i<len):
img = test_images[i].reshape(28,28)
img = np.uint8(np.double(img) * 255)
sift = cv2.xfeatures2d.SIFT_create()
print(i)
kp,des = sift.detectAndCompute(img,None)
if des is None:
i += 1
predict_arr.append(0)
continue
words, distance = vq(des, k_means.cluster_centers_)
image_features_search = np.zeros((int(count)), "float32")
for w in words:
image_features_search[w] += 1
t = clf.predict(image_features_search.reshape(1,-1))
i += 1
predict_arr.append(t[0])
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 9995 9996 9997 9998 9999
from sklearn.metrics import accuracy_score,f1_score,confusion_matrix,classification_report score=accuracy_score(test_labels,predict_arr) print(score)
0.5651
print(classification_report(test_labels,predict_arr))
precision recall f1-score support
0 0.36 0.60 0.45 1000
1 0.72 0.47 0.57 1000
2 0.43 0.47 0.45 1000
3 0.49 0.46 0.47 1000
4 0.45 0.44 0.44 1000
5 0.79 0.74 0.76 1000
6 0.36 0.24 0.29 1000
7 0.74 0.74 0.74 1000
8 0.67 0.66 0.66 1000
9 0.79 0.84 0.81 1000
accuracy 0.57 10000
macro avg 0.58 0.57 0.56 10000
weighted avg 0.58 0.57 0.56 10000
import seaborn as sns from sklearn.metrics import confusion_matrix import matplotlib.pyplot as plt %matplotlib inline sns.set() # Confusion matrix matrix = confusion_matrix(test_labels,predict_arr) print(matrix) sns.heatmap(matrix,annot=True)
[[598 17 56 109 45 20 89 15 38 13] [384 473 11 91 7 2 8 7 15 2] [ 73 22 465 55 192 22 96 15 53 7] [184 46 61 459 63 30 43 33 69 12] [ 47 14 245 45 441 19 119 14 48 8] [ 43 20 9 25 8 740 13 88 16 38] [205 22 161 78 184 23 238 11 59 19] [ 41 6 5 22 7 50 8 743 9 109] [ 71 32 60 49 39 19 44 17 658 11] [ 27 2 3 10 5 17 9 67 24 836]] <matplotlib.axes._subplots.AxesSubplot at 0x1f384714548>

3, Based on HOG feature
Histogram of Oriented Gridients, abbreviated as HOG, is a feature commonly used in the field of computer vision and pattern recognition to describe the local texture of an image. The feature name is also very straightforward, that is, first calculate the gradient values in different directions in an area of the picture, and then accumulate them to obtain a histogram. This histogram can represent this area, that is, as a feature, it can be input into the classifier. Then, let's introduce the specific principle and calculation method of HOG, as well as some extensions.
Because HOG is a local feature, you can't get good results if you directly extract features from a large image. The principle is simple. From the perspective of information theory, for example, a 640 * 480 image has about 300000 pixels, that is, the original data has 300000 dimensional features. If HOG is directly done, even if it is divided into 360 bin s according to 360 degrees, it does not have the ability to represent such a large image. From the perspective of Feature Engineering, generally speaking, only when the image area is relatively small, the histogram based on statistical principle can express the area. If the image area is relatively large, the HOG features of two completely different images may also be very similar. However, if the area is small, this possibility is very small. Finally, the image is divided into many blocks, and then the HOG feature is calculated for each block, which also includes geometric (position) characteristics. For example, for a frontal face, the HOG feature extracted from the image block in the upper left part is generally consistent with the HOG feature of the eye.
import warnings
warnings.filterwarnings("ignore")
import os
import cv2
import pickle
import numpy as np
import matplotlib.pyplot as plt
from imutils import paths
from skimage.feature import hog
from scipy.cluster.vq import vq
from sklearn.svm import LinearSVC
from sklearn.model_selection import train_test_split
limit = train_images.shape[0]
data = [] # HoG characteristics
label = []
for i in range(limit):
img = train_images[i].reshape(28,28)
img = np.uint8(np.double(img) * 255)
fd = hog(img)
data.append(fd)
label.append(train_labels[i])
data = np.array(data)
label = np.array(label)
x_tra, x_val, y_tra, y_val = train_test_split(data,label,test_size=0.2)
print('train file:',y_tra.size)
print('val file:',y_val.size)
# Construct linear SVM objects and train them
clf = LinearSVC(C=1, loss="hinge").fit(x_tra, y_tra)
# Prediction accuracy of training data
print ('accuracy:',clf.score(x_val, y_val))
# save the training model as pickle
with open('hog.pickle','wb') as fw:
pickle.dump(clf,fw)
print('Trainning successfully and save the model')
train file: 48000 val file: 12000 accuracy: 0.799 Trainning successfully and save the model
with open('hog.pickle','rb') as fr:
clf = pickle.load(fr)
target_file = ['T-shirt','Trouser','Pullover',
'Dress','Coat','Sandal','Shirt',
'Sneaker','Bag','Ankle boot']
plt.figure()
cnt = 30
i = 1
while(i<=12):
img = test_images[cnt].reshape(28,28)
cnt = cnt + 1
img = np.uint8(np.double(img) * 255)
fd = hog(img)
t = clf.predict([fd])
plt.subplot(3,4,i)
i += 1
plt.imshow(img,'gray')
plt.title(target_file[t[0]])
plt.axis('off')
plt.show()

with open('hog.pickle','rb') as fr:
clf = pickle.load(fr)
i = 0
len = test_images.shape[0]
predict_arr = []
while(i<len):
img = test_images[i].reshape(28,28)
img = np.uint8(np.double(img) * 255)
fd = hog(img)
t = clf.predict([fd])
i += 1
predict_arr.append(t[0])
from sklearn.metrics import accuracy_score,f1_score,confusion_matrix,classification_report score=accuracy_score(test_labels,predict_arr) print(score)
0.7904
print(classification_report(test_labels,predict_arr))
precision recall f1-score support
0 0.70 0.81 0.75 1000
1 0.94 0.94 0.94 1000
2 0.62 0.71 0.67 1000
3 0.79 0.82 0.81 1000
4 0.61 0.79 0.69 1000
5 0.92 0.89 0.90 1000
6 0.47 0.16 0.24 1000
7 0.87 0.90 0.88 1000
8 0.91 0.94 0.92 1000
9 0.94 0.94 0.94 1000
accuracy 0.79 10000
macro avg 0.78 0.79 0.77 10000
weighted avg 0.78 0.79 0.77 10000
import seaborn as sns from sklearn.metrics import confusion_matrix import matplotlib.pyplot as plt %matplotlib inline sns.set() # Confusion matrix matrix = confusion_matrix(test_labels,predict_arr) print(matrix) sns.heatmap(matrix,annot=True)
[[811 15 50 48 21 3 37 0 14 1] [ 3 943 10 32 4 0 7 0 1 0] [ 37 1 715 15 166 1 51 0 14 0] [ 25 33 31 817 50 0 37 0 6 1] [ 16 5 103 50 790 0 27 0 9 0] [ 0 0 0 2 1 890 3 86 5 13] [253 8 228 57 253 0 159 0 42 0] [ 0 0 0 0 0 59 1 897 1 42] [ 6 2 8 8 9 8 13 2 943 1] [ 0 0 0 0 0 10 2 45 4 939]] <matplotlib.axes._subplots.AxesSubplot at 0x1f382c92408>

4, MLP multilayer perceptron
MLP (Multilayer Perceptron) is also called Artificial Neural Network (ANN). In addition to the input and output layer, it can have multiple hidden layers. The simplest MLP contains only one hidden layer, that is, a three-layer structure
import numpy as np from keras.models import Sequential from keras.layers import Dense, Dropout, Flatten, Activation from keras.layers import Conv2D, MaxPooling2D from keras.utils.vis_utils import plot_model from keras.utils import np_utils
X_train = train_images.reshape((-1,784)) X_test = test_images.reshape(-1,784) Y_train = np_utils.to_categorical(train_labels,num_classes=10) Y_test = np_utils.to_categorical(test_labels,num_classes=10)
# Build MLP
model = Sequential()
model.add(Dense(units=256,
input_dim=784,
kernel_initializer='normal',
activation='relu'))
model.add(Dense(units=10,
kernel_initializer='normal',
activation='softmax'))
model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 256) 200960 _________________________________________________________________ dense_4 (Dense) (None, 10) 2570 ================================================================= Total params: 203,530 Trainable params: 203,530 Non-trainable params: 0 _________________________________________________________________
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, Y_train, batch_size=500, epochs=10, verbose=1, validation_data=(X_test, Y_test))
model.save('mlp_fashion_mnist.h5')
WARNING:tensorflow:From D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\tensorflow\python\ops\math_grad.py:1250: add_dispatch_support.<locals>.wrapper (from tensorflow.python.ops.array_ops) is deprecated and will be removed in a future version. Instructions for updating: Use tf.where in 2.0, which has the same broadcast rule as np.where WARNING:tensorflow:From D:\software\Anaconda\anaconda\envs\tensorflow\lib\site-packages\keras\backend\tensorflow_backend.py:977: The name tf.assign_add is deprecated. Please use tf.compat.v1.assign_add instead. Train on 60000 samples, validate on 10000 samples Epoch 1/10 60000/60000 [==============================] - 28s 459us/step - loss: 0.6751 - acc: 0.7771 - val_loss: 0.4986 - val_acc: 0.8310 Epoch 2/10 60000/60000 [==============================] - 1s 19us/step - loss: 0.4437 - acc: 0.8480 - val_loss: 0.4469 - val_acc: 0.8400 Epoch 3/10 60000/60000 [==============================] - 2s 31us/step - loss: 0.3997 - acc: 0.8609 - val_loss: 0.4300 - val_acc: 0.8481 Epoch 4/10 60000/60000 [==============================] - 1s 18us/step - loss: 0.3749 - acc: 0.8682 - val_loss: 0.4151 - val_acc: 0.8546 Epoch 5/10 60000/60000 [==============================] - 1s 18us/step - loss: 0.3512 - acc: 0.8767 - val_loss: 0.3819 - val_acc: 0.8646 Epoch 6/10 60000/60000 [==============================] - 1s 19us/step - loss: 0.3345 - acc: 0.8819 - val_loss: 0.3882 - val_acc: 0.8625 Epoch 7/10 60000/60000 [==============================] - 1s 19us/step - loss: 0.3224 - acc: 0.8855 - val_loss: 0.3654 - val_acc: 0.8725 Epoch 8/10 60000/60000 [==============================] - 1s 19us/step - loss: 0.3086 - acc: 0.8889 - val_loss: 0.3558 - val_acc: 0.8723 Epoch 9/10 60000/60000 [==============================] - 1s 18us/step - loss: 0.2980 - acc: 0.8926 - val_loss: 0.3548 - val_acc: 0.8744 Epoch 10/10 60000/60000 [==============================] - 1s 19us/step - loss: 0.2879 - acc: 0.8963 - val_loss: 0.3560 - val_acc: 0.8719
from keras.models import load_model
model = load_model('mlp_fashion_mnist.h5')
plt.figure()
cnt = 30
i = 1
while(i<=12):
img = [X_test[cnt]]
cnt = cnt + 1
img = np.uint8(np.double(img) * 255)
t = model.predict(img)
result = np.argmax(t, axis=1)
plt.subplot(3,4,i)
i += 1
plt.imshow(img[0].reshape(28,28),'gray')
plt.title(target_file[result[0]])
plt.axis('off')
plt.show()

loss, accuracy = model.evaluate(X_test, Y_test, verbose=0)
print('loss:', loss)
print('accuracy:', accuracy)
loss: 0.35601275362968443 accuracy: 0.8719
predict = model.predict_classes(X_test) from sklearn.metrics import accuracy_score,f1_score,confusion_matrix,classification_report score=accuracy_score(test_labels,predict) print(score)
0.8719
print(classification_report(test_labels,predict))
precision recall f1-score support
0 0.81 0.86 0.83 1000
1 0.97 0.97 0.97 1000
2 0.79 0.74 0.76 1000
3 0.85 0.90 0.87 1000
4 0.72 0.87 0.79 1000
5 0.97 0.94 0.96 1000
6 0.78 0.55 0.65 1000
7 0.93 0.95 0.94 1000
8 0.96 0.97 0.96 1000
9 0.95 0.96 0.96 1000
accuracy 0.87 10000
macro avg 0.87 0.87 0.87 10000
weighted avg 0.87 0.87 0.87 10000
import seaborn as sns from sklearn.metrics import confusion_matrix import matplotlib.pyplot as plt %matplotlib inline sns.set() # Confusion matrix matrix = confusion_matrix(test_labels,predict) print(matrix) sns.heatmap(matrix,annot=True)
[[858 2 14 44 5 2 62 0 13 0] [ 2 971 0 21 4 0 1 0 1 0] [ 22 3 739 15 173 0 46 0 2 0] [ 15 22 12 895 36 0 16 0 4 0] [ 0 1 62 30 874 0 29 0 4 0] [ 0 0 0 1 0 945 0 35 2 17] [161 4 100 45 123 0 551 0 16 0] [ 0 0 0 0 0 16 0 955 0 29] [ 4 1 7 4 6 3 0 5 970 0] [ 0 0 0 0 0 7 1 31 0 961]] <matplotlib.axes._subplots.AxesSubplot at 0x1f383b67a48>

5, CNN convolutional neural network
import numpy as np from keras.models import Sequential from keras.layers import Dense, Dropout, Flatten, Activation from keras.layers import Conv2D, MaxPooling2D from keras.utils.vis_utils import plot_model from keras.utils import np_utils
X_train = train_images.reshape((-1,28,28,1)) X_test = test_images.reshape(-1,28,28,1) Y_train = np_utils.to_categorical(train_labels,num_classes=10) Y_test = np_utils.to_categorical(test_labels,num_classes=10)
# Build LeNet-5 model = Sequential() model.add(Conv2D(filters=6, kernel_size=(5, 5), padding='valid', input_shape=(28, 28, 1), activation='relu')) # C1 model.add(MaxPooling2D(pool_size=(2, 2))) # S2 model.add(Conv2D(filters=16, kernel_size=(5, 5), padding='valid', activation='relu')) # C3 model.add(MaxPooling2D(pool_size=(2, 2))) # S4 model.add(Flatten()) model.add(Dense(120, activation='tanh')) # C5 model.add(Dense(84, activation='tanh')) # F6 model.add(Dense(10, activation='softmax')) # output model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_3 (Conv2D) (None, 24, 24, 6) 156 _________________________________________________________________ max_pooling2d_3 (MaxPooling2 (None, 12, 12, 6) 0 _________________________________________________________________ conv2d_4 (Conv2D) (None, 8, 8, 16) 2416 _________________________________________________________________ max_pooling2d_4 (MaxPooling2 (None, 4, 4, 16) 0 _________________________________________________________________ flatten_2 (Flatten) (None, 256) 0 _________________________________________________________________ dense_8 (Dense) (None, 120) 30840 _________________________________________________________________ dense_9 (Dense) (None, 84) 10164 _________________________________________________________________ dense_10 (Dense) (None, 10) 850 ================================================================= Total params: 44,426 Trainable params: 44,426 Non-trainable params: 0 _________________________________________________________________
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, Y_train, batch_size=500, epochs=10, verbose=1, validation_data=(X_test, Y_test))
model.save('cnn_fashion_mnist.h5')
Train on 60000 samples, validate on 10000 samples Epoch 1/10 60000/60000 [==============================] - 3s 44us/step - loss: 0.3044 - acc: 0.8892 - val_loss: 0.3304 - val_acc: 0.8774 Epoch 2/10 60000/60000 [==============================] - 2s 34us/step - loss: 0.2902 - acc: 0.8948 - val_loss: 0.3259 - val_acc: 0.8809 Epoch 3/10 60000/60000 [==============================] - 2s 35us/step - loss: 0.2826 - acc: 0.8967 - val_loss: 0.3145 - val_acc: 0.8865 Epoch 4/10 60000/60000 [==============================] - 2s 33us/step - loss: 0.2724 - acc: 0.9002 - val_loss: 0.3158 - val_acc: 0.8862 Epoch 5/10 60000/60000 [==============================] - 2s 33us/step - loss: 0.2683 - acc: 0.9025 - val_loss: 0.3174 - val_acc: 0.8843 Epoch 6/10 60000/60000 [==============================] - 2s 34us/step - loss: 0.2610 - acc: 0.9047 - val_loss: 0.3040 - val_acc: 0.8900 Epoch 7/10 60000/60000 [==============================] - 2s 34us/step - loss: 0.2519 - acc: 0.9082 - val_loss: 0.3015 - val_acc: 0.8904 Epoch 8/10 60000/60000 [==============================] - 2s 33us/step - loss: 0.2481 - acc: 0.9086 - val_loss: 0.3097 - val_acc: 0.8877 Epoch 9/10 60000/60000 [==============================] - 2s 34us/step - loss: 0.2432 - acc: 0.9107 - val_loss: 0.2940 - val_acc: 0.8936 Epoch 10/10 60000/60000 [==============================] - 2s 34us/step - loss: 0.2355 - acc: 0.9134 - val_loss: 0.2934 - val_acc: 0.8924
loss, accuracy = model.evaluate(X_test, Y_test, verbose=0)
print('loss:', loss)
print('accuracy:', accuracy)
loss: 0.29342212826013564 accuracy: 0.8924
predict = model.predict_classes(X_test) from sklearn.metrics import accuracy_score,f1_score,confusion_matrix,classification_report score=accuracy_score(test_labels,predict) print(score)
0.8924
print(classification_report(test_labels,predict))
precision recall f1-score support
0 0.80 0.88 0.84 1000
1 0.99 0.97 0.98 1000
2 0.81 0.87 0.84 1000
3 0.88 0.91 0.90 1000
4 0.83 0.82 0.83 1000
5 0.97 0.97 0.97 1000
6 0.75 0.62 0.68 1000
7 0.92 0.97 0.95 1000
8 0.97 0.98 0.97 1000
9 0.98 0.94 0.96 1000
accuracy 0.89 10000
macro avg 0.89 0.89 0.89 10000
weighted avg 0.89 0.89 0.89 10000
import seaborn as sns from sklearn.metrics import confusion_matrix import matplotlib.pyplot as plt %matplotlib inline sns.set() # Confusion matrix matrix = confusion_matrix(test_labels,predict) print(matrix) sns.heatmap(matrix,annot=True)
[[876 1 20 26 5 2 59 0 11 0] [ 1 971 0 20 3 0 3 0 2 0] [ 16 1 869 11 53 1 47 0 2 0] [ 21 2 10 911 21 1 30 0 3 1] [ 3 1 83 35 819 0 58 0 1 0] [ 1 0 0 2 0 967 0 22 0 8] [170 1 84 25 82 0 622 0 16 0] [ 0 0 0 0 0 15 0 973 0 12] [ 5 1 3 3 1 2 4 5 976 0] [ 0 0 0 0 0 7 1 52 0 940]] <matplotlib.axes._subplots.AxesSubplot at 0x1f4444938c8>

Summary
So this experiment is over, praise comments collection one-stop, porcelain!!!!
