TSP problem, also known as traveling salesman problem and salesman problem.
Problem Description: in the given city map, the traveler is required to travel through all cities, and each city can only be visited once, so as to find the shortest path for the traveler to travel through all cities.
Genetic algorithm is used to solve this problem. Genetic algorithm refers to carrying out a limited number of race iterations through a given initial population, and finally making the reserved individuals in the race have the highest fitness (that is, individuals with high fitness can reproduce in the race, and their genes will not be eliminated). Individuals with high fitness represent the required optimal solution.
In this paper, individuals are represented in string form. The individual set uses map < string, integer > population, key: to represent individual chromosomes, and value: to represent individual fitness. Map set is used because it can ensure the uniqueness of individual chromosomes in the population.
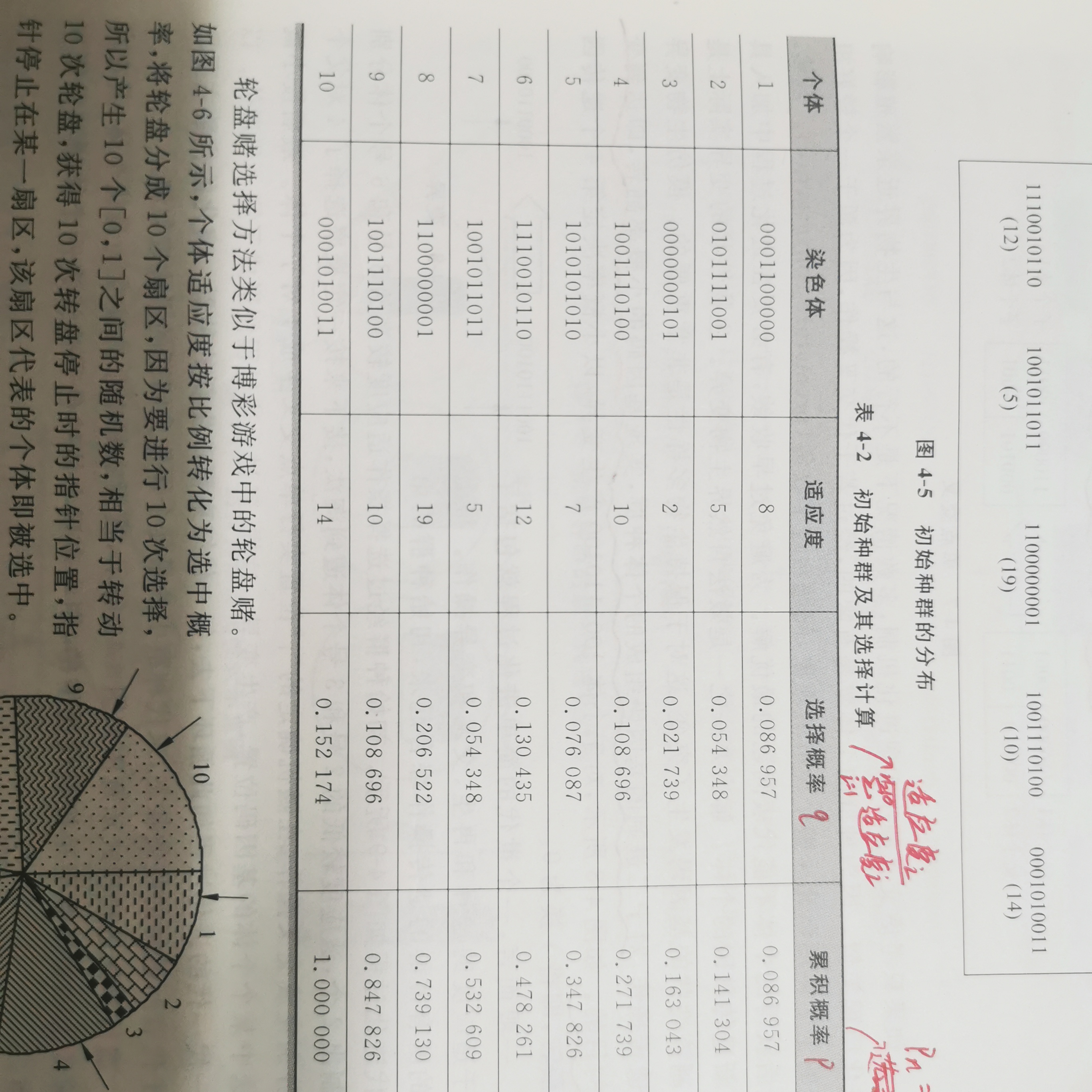
It can be seen from the above figure that the selection probability calculated by individuals with large individual fitness value is also large (selection probability = individual fitness / sum of individual fitness in the population). In TSP problem, the quality of individuals depends on whether the individual distance cost is the smallest. Therefore, in order to ensure the maximum fitness of individuals with small distance cost, a max value is defined (max should be large enough to be greater than the value of the maximum distance cost that may occur in the distance matrix), individual fitness = max individual distance cost . It can ensure that the fitness of individuals with small distance cost is large. Finally, when the optimal solution is output, the minimum distance cost (shortest path length) can be calculated by using max optimal individual fitness.
In the process of population iteration, the following actions are taken:
random_select(Map population): randomly select an individual meeting the probability requirements in the population (in this paper, the individual selected according to this method will be used as the parent to cross breed the offspring)
Reproduction (string x, string y): cross breed according to the selected parent individual to produce a child individual
Mutation (String x): according to the randomly generated probability p (random(0~1)), (if P)< β) The mutation method is to randomly generate two coordinates in the individual, and the coordinate value range is 1~x.length()-1 the subscript 0 cannot be taken here because the starting city can be specified in this method. In order to ensure that subsequent generations take this city as the starting city, it is necessary to ensure that the value of the first bit of the string is not changed in the mutation function and the cross function reproduction.
select_Best(): select the individual with the greatest fitness in the population as the best_individual.
isRepeat (String x): judge the genes that ensure that there are no duplicate genes in an individual's chromosome. In TSP problem, genes refer to the number of cities, chromosomes refer to the way of walking, and each city can only go once. Therefore, it is necessary to ensure that there are no duplicate genes in chromosomes.
*Note: the code in this article cannot guarantee that all the individuals in the final population are the optimal solution individuals (the solution is not yet available, I am a vegetable chicken) , because the population has a variation function, even if there is only one optimal individual in the population in an iterative process, the individual will change due to variation. However, as long as the number of iterations is enough, the optimal solution can appear at least once in the iterative process, and select_best: the solution is saved in the best_individual, so the program can output at last Optimal solution. To output all the optimal solutions, change the best_individual into a Map set, and then control the contents.
package com.AI.Experiment4;
import java.util.*;
/**
* Nodes of genetic algorithm (one node as an individual)
*/
class GN_Node {
public String sol; //Storage path
public int value; //Distance cost of storing the path
public GN_Node(int num){
sol="";
value=Integer.MAX_VALUE;
}
}
/**
* Genetic algorithm to solve TSP problem
*
* Because genetic algorithm requires that individuals with large fitness are easy to reproduce, while TSP problem seeks the shortest path,
* Therefore, it is necessary to ensure that the fitness, selection probability and cumulative probability of the individual with the shortest path value are relatively large
* Therefore, the fitness of individuals is subtracted from the same value (the value should be large enough. It is greater than all available values)
* Can calculate the path length), and then take the absolute value. The final shortest path result only needs
* Use this value to subtract the fitness of the individual.
*/
public class Genetic_algorithms {
private Map<String,Integer> population; //For the population, map is used to save the individual. Key is the gene fragment of the individual and value is the evaluation value of the individual. This can ensure the uniqueness of the individual. A key value pair represents an individual
private int[][] Dist; //Distance matrix of city
private int city_num;//Number of cities
private float mutate;//Individual variation rate (if the probability is less than this number, the variation individual)
private int max=3000; //Maximum
private String best_individual; //Optimal individual
private int best_distance; //Shortest path length
/**
* Initialize various parameters required for algorithm execution
* @param dist City distance matrix
* @param mutate Individual variation rate
* @param start Starting city
* @param num Initialize population size
*/
public Genetic_algorithms(int[][] dist,float mutate,int start,int num){
Dist=dist;
population=new HashMap<>();
city_num=Dist.length;
this.mutate=mutate;
init(start,num);
}
/**
* In the current population, the one with the greatest fitness is selected as the optimal solution
* @return
*/
public void select_Best(){
Set<String> strings = population.keySet();
for (String string : strings) {
if(population.get(string)>best_distance){
best_individual=string;
best_distance=population.get(string);
}
}
}
/**
* Initialize primary population
* @param start Starting city
* @param num Primary population size
*/
public void init(int start,int num){
//Generate an initial population with 10 different individuals
int i=0;
Random random=new Random();//Used to generate an integer between 0~city_num as the city number
do{
String individual=""+start; //Individual, ensure that individual genes are not duplicated. In TSP problem, genes refer to city numbers
for(int j=1;j<city_num;j++){
int gen;
do{
gen=random.nextInt(city_num); //Randomly generated city number
}while(isRepeat(individual,gen));//Ensure that the generated genes are not duplicated
individual+=gen;
}
if(!population.containsKey(individual)){
//If the individual is not included, it is added to the map set
//Calculate the fitness of the individual
int value=evaluate(individual);
population.put(individual,value);
//Initialize the optimal solution and assign the first individual as the optimal solution to best_individual and best_distance
if(i==0){
best_individual=individual;
best_distance=value;
}
i++;
}
}while(i<num);
System.out.println(population);
}
/**
* It is used to check whether a gene is duplicated on the individual gene of the gene
* @return
*/
public boolean isRepeat(String individual,int gen){
for(int i=0;i<individual.length();i++){
if(individual.charAt(i)-'0'==gen)
return true;
}
return false;
}
/**
* To realize individual variation, the variation method is to randomly generate two coordinates, x, y, X ≠ y, and then exchange the genes of X and y
* @param individual
*/
public String mutate(String individual){
Random random=new Random();
int length=individual.length();
int x,y;
do{
x=random.nextInt(length);
y=random.nextInt(length);
}while(!(x!=0&&y!=0&&x!=y));
char[] chars = individual.toCharArray();
char temp=chars[x];
chars[x]=chars[y];
chars[y]=temp;
String mutate_individual="";
for (int i=0;i<chars.length;i++){
mutate_individual+=chars[i];
}
return mutate_individual;
}
/**
* The fitness of the node is calculated according to the incoming individual genes
* @param individual
* @return
*/
public int evaluate(String individual){
int distance=0; //The distance cost is used as the fitness of the individual
int x;
int y;
for(int i=1;i<individual.length();i++){
x=individual.charAt(i-1)-'0'; //Calculate the city number
y=individual.charAt(i)-'0'; //Calculate the city number
distance=distance+Dist[x][y];
}
x=individual.charAt(city_num-1)-'0';
y=individual.charAt(0)-'0';
distance=distance+Dist[x][y];
return -(distance-max);//Because the genetic algorithm requires that individuals with large fitness are easy to reproduce, and the TSP problem seeks the shortest path, the - sign is added to the calculated distance cost to ensure that individuals with small distance cost have large fitness
}
/**
* Individuals were randomly selected to reproduce in the population
* @param population
* @return
*/
public String random_select(Map population){
int sum=0; //Save the sum of individual fitness to calculate the selection probability of individuals. Selection probability = sum of individual fitness / population fitness
Random random=new Random(); //Used to generate random selection probability
Set<String> set = population.keySet();
for (String s : set) {
sum+=(int)population.get(s);
}
for (String s : set) {
double r=random.nextDouble(); //Generate random selection probability
//If the selection probability of the individual is greater than the randomly generated selection probability, the individual will be bred as the selected individual
double value=((double) ((int)population.get(s))/sum);
// System.out.println(r+","+value+","+(int)population.get(s));
if(r<value){
return s;
}
}
return null;
}
/**
* Introduce two parent individuals and put them back into their offspring
* @param x
* @param y
* @return
*/
public String reproduce(String x,String y){
int n=x.length();
Random random=new Random(); //Used to generate random segmentation points, but cannot go to 0 and n-1
int index=0;
do{
index=random.nextInt(n);
}while(index>0&&index<n-1);
return x.substring(0,index)+y.substring(index,n); //Return offspring
}
/**
* Determine whether there are duplicate genes
* @param individual
* @return
*/
public boolean isRepeat(String individual){
for(int i=0;i<individual.length();i++){
for(int j=i+1;j<individual.length();j++){
if(individual.charAt(i)==individual.charAt(j))
return true;
}
}
return false;
}
/**
* Main function of genetic algorithm
*
*/
public void GN_main(){
Random random=new Random();
int num_iteration=0; //Count the number of iterations of the population
while(num_iteration<10000){
Map<String,Integer> new_population=new HashMap<>(); //Temporary storage of newly generated populations
//In each iteration, the best_individual is selected from the population
select_Best();
for(int i=0;i<population.size();i++){
//Select two parents at random
String parent1;
String parent2;
do {
parent1=random_select(population);
}while (parent1==null);
do {
parent2=random_select(population);
}while (parent2==null);
//Two parents produce one child to ensure that there are no duplicate genes in the offspring
String child;
do {
child=reproduce(parent1,parent2);
}while (isRepeat(child));
float r=random.nextFloat(); //Randomly generate a number between 0 and 1
if(r<random.nextFloat()){
child=mutate(child);
}
if(!new_population.containsKey(child)){
int value=evaluate(child);
new_population.put(child,value); //Adding offspring to the population
}
}
//Update the population, take the newly generated population as the current population and continue to breed the next generation
population=new_population;
/*
Here is an idea: we want to carry out an elimination mechanism in the population, combine the new species in the population, and then calculate the average fitness of the population,
Then, the individuals whose fitness is less than the average fitness in the merged population are eliminated from the population. In order to ensure that the population continues to converge to the optimal individual (i.e. the desired population)
The remaining individuals are the optimal solution), but the program logic feels no problem, but the program reports an error
(Exception in thread "main" java.util.ConcurrentModificationException)
I don't understand why I reported an error.....
Set<String> strings = new_population.keySet();
for (String string : strings) {
if (!population.containsKey(string)){
population.put(string,new_population.get(string));
}
}
System.out.println(population);
//Eliminate some members of the population where the fitness is lower than the average
Set<String> strings1 = population.keySet();
int sum=0;
for (String s : strings1) {
sum+=population.get(s);
}
sum=sum/population.size();
for (String s : strings1) { //Error location!!!!!!!!!!!!!!!!
if(population.get(s)<=sum){
population.remove(s);
}
}
*/
num_iteration++;
System.out.println("Current iteration No"+num_iteration+"Times. Race:"+population);
}
}
public String getBest_individual() {
return best_individual;
}
public int getBest_distance() {
return best_distance;
}
public Map<String, Integer> getPopulation() {
return population;
}
public static void main(String[] args) {
int max=655;
//Distance matrix
int[][] Dist={{max,3,2,3,max},{3,max,max,6,4},{2,max,max,1,5},{3,6,1,max,7},{max,4,5,7,max}};
float a=0.98f;
Genetic_algorithms sa=new Genetic_algorithms(Dist,a,0,10);
sa.GN_main();
System.out.println("Optimal driving path:"+sa.getBest_individual()+".Shortest path:"+(3000-sa.getBest_distance()));
}
}
If you have any questions or suggestions about this article, please leave a message in the comment area.