Recently, several friends are asking about the ambiguity fixing method in rtklib. I have sorted out the questions and answered them here. If there are other questions or unclear points, we can discuss them again.

Ambiguity resolution method

Select the ambiguity mode through the interface

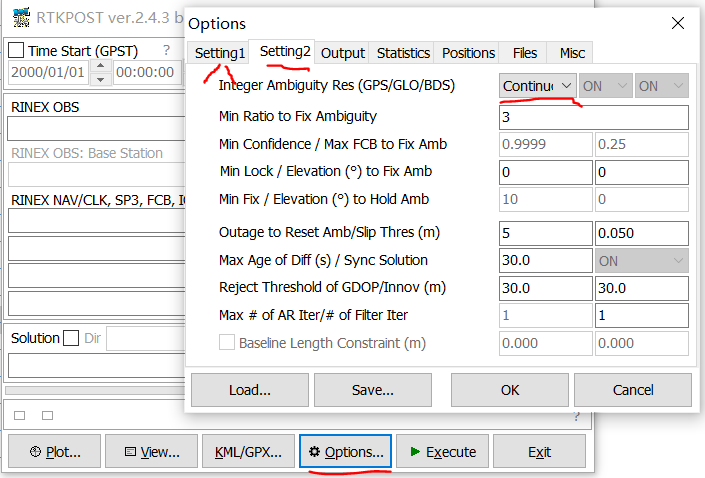
If we are only users of rtklib (no further secondary development or research based on its source code, only data solution and verification, etc.). Then we can select the ambiguity fixing method in the following position, rtklib_ bin-rtklib_ 2.4.3 \ bin > rtkpost. Exe > Options > setting2 > integer ambiguity res. of course, we should set the positioning mode as one of the high-precision solutions in setting1, and this option can be selected (this is reasonable, and it is meaningful only to fix the integer ambiguity of the solution based on the carrier phase)

Set ambiguity mode through code

If we need to study its code, we will find the macro definition of ambiguity resolution mode in \ rtklib\rtklib.h

#define ARMODE_OFF  0                   /* AR mode: off */
#define ARMODE_CONT 1                   /* AR mode: continuous */
#define ARMODE_INST 2                   /* AR mode: instantaneous */
#define ARMODE_FIXHOLD 3                /* AR mode: fix and hold */
#define ARMODE_WLNL 4                   /* AR mode: wide lane/narrow lane */
#define ARMODE_TCAR 5                   /* AR mode: triple carrier ar */

When we need high-precision solution, in most cases, we call postpos, which has a parameter const prcopt of structure pointer type_ T * popt, there is a variable modear in this structure, and the ambiguity mode is set through this variable.

typedef struct {        /* processing options type */
   ...
    int modear;         /* AR mode (0:off,1:continuous,2:instantaneous,3:fix and hold,4:ppp-ar) */
    ...  
} prcopt_t;

/* post-processing positioning -----------------------------------------------*/
EXPORT int postpos(gtime_t ts, gtime_t te, double ti, double tu,
                   const prcopt_t *popt, const solopt_t *sopt,
                   const filopt_t *fopt, char **infile, int n, char *outfile,
                   const char *rov, const char *base);

Introduction of various modes

WLNL and TCAR

These are two fuzzy solutions corresponding to the lambda algorithm. Previously, two function interfaces were reserved in rtkpos.c. now they have been removed from the code, and the two macros below have been retained, but they are not used in the code, so we don't need to care

#define ARMODE_WLNL 4                   /* AR mode: wide lane/narrow lane */
#define ARMODE_TCAR 5                   /* AR mode: triple carrier ar */

ARMODE_OFF

As the name suggests, the ambiguity is not fixed in this ambiguity mode. The code below is from rtkpos.c. It can be seen that we will not fix the ambiguity in the following three cases,

• positioning mode refers to single point positioning or pseudo range difference
• The blur mode is set to off
• The threshold value of ratio is less than 1. It is meaningless to set the threshold value of ratio to a value less than 1, because the value we calculate is always greater than 1

/* resolve integer ambiguity by LAMBDA ---------------------------------------*/
static int resamb_LAMBDA(rtk_t *rtk, double *bias, double *xa)
{
...    
    if (rtk->opt.mode<=PMODE_DGPS||rtk->opt.modear==ARMODE_OFF||
        rtk->opt.thresar[0]<1.0) {
        return 0;
    }
    ...
}

Instantaneous

This mode can be understood as an independent solution mode. We separate the relationship between fuzziness in different epochs. For the solution of each epochs, we return all the state quantities corresponding to fuzziness to 0. The code below comes from the time update part of fuzziness state udbias

if (rtk->opt.modear==ARMODE_INST&&rtk->x[IB(i,k,&rtk->opt)]!=0.0) {
                initx(rtk,0.0,0.0,IB(i,k,&rtk->opt));
            }

continuous

Continuous mode. We can't find the use of this mode in the code, which is reasonable. This mode has an opposite relationship with instant. In this case, we don't return the corresponding state quantity to 0 when updating the ambiguity of the new epoch

fix and hold - blur hold

If we set the hold mode, first of all, we are not an independent solution mode, so the ambiguity will not return to 0 in each epoch. In addition, this mode has another use - ambiguity maintenance. We can see that when our fixed number of epochs reaches the set threshold and the solution mode is ambiguity preserving, we will enter the holdamb function. So what is ambiguity preserving? Is the ambiguity unchanged once it is fixed? Of course not.

 /* hold integer ambiguity */
                if (++rtk->nfix>=rtk->opt.minfix&&
                    rtk->opt.modear==ARMODE_FIXHOLD) {
                    holdamb(rtk,xa);
                }

How is ambiguity maintained

To understand the ambiguity preserving function, we must understand kalman filtering. If we don't understand Karaman filtering algorithm, it won't work. rtklib's floating-point solution is solved by Karaman filter, so you know. Below is the code in holdamb, simply add a few lines of comments.

        /* constraint to fixed ambiguity */
        for (i=1;i<n;i++) {
            /* We use the existing ambiguity as the observation measure */
            v[nv]=(xa[index[0]]-xa[index[i]])-(rtk->x[index[0]]-rtk->x[index[i]]);
            /* Here is the setting of the observation matrix */
            H[index[0]+nv*rtk->nx]= 1.0;
            H[index[i]+nv*rtk->nx]=-1.0;
            nv++;
        }
    }
    if (nv>0) {
        R=zeros(nv,nv);
        /* Here is the setting of observation noise, which is written dead in rtklib */
        for (i=0;i<nv;i++) R[i+i*nv]=VAR_HOLDAMB;
        
        
        /* Here, the measurement update of kalman filter is carried out */
        if ((info=filter(rtk->x,rtk->P,H,v,R,rtk->nx,nv))) {

test result

(generating, please wait...)