Today, when compiling a project, we need to get "the theme matching of a movie that an actor is good at", the first thought is the association algorithm, and then think that the support index of Apriori algorithm meets this requirement very well.

As long as we find the film theme matching that meets the "minimum support index", we can meet the needs of the project.

1. Look at the data at hand first

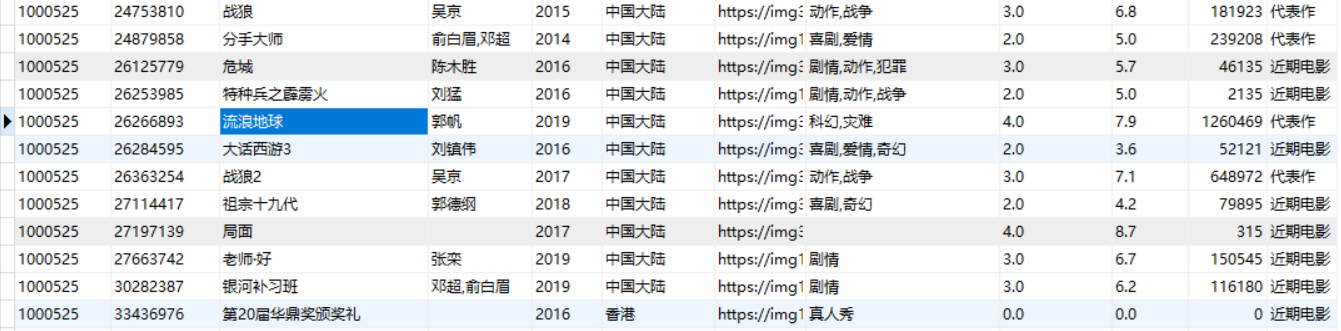
Each actor has many movies, and each movie has many themes. Only a single actor needs to be analyzed in the project.

2. Find out all the movies of an actor and integrate them.

public List getPreferGenres(String actorId) {
          List<Movie> movieList = movieRepository.findMovieByActorId(actorId);
          List<List<String>> genresList = new ArrayList<>();
          for (Movie movie : movieList) {
               List genres = new ArrayList();
               String movieGenres = movie.getGenres();
               //Filter out theme-free movies and reality shows
               if (movieGenres.equals("")|| movieGenres.equals("Reality show"))
                    continue;
               genres = Arrays.asList(movieGenres.split(","));
               genresList.add(genres);
          }
          return AprioriUtil.getPreferGenres(genresList);
     }

The subject matter of each movie is stored in a List, which is also stored in a large List. OK, the data is sorted out and comes to Apriori Util.

3. Output of raw data

//******************* Read Data Set************************************
        record = genresList;
        System.out.println("Reading Data Sets in Matrix Form record");
        for(int i=0;i<record.size();i++){
            List<String> list= new ArrayList<String>(record.get(i));
            for(int j=0;j<list.size();j++){
                System.out.print(list.get(j)+" ");
            }
            System.out.println();
        }

Read data sets
Action war
Comedy Love
Plot action crime
Plot action war
Sci-fi disaster
Comedy Love Fantasy
Action war
Comedy Fantasy
Plot
Plot

The output results are consistent with those in the database.

4. Get a candidate set

Candidate 1 itemset is a list of all elements in the set. In order not to repeat, HashSet is used as a medium.

private static List<List<String>> findFirstCandidate() {
        List<List<String>> tableList = new ArrayList<>();
        HashSet hashSet = new HashSet();
        for (int i = 0;i<record.size();i++){
            List list = record.get(i);
            for (int j = 0;j<list.size();j++){
                hashSet.add(list.get(j));
            }
        }
        Iterator iterator = hashSet.iterator();
        while (iterator.hasNext()){
            List tempList = new ArrayList();
            tempList.add(iterator.next());
            tableList.add(tempList);
        }
        return tableList;
    }

Print candidate 1 item set (code similar to previous print code)

Candidate 1 Item Set
Comedy
Plot
Crimes
Science fiction
Love
War
Action
Disaster
Fantasy

Consistent with expected results

5. Pruning candidate itemsets - > frequent itemsets

private static List<List<String>> getSupprotedItemset(List<List<String>> candidateItemset) {
        boolean end = true;
        List<List<String>> supportedItemset = new ArrayList<List<String>>();
        int k = 0;
        for (int i = 0;i<candidateItemset.size();i++){
            int count  = countFrequent(candidateItemset.get(i));//Statistical records
            if (count >= MIN_SUPPORT*record.size()){
                supportedItemset.add(candidateItemset.get(i));
                end = false;
            }
        }
        endTag = end;
        if(endTag==true)
            System.out.println("Unsatisfactory support itemsets,End the connection");
        return supportedItemset;
    }

The basis of pruning is the minimum support, which will be eliminated when the theme combination does not meet the minimum support (that is, the proportion of the total number of movies is less than the minimum support). The minimum support can be set at (0,1) and the project is set at 0.2.

Print frequent itemsets

Frequent Item Set
Comedy
Plot
Love
War
Action
Fantasy
Consistent with expected results

6. Frequent 1 Item Set - > Candidate 2 Item Sets

All items in the candidate 2 sets satisfy the following conditions:

2 themes

From Frequent Item Set

Is an item (or subset) in the original data

private static List<List<String>> getNextCandidate(List<List<String>> frequentItemset) {
        List<List<String>> nextCandidateItemset = new ArrayList<List<String>>();
        for (int i = 0; i<frequentItemset.size();i++){
            List tempList = frequentItemset.get(i);
            HashSet hashSet = new HashSet();
            HashSet tempHashSet = new HashSet();
            for (int j = 0;j<tempList.size();j++){
                hashSet.add(tempList.get(j));
            }
            int beforeSize = hashSet.size();
            tempHashSet = (HashSet) hashSet.clone();
            for (int k = i+1;k<frequentItemset.size();k++){
                hashSet = (HashSet)tempHashSet.clone();
                for (int m = 0;m<frequentItemset.get(k).size();m++){
                    hashSet.add(frequentItemset.get(k).get(m));
                }
                int afterSize = hashSet.size();
                if(afterSize == beforeSize+1 && isSubsetOf(hashSet,record)==1 && isnotHave(hashSet,nextCandidateItemset)){
                    Iterator<String> itr = hashSet.iterator();
                    List<String>  temphsList = new ArrayList<String>();
                    while(itr.hasNext()){
                        String Item = (String) itr.next();
                        temphsList.add(Item);
                    }
                    nextCandidateItemset.add(temphsList);
                }
            }

        }
        return  nextCandidateItemset;
    }

Combination algorithm idea: from the first item of the frequent I item set, the frequent I item set is scanned, and the new item is obtained by combining the current item with one element of the other item. If the new item satisfies the following conditions, a candidate i+1 itemset is added:

There is i+1 element in the new item (meaning that the element in the current item cannot be duplicated with "one element";

The new item is the item (or subset) of the original data;

Candidate i+1 item set is not added to the new item (new item can not be added repeatedly);

Output of candidate i+1 itemsets

Scanning backup
Comedy Love
Comedy Fantasy
Plot war
Plot action
Love Fantasy
War action

Satisfying expected results

7. Repeat iterations from step 5 until the final combination does not meet the minimum support.

Iterative process output (followed by step 6 output)

Frequent set after scanning
Comedy Love
Comedy Fantasy
Plot action
War action
Scanning backup
Comedy Love Fantasy
Plot war action
End the connection without satisfying the support itemset
Frequent set after scanning
Apriori algorithm result set
Comedy Love
Comedy Fantasy
Plot action
War action
Meeting expected results

Complete the whole algorithm process.