This paper is a study note of data structure of Zhejiang University.
Heap is also known as priority queue. The entry and exit of elements in the queue are based on the principle of first in first out, while in the heap, the priority of elements is taken out according to the size.
The most commonly used structure of a heap is represented by a binary tree, usually a complete binary tree. Because of the extremely regular arrangement of nodes in the complete binary tree, it can be directly stored in an array.
Thus, the heap has two characteristics:
1. Structural characteristics: the complete binary tree is represented by an array;
2. Partial ordering: the value of any node element is related to the value stored by its child nodes.
There are two basic types of heaps: MinHeap and MaxHeap. In the former, the value of any node is greater than or equal to the value of its child nodes; in the latter, the value of any node is less than or equal to the value of its child nodes.
Here is just an example of the operation of the largest heap.
1. Structure definition of heap
struct Heap { ElementType *Data; int Size; //Mark the current number of elements int Capacity; //Mark maximum capacity }; typedef Heap MaxHeap; typedef Heap MinHeap;
2. Initialize the heap
/*Initialization reactor*/ MaxHeap *InitiateHeap(int MaxSize) { MaxHeap *H=new MaxHeap; H->Data=new ElementType[MaxSize+1]; H->Size=0; H->Capacity=MaxSize; H->Data[0]=MAXDATE; return(H); }
3. Judge the pile
/*Judgment stack*/ bool IsFull(MaxHeap *H) { return(H->Size==H->Capacity); }
4. Judge the pile empty
/*Judge heap space*/ bool IsEmpty(MaxHeap *H) { return(H->Size==0); }
5. Insert element X in the heap
/*Insert X in Max heap*/ void Insert(MaxHeap *H,ElementType X) { int i; if(IsFull(H)){ cout<<"Heap full"<<endl; return; } i=++H->Size; //i points to the location of the new element for(;H->Data[i/2]<X;i/=2) H->Data[i]=H->Data[i/2]; //Move element X up where it is inserted H->Data[i]=X; }
6. Take out the element with the maximum key value and delete a node
/*Remove the element with the maximum key value and delete a node*/ ElementType DeleteMax(MaxHeap *H) { int Parent,Child; ElementType MaxItem,X; if(IsEmpty(H)){ cout<<"Heap empty"<<endl; return ERROR; } MaxItem=H->Data[1]; X=H->Data[H->Size--]; for(Parent=1;Parent*2<=H->Size;Parent=Child){ //Cycle condition: judge whether the left son exists Child=Parent*2; //Child points to his left son if((Child!=H->Size) && (H->Data[Child]<H->Data[Child+1])) //The right son exists, and the right son is older than the left son Child++; if(X>=H->Data[Child]) break; else H->Data[Parent]=H->Data[Child]; //Move element X down } H->Data[Parent]=X; return(MaxItem); }
7. Adjust the existing heap to the maximum heap: 1. First ensure the structural characteristics (complete binary tree); 2. Adjust the order
/*Adjust the existing heap to the maximum heap: 1. First ensure the structural characteristics (complete binary tree); 2. Adjust the order*/ void BuildHeap(MaxHeap *H) { int i; for(i=H->Size/2;i>0;i--) //Starting from the last parent node PercDown(H,i); }
PercDown() function
/*Adjust the sub heap with H - > data [P] as root in H to the maximum heap*/ void PercDown(MaxHeap *H,int p) { int Parent,Child; ElementType X; X=H->Data[p]; for(Parent=p;Parent*2<=H->Size;Parent=Child){ Child=Parent*2; if((Child!=H->Size)&&(H->Data[Child]<H->Data[Child+1])) Child++; if(X>=H->Data[Child]) break; else H->Data[Parent]=H->Data[Child]; } H->Data[Parent]=X; }
A complete program to run:
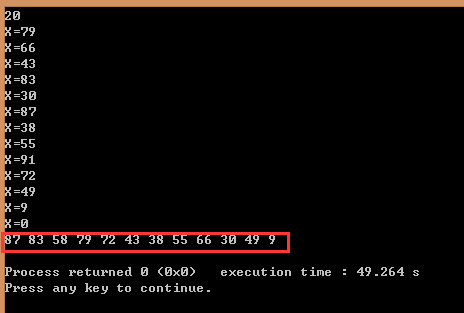
Create a maximum heap based on the input elements, insert a value of 58, delete the largest elements in the heap, and print out all elements in the heap.
#include <iostream> #define MAXDATE 100 #define ERROR -1; using namespace std; typedef int ElementType; struct Heap { ElementType *Data; int Size; //Mark the current number of elements int Capacity; //Mark maximum capacity }; typedef Heap MaxHeap; typedef Heap MinHeap; int main() { MaxHeap *InitiateHeap(int MaxSize); void Insert(MaxHeap *H,ElementType X); void BuildHeap(MaxHeap *H); ElementType DeleteMax(MaxHeap *H); int MaxSize; cin>>MaxSize; MaxHeap *H; H=InitiateHeap(MaxSize); ElementType X; cout<<"X="; cin>>X; while(X!=0){ H->Data[++H->Size]=X; cout<<"X="; cin>>X; } BuildHeap(H); Insert(H,58); DeleteMax(H); int i; for(i=1;i<=H->Size;i++) cout<<H->Data[i]<<' '; cout<<endl; return 0; } /*Initialization reactor*/ MaxHeap *InitiateHeap(int MaxSize) { MaxHeap *H=new MaxHeap; H->Data=new ElementType[MaxSize+1]; H->Size=0; H->Capacity=MaxSize; H->Data[0]=MAXDATE; return(H); } /*Judgment stack*/ bool IsFull(MaxHeap *H) { return(H->Size==H->Capacity); } /*Judge heap space*/ bool IsEmpty(MaxHeap *H) { return(H->Size==0); } /*Insert X in Max heap*/ void Insert(MaxHeap *H,ElementType X) { int i; if(IsFull(H)){ cout<<"Heap full"<<endl; return; } i=++H->Size; //i points to the location of the new element for(;H->Data[i/2]<X;i/=2) H->Data[i]=H->Data[i/2]; //Move element X up where it is inserted H->Data[i]=X; } /*Remove the element with the maximum key value and delete a node*/ ElementType DeleteMax(MaxHeap *H) { int Parent,Child; ElementType MaxItem,X; if(IsEmpty(H)){ cout<<"Heap empty"<<endl; return ERROR; } MaxItem=H->Data[1]; X=H->Data[H->Size--]; for(Parent=1;Parent*2<=H->Size;Parent=Child){ //Cycle condition: judge whether the left son exists Child=Parent*2; //Child points to his left son if((Child!=H->Size) && (H->Data[Child]<H->Data[Child+1])) //The right son exists, and the right son is older than the left son Child++; if(X>=H->Data[Child]) break; else H->Data[Parent]=H->Data[Child]; //Move element X down } H->Data[Parent]=X; return(MaxItem); } /*Adjust the sub heap with H - > data [P] as root in H to the maximum heap*/ void PercDown(MaxHeap *H,int p) { int Parent,Child; ElementType X; X=H->Data[p]; for(Parent=p;Parent*2<=H->Size;Parent=Child){ Child=Parent*2; if((Child!=H->Size)&&(H->Data[Child]<H->Data[Child+1])) Child++; if(X>=H->Data[Child]) break; else H->Data[Parent]=H->Data[Child]; } H->Data[Parent]=X; } /*Adjust the existing heap to the maximum heap: 1. First ensure the structural characteristics (complete binary tree); 2. Adjust the order*/ void BuildHeap(MaxHeap *H) { int i; for(i=H->Size/2;i>0;i--) //Starting from the last parent node PercDown(H,i); }
Operation result (output in red box):