And maximum string (C language)

Reference blog: https://www.cnblogs.com/activeshj/p/4090817.html

Problem description

Give you an integer array, in which the elements have positive, negative and 0. You are required to find a continuous substring. The sum of all elements of the substring is the largest of all continuous substrings.

Example: given a set of numbers, n, positive and negative. It is required to find and the largest continuous substring, such as:

5 ， 4， -10， 11， 2， 8， -5， 4， 2，-3，1

It can be determined that the largest continuous substring is 11, 2, 8, - 5, 4, 2, and the sum is 22.

Algorithm idea

• If we use the brute force method, we can find all the strings (find the starting point in two cycles), and then compare the size (add the sum in another cycle, and compare it with the previous maximum sum). In this way, the complexity of the algorithm is O(n^3)

We can change the idea to make the algorithm complexity O(n):

Assuming that the largest substring Maxpre from 0 to i-1 has been found, now we need to deal with the situation after adding element i.

There are two possibilities: the largest substring is the largest substring from 0 to i-1, which is recorded as Maxpre; The maximum substring should contain element i, which is recorded as Maxcur.

Compare Maxpre with Maxcur, assign a large value to Maxpre, and continue scanning until the last element is processed, thus forming an O(n) algorithm.

Train of thought details

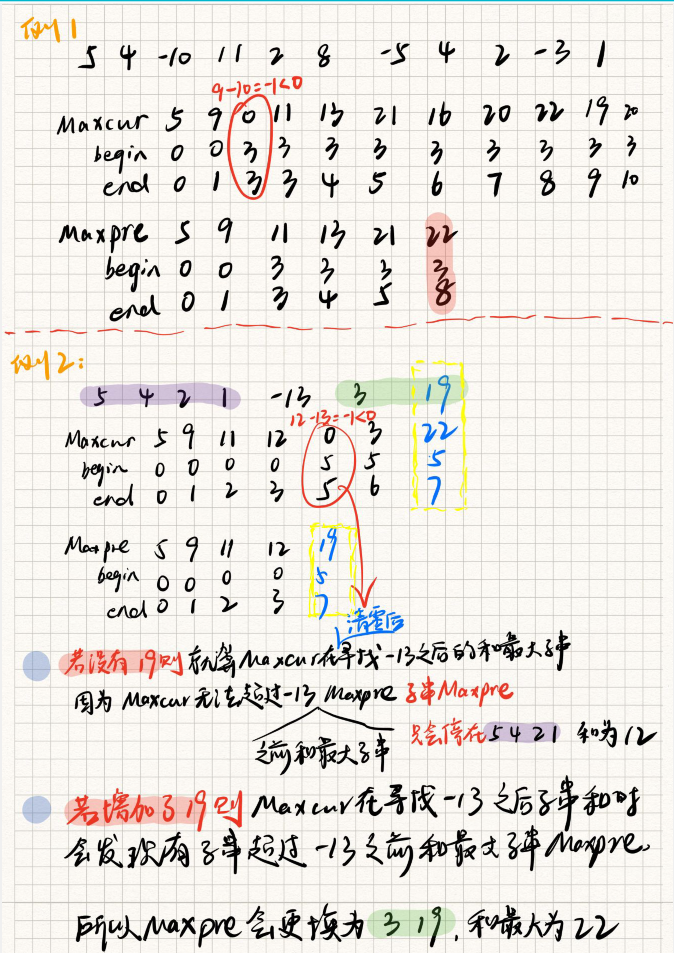
We first set the values of Maxcur and Maxpre to 0, and their starting subscripts to 0.

Then, first assign a value to Maxcur through a layer of for loop (the maximum substring should contain element i, which is recorded as Maxcur).

• If the sum of Maxcur plus a[i] > = 0, it means that the end index of Maxcur substring can continue to go back (because (the number immediately following)+
  The previous substring with a sum ≥ 0) will only ≥
  But this does not mean that the indexes of Maxcur's begin and end are the current maximum string of 0-i (because it is also compared with the maximum substring Maxpre from 0 to i-1, which may not contain a[i])
• If the sum of Maxcur plus a[i] is < 0. Note: including this a[i] will make the following number + the sum substring of the previous Maxcur record certain to change<
  Therefore, if we want to find the largest substring, the previous one can be discarded. At this time, Maxcur must be cleared at i, and the index continues to find the substring from i+1. Note: after clearing, Maxcur will
  < Maxpre, indicating that the Maxpre after clearing still retains the previous 0-i and the largest substring (and the substring does not include a[i]).

//MaxCur reset
MaxCur = 0;
MaxCurIdx.begin = i + 1;
MaxCurIdx.end = i + 1;

Graphical thinking

code implementation

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 11

typedef struct subIdx {
    int begin;
    int end;
} SUB_IDX;

typedef struct maxSub {
    SUB_IDX subPosition;
    int sum;
} MAX_SUB;

MAX_SUB * MaxSubScan(const int* array, int len)
{
    SUB_IDX MaxPreIdx;
            MaxPreIdx.begin = 0;
            MaxPreIdx.end = 0;
    SUB_IDX MaxCurIdx;
            MaxCurIdx.begin = 0;
            MaxCurIdx.end = 0;
    int MaxPre = 0;
    int MaxCur = 0;
    int i;

    for (i = 0 ; i < len; i++) {
        if ((MaxCur + array[i]) > 0) {
            MaxCur = MaxCur + array[i];
            MaxCurIdx.end = i;
        } else {
            MaxCur = 0;
            MaxCurIdx.begin = i + 1;
            MaxCurIdx.end = i + 1;
        }

        if (MaxCur > MaxPre) {
            MaxPre = MaxCur;
            MaxPreIdx.begin = MaxCurIdx.begin;
            MaxPreIdx.end = MaxCurIdx.end;
        }
    }

    MAX_SUB *maxsub = (MAX_SUB *) malloc( sizeof(MAX_SUB) );
    maxsub->subPosition.begin = MaxPreIdx.begin;
    maxsub->subPosition.end = MaxPreIdx.end;
    maxsub->sum = MaxPre;

    return maxsub;
}

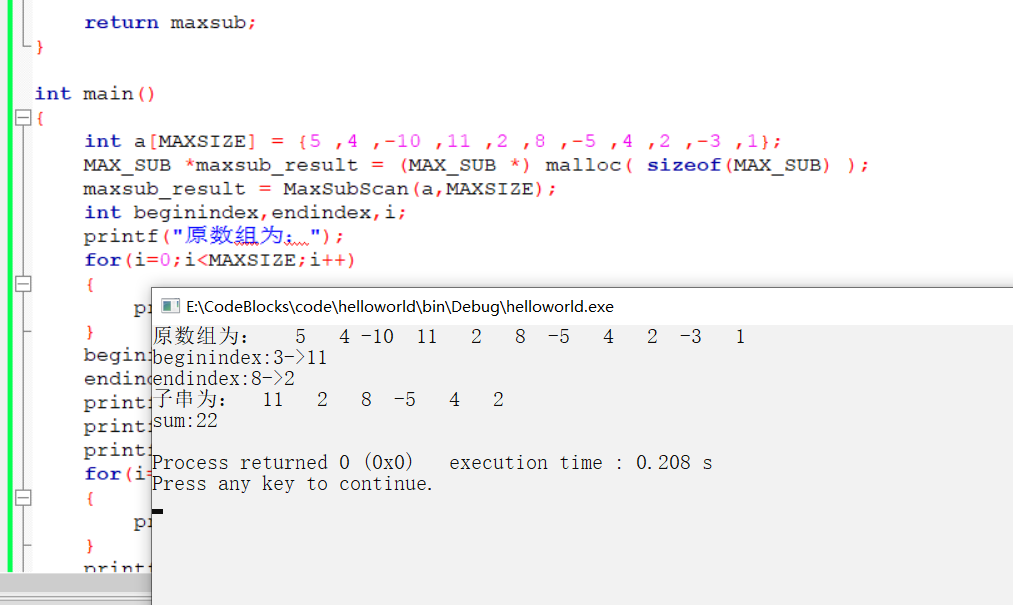
int main()
{
    int a[MAXSIZE] = {5 ,4 ,-10 ,11 ,2 ,8 ,-5 ,4 ,2 ,-3 ,1};
    MAX_SUB *maxsub_result = (MAX_SUB *) malloc( sizeof(MAX_SUB) );
    maxsub_result = MaxSubScan(a,MAXSIZE);
    int beginindex,endindex,i;

    beginindex = maxsub_result->subPosition.begin;
    endindex = maxsub_result->subPosition.end;
    printf("beginindex:%d->%d\n",beginindex,a[beginindex]);
    printf("endindex:%d->%d\n",endindex,a[endindex]);
    printf("Substrings are:");
    for(i=beginindex;i<endindex+1;i++)
    {
        printf("%4d",a[i]);
    }
    printf("\nsum:%d\n",maxsub_result->sum);

}

screenshot