Analysis of DES encryption and decryption algorithm
Summary
DES is a group encryption algorithm, which encrypts data in 64 bits. DES is also a symmetric algorithm: encryption and decryption use the same algorithm. DES is a 16 stage "replace replace replace" block cipher algorithm. The 64 bit block plaintext sequence is the input of the encryption algorithm. After 16 rounds of encryption, the 64 bit ciphertext sequence is obtained.
See the following figure for algorithm principle:
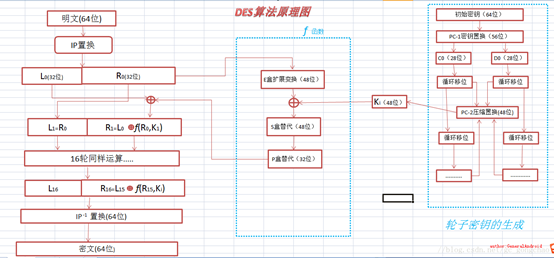
Principle analysis
DES algorithm is mainly divided into three parts: encryption and decryption operation, f function processing, wheel key generation, from right to left are briefly introduced.
Generation of wheel key
Data sheet 1
//PC-1
private int[] PC1={57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,23,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4};
//PC-2
private int[] PC2={14,17,11,24,1,5,3,28,
15,6,21,10,23,19,12,4,
26,8,16,7,27,20,13,2,
41,52,31,37,47,55,30,40,
51,45,33,48,44,49,39,56,
34,53,46,42,50,36,29,32};
//Schedule of Left Shifts
private int[] LFT={1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1};
The generation of 16 subkeys mainly uses the data table in data table 1. Firstly, the 64 bit initial key is compressed by PC1 to replace the 56 bit key, and then it is divided into two parts, which are recorded as C0 and D0. Here, C0 of 28 bits and D0 of 28 bits are shifted to the left according to the corresponding position of LET array to get C1 and D1. This is to combine C1 and D1 to compress and displace according to PC2 to obtain 48 bit sub key, and note that C1 and D1 are used as input of next round to generate next sub key.
Operation of f function
Data sheet 2
//E extension
private int[] E={32,1,2,3,4,5,
4,5,6,7,8,9,
8,9,10,11,12,13,
12,13,14,15,16,17,
16,17,18,19,20,21,
20,21,22,23,24,25,
24,25,26,27,28,29,
28,29,30,31,32,1};
/ / P replacement
private int[] P={16,7,20,21,29,12,28,17,
1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,
19,13,30,6,22,11,4,25};
Private static final int [] [] [] S-box = {/ / S-box
{// S_Box[1]
{ 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7 },
{ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8 },
{ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0 },
{ 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 } },
{ // S_Box[2]
{ 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10 },
{ 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5 },
{ 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15 },
{ 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 } },
{ // S_Box[3]
{ 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8 },
{ 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1 },
{ 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7 },
{ 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 } },
{ // S_Box[4]
{ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15 },
{ 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9 },
{ 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4 },
{ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 } },
{ // S_Box[5]
{ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9 },
{ 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6 },
{ 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14 },
{ 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 } },
{ // S_Box[6]
{ 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11 },
{ 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8 },
{ 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6 },
{ 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 } },
{ // S_Box[7]
{ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 },
{ 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6 },
{ 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2 },
{ 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 } },
{ // S_Box[8]
{ 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7 },
{ 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2 },
{ 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8 },
{ 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 } }
};
As can be seen from the schematic diagram, the input of f function is that the right half of plaintext packet is recorded as R and the sub key is recorded as K. 32-bit r first uses E in data table 2 to perform E-box expansion transformation to obtain 48 bit data, which is recorded here as RE. Then RE and K are XOR operated and the XOR result is replaced by S box in data table 2. The result of 48 bit operation is recorded as rs. Then RS uses P in data table 2 to replace P box, and the final result of 32 bits is recorded as RF. Here, the operation task of f function is completed.
Encryption and decryption operation
//Initial replacement
private int[] IP={58,50,42,34,26,18,10,2,
60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,
64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,
59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,
63,55,47,39,31,23,15,7};
/ / inverse initial displacement
private int[] IP_1={40,8,48,16,56,24,64,32,
39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,
37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,
35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58,26,
33,1,41,9,49,17,57,25};
In the first round, the 64 bit plaintext is divided into L0 and R0, and the encryption operation is as follows:
L1=R0
R1=L0⊕f(R0,K0)
Then 16 rounds of operation are performed according to the formula.
code implementation
CustomDES
package com.lcx.des; public class CustomDES { //Initial permutation private int[] IP = {58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4, 62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8, 57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3, 61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7}; //Inverse initial permutation private int[] IP_1 = {40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31, 38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29, 36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27, 34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25};//The array data is incomplete //E extension private int[] E = {32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17, 16, 17, 18, 19, 20, 21, 20, 21, 22, 23, 24, 25, 24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1}; //P replacement private int[] P = {16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10, 2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4, 25}; private static final int[][][] S_Box = { { {14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7}, {0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8}, {4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0}, {15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13}}, { {15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10}, {3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5}, {0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15}, {13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9}}, { {10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8}, {13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1}, {13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7}, {1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12}}, { {7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15}, {13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9}, {10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4}, {3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14}}, { {2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9}, {14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6}, {4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14}, {11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3}}, { {12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11}, {10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8}, {9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6}, {4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13}}, { {4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1}, {13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6}, {1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2}, {6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12}}, { {13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7}, {1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2}, {7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8}, {2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11}} }; //PC-1 private int[] PC1 = {57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18, 10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36, 63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22, 14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4}; //PC-2 private int[] PC2 = {14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10, 23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2, 41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48, 44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32}; //Schedule of Left Shifts private int[] LFT = {1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1}; /** * Number of encryption rounds **/ private static final int LOOP_NUM = 16; private String[] keys = new String[LOOP_NUM]; private String[] pContent; private String[] cContent; private int origin_length; /** * 16 Subkey **/ private int[][] sub_key = new int[16][48]; private String content; private int p_origin_length; public CustomDES(String key, String content) { this.content = content; p_origin_length = content.getBytes().length; generateKeys(key); } /****Split group****/ public byte[] deal(byte[] p, int flag) { origin_length = p.length; int g_num; int r_num; g_num = origin_length / 8; r_num = 8 - (origin_length - g_num * 8);//8 no filling byte[] p_padding; /****Fill********/ if (r_num < 8) { p_padding = new byte[origin_length + r_num]; System.arraycopy(p, 0, p_padding, 0, origin_length); for (int i = 0; i < r_num; i++) { p_padding[origin_length + i] = (byte) r_num; } } else { p_padding = p; } g_num = p_padding.length / 8; byte[] f_p = new byte[8]; byte[] result_data = new byte[p_padding.length]; for (int i = 0; i < g_num; i++) { System.arraycopy(p_padding, i * 8, f_p, 0, 8); System.arraycopy(descryUnit(f_p, sub_key, flag), 0, result_data, i * 8, 8); } if (flag == 0) {//Decrypt byte[] p_result_data = new byte[p_origin_length]; System.arraycopy(result_data, 0, p_result_data, 0, p_origin_length); return p_result_data; } return result_data; } /** * encryption **/ public byte[] descryUnit(byte[] p, int k[][], int flag) { int[] p_bit = new int[64]; StringBuilder stringBuilder = new StringBuilder(); for (int i = 0; i < 8; i++) { String p_b = Integer.toBinaryString(p[i] & 0xff); while (p_b.length() % 8 != 0) { p_b = "0" + p_b; } stringBuilder.append(p_b); } String p_str = stringBuilder.toString(); for (int i = 0; i < 64; i++) { int p_t = Integer.valueOf(p_str.charAt(i)); if (p_t == 48) { p_t = 0; } else if (p_t == 49) { p_t = 1; } else { System.out.println("To bit error!"); } p_bit[i] = p_t; } /***IP Replacement * **/ int[] p_IP = new int[64]; for (int i = 0; i < 64; i++) { p_IP[i] = p_bit[IP[i] - 1]; } if (flag == 1) { // encryption for (int i = 0; i < 16; i++) { L(p_IP, i, flag, k[i]); } } else if (flag == 0) { // Decrypt for (int i = 15; i > -1; i--) { L(p_IP, i, flag, k[i]); } } int[] c = new int[64]; for (int i = 0; i < IP_1.length; i++) { c[i] = p_IP[IP_1[i] - 1]; } byte[] c_byte = new byte[8]; for (int i = 0; i < 8; i++) { c_byte[i] = (byte) ((c[8 * i] << 7) + (c[8 * i + 1] << 6) + (c[8 * i + 2] << 5) + (c[8 * i + 3] << 4) + (c[8 * i + 4] << 3) + (c[8 * i + 5] << 2) + (c[8 * i + 6] << 1) + (c[8 * i + 7])); } return c_byte; } public void L(int[] M, int times, int flag, int[] keyarray) { int[] L0 = new int[32]; int[] R0 = new int[32]; int[] L1 = new int[32]; int[] R1 = new int[32]; int[] f = new int[32]; System.arraycopy(M, 0, L0, 0, 32); System.arraycopy(M, 32, R0, 0, 32); L1 = R0; f = fFuction(R0, keyarray); for (int j = 0; j < 32; j++) { R1[j] = L0[j] ^ f[j]; if (((flag == 0) && (times == 0)) || ((flag == 1) && (times == 15))) { M[j] = R1[j]; M[j + 32] = L1[j]; } else { M[j] = L1[j]; M[j + 32] = R1[j]; } } } public int[] fFuction(int[] r_content, int[] key) { int[] result = new int[32]; int[] e_k = new int[48]; for (int i = 0; i < E.length; i++) { e_k[i] = r_content[E[i] - 1] ^ key[i]; } /********S Box replacement: change from 48 bit to 32-bit, now divide e ﹐ UK, and then replace*********/ int[][] s = new int[8][6]; int[] s_after = new int[32]; for (int i = 0; i < 8; i++) { System.arraycopy(e_k, i * 6, s[i], 0, 6); int r = (s[i][0] << 1) + s[i][5];//Abscissa int c = (s[i][1] << 3) + (s[i][2] << 2) + (s[i][3] << 1) + s[i][4];//Ordinate String str = Integer.toBinaryString(S_Box[i][r][c]); while (str.length() < 4) { str = "0" + str; } for (int j = 0; j < 4; j++) { int p = Integer.valueOf(str.charAt(j)); if (p == 48) { p = 0; } else if (p == 49) { p = 1; } else { System.out.println("To bit error!"); } s_after[4 * i + j] = p; } } /******S End of box replacement*******/ /****P Box substitution * * **/ for (int i = 0; i < P.length; i++) { result[i] = s_after[P[i] - 1]; } return result; } /** * Generate subkey **/ public void generateKeys(String key) { while (key.length() < 8) { key = key + key; } key = key.substring(0, 8); byte[] keys = key.getBytes(); int[] k_bit = new int[64]; //Fetching value for (int i = 0; i < 8; i++) { String k_str = Integer.toBinaryString(keys[i] & 0xff); if (k_str.length() < 8) { int k_size = k_str.length(); for (int t = 0; t < 8 - k_size; t++) { k_str = "0" + k_str; } } for (int j = 0; j < 8; j++) { int p = Integer.valueOf(k_str.charAt(j)); if (p == 48) { p = 0; } else if (p == 49) { p = 1; } else { System.out.println("To bit error!"); } k_bit[i * 8 + j] = p; } } //K? Bit is the initial 64 bit long key, and the next step is to replace it /***********PC-1 Compression****************/ int[] k_new_bit = new int[56]; for (int i = 0; i < PC1.length; i++) { k_new_bit[i] = k_bit[PC1[i] - 1];/////Note for this minus 1 } /**************************/ int[] c0 = new int[28]; int[] d0 = new int[28]; System.arraycopy(k_new_bit, 0, c0, 0, 28); System.arraycopy(k_new_bit, 28, d0, 0, 28); for (int i = 0; i < 16; i++) { int[] c1 = new int[28]; int[] d1 = new int[28]; if (LFT[i] == 1) { System.arraycopy(c0, 1, c1, 0, 27); c1[27] = c0[0]; System.arraycopy(d0, 1, d1, 0, 27); d1[27] = d0[0]; } else if (LFT[i] == 2) { System.arraycopy(c0, 2, c1, 0, 26); c1[26] = c0[0]; c1[27] = c0[1];//It was written as c1 before the hand was broken System.arraycopy(d0, 2, d1, 0, 26); d1[26] = d0[0]; d1[27] = d0[1]; } else { System.out.println("LFT Error!"); } int[] tmp = new int[56]; System.arraycopy(c1, 0, tmp, 0, 28); System.arraycopy(d1, 0, tmp, 28, 28); for (int j = 0; j < PC2.length; j++) {//PC2 compression replacement sub_key[i][j] = tmp[PC2[j] - 1]; } c0 = c1; d0 = d1; } } }
CustomDESTest
package com.lcx.des; public class CustomDESTest { public static void main(String[] args){ String origin="https://www.lisongbai.top"; System.out.println("Original text:\n"+origin); CustomDES customDES=new CustomDES("LCX",origin); byte[] c=customDES.deal(origin.getBytes(),1); System.out.println("Ciphertext:\n"+new String(c)); byte[]p=customDES.deal(c,0); byte[] p_d=new byte[origin.getBytes().length]; System.arraycopy(p,0,p_d,0,origin.getBytes().length); System.out.println("Plaintext:\n"+new String(p)); } }
The test results are as follows:
Feel the experience
Through the implementation of DES encryption and decryption algorithm by myself, I have a deeper understanding of the process of DES encryption and decryption. I had a general understanding of the process in the classroom before, but I didn't know much about many details. In this big assignment, I looked up a lot of materials and had more experience of DES encryption algorithm.
DES encryption is a classical algorithm of stacking encryption. Through its implementation process, it is found that it uses many permutation methods, and uses the combination of chaos and diffusion. Each combination replaces first and then displaces, and has 16 rounds in total. Among them, the asymmetric operation of S-box is fully utilized, which greatly increases the difficulty of cracking. In the absence of a key, the evil of the cracker can be broken through exhaustive method Decryption key, this method is time-consuming and laborious, so the security of DES is very high.
Through this big assignment, I realized the interesting part of encryption design in cryptography. When I only touched the theoretical knowledge, I felt that the encryption algorithm was just a boring iterative operation, and only after practice did I feel that the boring iterative operation was the secret of its design. In the later learning process, we should try our best to know what it is and why it is.
To read more blogs, please click here to view – > https://lisongbai.top/


