Blog has also been open for a long time, has not been to write a blog, the main reason is that I am lazy ~~~This blog is a good start for 2017, but also to 2016 draw a period, without regret.

Let's formally enter today's theme: Bessel Curve.

First, let's see what a Bessel curve is.

B ezier curve, also known as Baez Curves or Bezier curves are mathematical curves applied to two-dimensional graphics applications. The Bessel Curve was widely published in 1962 by Pierre B zier, a French engineer, who used the Bessel Curve to design the main body of a car. Bessel curve was originally developed by Paul de Casteljau in 1959 using the de Casteljau algorithm to obtain the Bessel curve by stable numerical method.

Now that we understand what Bessel curves are, let's look at the classification of Bessel curves. Before we talk about classification, we should first mention two concepts: data point and control point.

Data Points: The starting and ending points of a curve.

Control Point: As the name implies, it is the point that controls the degree of curve bending.

The curves are classified as follows:

First order curve:

Formula: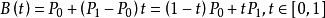

Dynamic charts: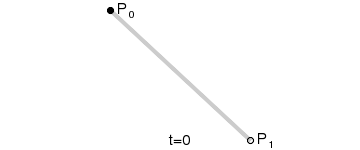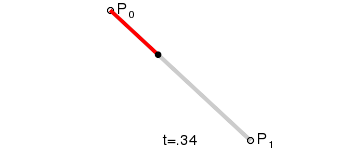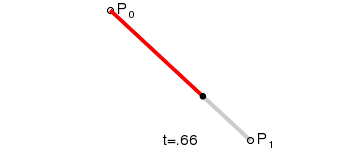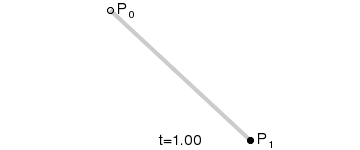

Principle: A straight line composed of continuous points from P 0 (starting point) to P 1 (ending point). The first order curve has no control points.

Second order curve:

Formula: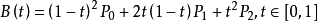

Static diagram: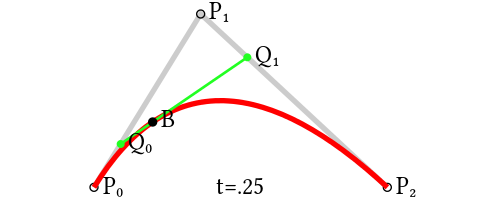

Dynamic charts: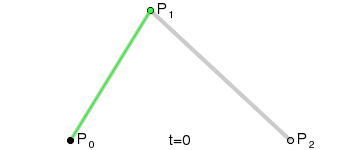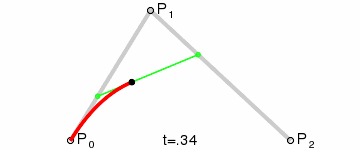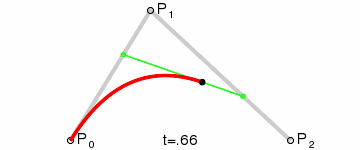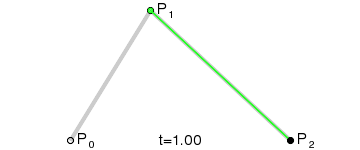

Principle: Point Q0(t) changes from P0 to P1, describing a linear B zier curve.

Point Q1(t) changes from P1 to P2, describing a linear B zier curve.

The change of point B (t) from Q0(t) to Q1(t) describes a quadratic B zier curve.

P0 is the starting point, P2 is the end point, and P1 is the control point.

Third-order curve:

Formula: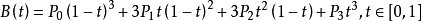　

Static diagram: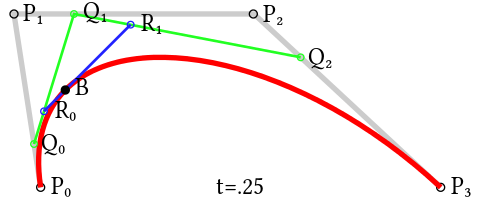　　

Dynamic charts: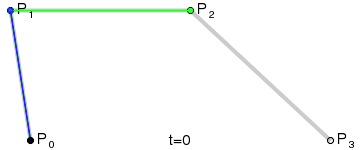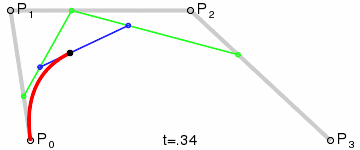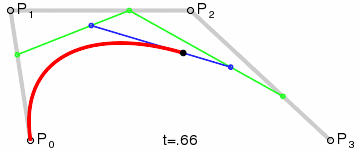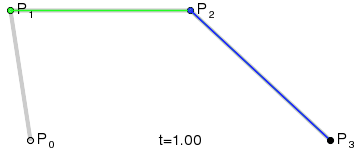

Principle: Its principle is similar to that of second-order curve, mainly with more control points.

In addition to the above three kinds of Bessel curve classification, of course, there are fourth-order curve, fifth-order curve...

Having said so much, how on earth should we use the Bessel curve? Is there any way to provide us with it?

Of course, when we customize View, we use a class called Path, in which there are two methods: quadTo (drawing second-order curve) and cubicTo (drawing third-order curve). These two methods I will simply use two pieces of code to illustrate. Here I will post the main code:

The main code block of the second order curve:

@Override
    protected void onDraw(Canvas canvas) {
        //Draw a straight line
        mPaint.setColor(Color.BLACK);
        mPaint.setStrokeWidth(4);
        canvas.drawLine(firstPoint.x,firstPoint.y,midPoint.x,midPoint.y,mPaint);
        canvas.drawLine(lastPoint.x,lastPoint.y,midPoint.x,midPoint.y,mPaint);
       //Draw points
        mPaint.setStrokeWidth(20);
        canvas.drawPoint(firstPoint.x,firstPoint.y,mPaint);
        canvas.drawPoint(lastPoint.x,lastPoint.y,mPaint);
        canvas.drawPoint(midPoint.x,midPoint.y,mPaint);
       //Draw second-order curves
        mPaint.setColor(Color.BLUE);
        mPaint.setStrokeWidth(8);
        Path path = new Path();
        path.moveTo(firstPoint.x,firstPoint.y);
        path.quadTo(midPoint.x,midPoint.y,lastPoint.x,lastPoint.y);
        canvas.drawPath(path,mPaint);
    }

Design sketch: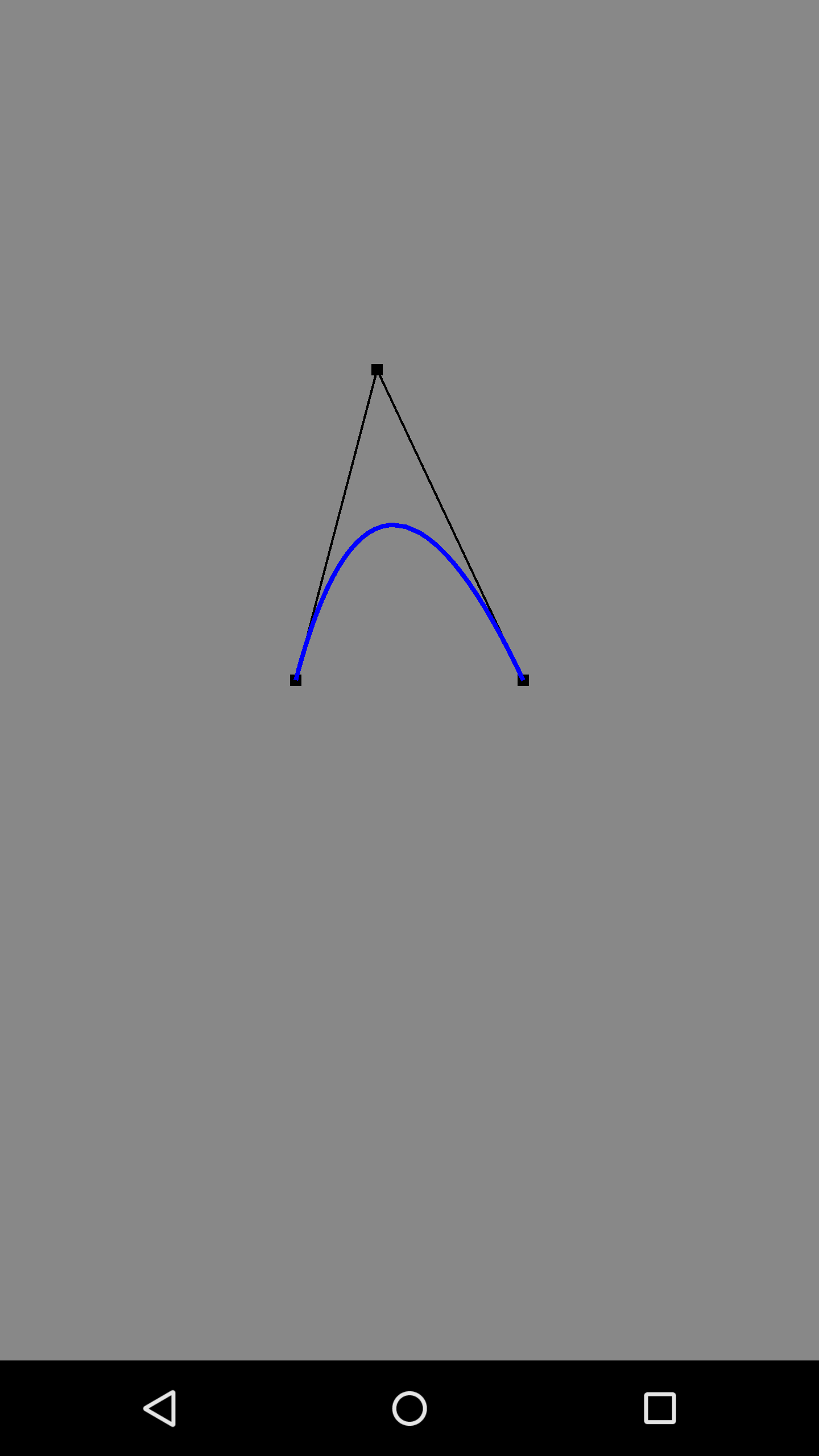(ps: No dynamic graphics on mobile phones)

The main code block of third-order curve:

@Override
    protected void onDraw(Canvas canvas) {
       mPaint.setColor(Color.BLACK);
        //Draw a straight line
        mPaint.setStrokeWidth(4);
        canvas.drawLine(firstPoint.x,firstPoint.y,control1.x,control1.y,mPaint);
        canvas.drawLine(midPoint1.x,midPoint1.y,midPoint2.x,midPoint2.y,mPaint);
        canvas.drawLine(midPoint2.x,midPoint2.y,lastPoint.x,lastPoint.y,mPaint);
        //Draw points
        mPaint.setStrokeWidth(20);
        canvas.drawPoint(firstPoint.x,firstPoint.y,mPaint);
        canvas.drawPoint(lastPoint.x,lastPoint.y,mPaint);
        canvas.drawPoint(midPoint1.x,midPoint1.y,mPaint);
        canvas.drawPoint(midPoint2.x,midPoint2.y,mPaint);
        //Draw a third-order curve
        mPaint.setColor(Color.BLUE);
        mPaint.setStrokeWidth(8);
        Path path = new Path();
        path.moveTo(firstPoint.x,firstPoint.y);
        path.cubicTo(midPoint1.x,midPoint1.y,midPoint2.x,midPoint2.y,
        lastPoint.x,lastPoint.y);
        canvas.drawPath(path,mPaint);
    }

Design sketch: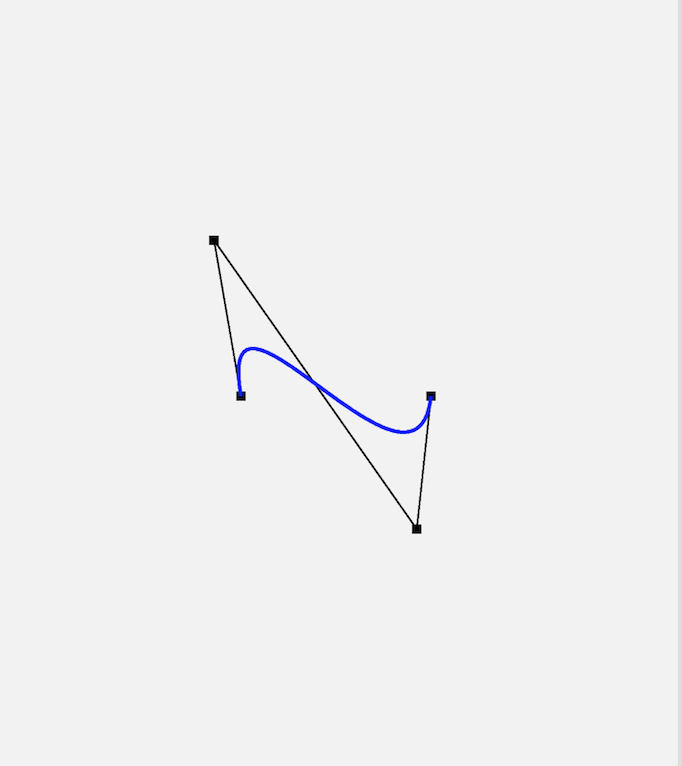(ps: Still won't do dynamic graphics on mobile phones)　　

Well, at this point, the analysis of Bessel curve has been finished. If you want to know more about Bessel curve, you can see this website:

https://en.wikipedia.org/wiki/B%C3%A9zier_curve

Because of the first blog, some places are not very well expressed, please forgive me. If there are good suggestions and shortcomings, we hope to point out that we should change them modestly.