Preorder traversal and inorder traversal restore binary tree
Link: pre order + mid order restore binary tree
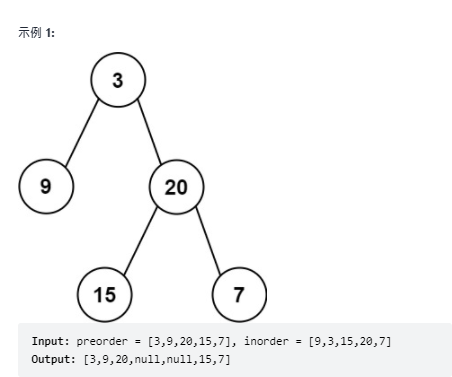
Idea:
- Determine the root node of the binary tree in the preorder traversal result (reason: the preorder traversal first traverses the root node, traverses the left subtree of the root, and then traverses the right subtree of the root);
- Find the position pos of the root in the middle order traversal result. Take pos as the dividing point. The left is the position of the left subtree element of the root, and the right is the position of the right subtree element of the root;
- Restore the root node;
- Recursively restore the left subtree of the root;
- Recursive reduction of right subtree of root
Code implementation:
class Solution {
int index=0; //Used to mark the position of the root in the preorder traversal
TreeNode rebuilderTree(int[] preorder,int[] inorder,int left, int right){
if(index>=preorder.length || left >= right){
return null;
}
//Determine the position elements of the left and right subtrees of the root from the middle order traversal results
int pos=left;
while(pos<right){
if(inorder[pos]==preorder[index]){
//Indicates that the root node was found
break;
}
pos++;
}
// Determine the root from the preorder traversal result, that is, the position of the index. preorder[index] is the position of the root
//Restore root node of binary tree
TreeNode root=new TreeNode(preorder[index]);
index++;
//Recursively restore the left subtree of the root
root.left=rebuilderTree(preorder,inorder,left,pos);
//Recursive reduction of right subtree of root
root.right=rebuilderTree(preorder,inorder,pos+1,right);
return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
index=0;
return rebuilderTree(preorder, inorder,0,inorder.length);
}
}
Middle order traversal and post order traversal restore binary tree
Link: middle order + post order restore binary tree
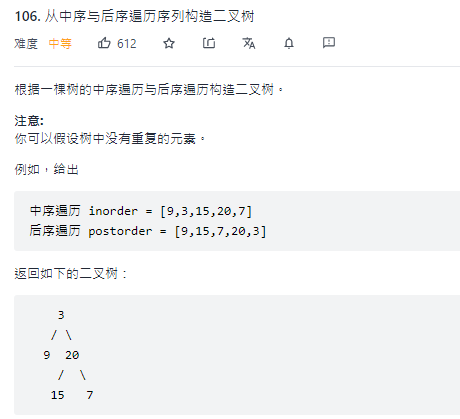
Idea:
- Determine the root node of the binary tree in the post order traversal result (reason: the post order traversal first traverses the left subtree of the root, then the right subtree of the root, and finally the root node);
- Find the position pos of the root in the middle order traversal result. Take pos as the dividing point. The left is the position of the left subtree element of the root, and the right is the position of the right subtree element of the root;
- Restore the root node;
- Recursively restore the right subtree of the root;
- Recursively restore the left subtree of the root
Code implementation:
class Solution {
int index=0; //Used to mark the position of the root in the preorder traversal
TreeNode rebuilderTree(int[] postorder,int[] inorder,int left, int right){
if(index<0 || left >= right){
return null;
}
//Determine the position elements of the left and right subtrees of the root from the middle order traversal results
int pos=left;
while(pos<right){
if(inorder[pos]==postorder[index]){
//Indicates that the root node was found
break;
}
pos++;
}
// Determine the root from the preorder traversal results, that is, the position of the index. The postorder[index] is the position of the root
//Restore root node of binary tree
TreeNode root=new TreeNode(postorder[index]);
index--;
//Recursive reduction of right subtree of root
root.right=rebuilderTree(postorder,inorder, pos+1,right);
//Recursively restore the left subtree of the root
root.left=rebuilderTree(postorder,inorder,left ,pos);
return root;
}
public TreeNode buildTree(int[] inorder, int[] postorder) {
index=postorder.length-1;
return rebuilderTree(postorder, inorder,0,inorder.length);
}
}
Binary tree construction string
Links: binary tree construction strings
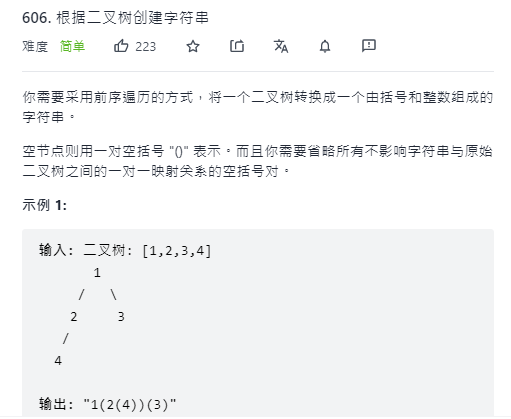
Idea:
This topic uses string. Because string is an immutable type and needs to be spliced, we use stringbuilder;
Note: the left parenthesis in the title cannot be omitted, otherwise the position of the left and right subtrees cannot be distinguished;
Code implementation:
class Solution {
public void preorder(TreeNode root, StringBuilder str) {
//The tree is empty
if (root == null) {
return;
}
//Convert root node (i.e. print)
str.append(root.val);
//Left subtree of recursive transformation root
//There are two situations
if (root.left != null) {
str.append('(');
preorder(root.left, str);
str.append(')');
}
if (root.left == null && root.right != null) {
str.append('(');
str.append(')');
}
//Right subtree of recursive transformation root
if (root.right != null) {
str.append('(');
preorder(root.right, str);
str.append(')');
}
}
public String tree2str(TreeNode root) {
StringBuilder str = new StringBuilder();
preorder(root, str);
return str.toString();
}
}
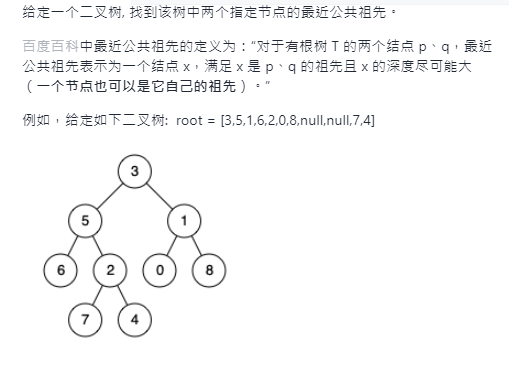
Find the nearest common ancestor of binary tree
Idea:
It can be analyzed and discussed in three situations:
Case 1: the binary tree adopts parent representation or child parent representation;
Seeking the common ancestor becomes the problem of finding the intersection point of two linked lists;
Case 2:
If the binary tree is a binary search tree, the so-called binary search tree satisfies: (1) the left subtree node whose root node is greater than the root; (2) The root node is smaller than the right subtree node of the root;
There are four ways to seek common ancestors:
Suppose a given two nodes, one is x and the other is y;
(1) When x == root or y ==root, the nearest common ancestor must be the root node; (reason: the root node is the ancestor of all nodes)
(2) When x. Data < root.data & & Y.Data > root.data, or when x. Data > root.data & & Y.Data < root.data, the nearest common ancestor is also the root node (reason: X and y are on both sides of the root node);
(3) When x. Data < root. Data & & Y.Data < root. Data, X and y are both in the left subtree of the root, so the nearest common ancestor can be found directly in the left subtree of the root;
(4) When x. Data > root.data & & Y.Data > root.data, both X and y are in the right subtree of the root, so the nearest common ancestor can be found directly in the right subtree of the root;
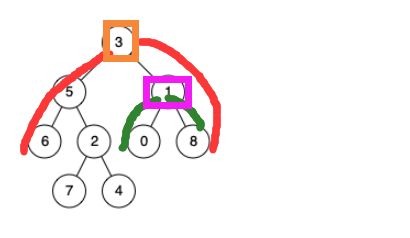
Case 3: the binary tree is an ordinary binary tree;
Then:
- Inspired by case 1, just find those nodes in the path from the root node to a node and save them; Because when the node in the path is found, it needs to be compared from bottom to top, so it is saved with the help of stack;
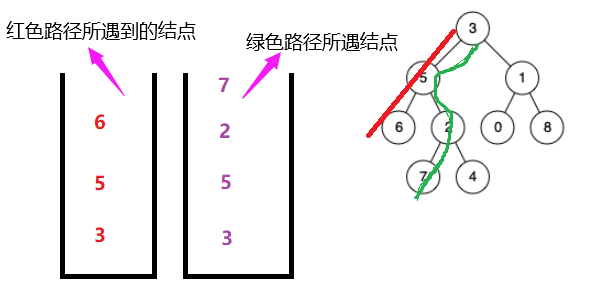
In this case
(1) When the elements stored in the stack are not equal, let more elements out of the stack;
(2) When the value range is the same and different, the stack is displayed at the same time;
(3) Common ancestor is the element with the same number of elements in the stack and the same value range;
Code implementation:
class Solution {
//Get all the nodes in the path from the root node to a node
boolean getPathNode(TreeNode root,Stack<TreeNode> sPath,TreeNode node ){
if(node ==null || root==null){
//The tree is empty or the node is empty
return false;
}
sPath.push(root);
if(root==node){
//Indicates the same node
return true;
}
//Find in the left subtree
if(getPathNode(root.left,sPath,node)){
return true;
}
//Find in right subtree
if(getPathNode(root.right,sPath,node)){
return true;
}
sPath.pop();
return false;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//Detect given parameters
if(root==null ||p==null ||q==null){
return null;
}
//Find all nodes contained in the corresponding path from root to p,q
//Save to stack
Stack<TreeNode> pPath=new Stack();
Stack<TreeNode> qPath=new Stack();
getPathNode(root,pPath,p);
getPathNode(root,qPath,q);
int pSize=pPath.size();
int qSize=qPath.size();
while(!pPath.empty() && !qPath.empty()){
if(pPath.peek()==qPath.peek()){
return pPath.peek();
}
if(pSize>qSize){
//Let more out of the stack
pPath.pop();
pSize--;
}else if(pSize<qSize){
qPath.pop();
qSize--;
}else{
//When two are the same, they come out of the stack at the same time
pPath.pop();
qPath.pop();
pSize--;
qSize--;
}
}
return null;
}
}
- Similarly, inspired by situation 2:
- If we know the position of a node in its subtree, we can also find the common ancestor;
The code is as follows:
class Solution {
boolean isNodeInTree(TreeNode root,TreeNode node){
//Check whether the node is in the tree
if(root==null || node ==null){
return false;
}
if(root==node){
return true;
}
if(isNodeInTree(root.left,node)){
return true;
}
return isNodeInTree(root.right,node);
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//Empty tree
if(root==null){
return null;
}
//Tree is not empty
//p and q have a position at the root, and the common ancestor is the root
if(p == root|| q == root){
return root;
}
boolean ispInLeft=false;
boolean ispInRight=false;
boolean isqInLeft=false;
boolean isqInRight=false;
//Check whether p is in the left subtree of root
if(isNodeInTree(root.left,p)){
ispInLeft=true;
ispInRight=false;
}else{
ispInLeft=false;
ispInRight=true;
}
//Check whether q is in the left subtree of root
if(isNodeInTree(root.left,q)){
isqInLeft=true;
isqInRight=false;
}else{
isqInLeft=false;
isqInRight=true;
}
//Check whether both p and q are in the left subtree of root
if(ispInLeft && isqInLeft){
return lowestCommonAncestor(root.left,p,q);
}else if(ispInRight && isqInRight){
return lowestCommonAncestor(root.right,p,q);
}else{
return root;
}
}
}