C language daily practice
November 3, 2021
Title Description
An even number can always be expressed as the sum of two prime numbers
analysis
I'm curious about what this question asks me to do, proof? I can only think of this, so simply prove it (for fun) (but most people on the Internet regard it as "entering an even number and returning two prime addends".
In his 1742 letter to Euler, Goldbach put forward the following conjecture: any integer greater than 2 can be written as the sum of three prime numbers. But Goldbach couldn't prove it himself, so he wrote to ask the famous great mathematician Euler to help prove it, but Euler couldn't prove it until he died.
In 1966, Chen Jingrun proved that "1 + 2" was established, that is, "any sufficiently large even number can be expressed as the sum of two prime numbers, or the sum of a prime number and a semi prime number
The common conjecture statement today is Euler's version, that is, any even number greater than 2 can be written as the sum of two prime numbers, also known as "strong Goldbach conjecture" or "Goldbach conjecture about even numbers".
——Baidu Encyclopedia
Although I can't prove this conjecture in C language, I can set a range and prove that the numbers in the range meet this condition.
Idea:
Three layer loop: the first layer traverses all even numbers greater than 2 (given range), the second layer traverses the first prime addend, and the third layer traverses the second prime addend. Only when all even numbers have two prime addends (addends of prime numbers) can it be proved that within the range of the number, an even number can always be expressed as the sum of two prime numbers.
code implementation
When the number range exceeds 100000, the program runs very slowly and prints one line in half a day.
//Goldbach conjecture - any even number greater than 2 is the sum of two prime numbers
#include <stdio.h>
//0-18446744073709551615 (0 to 2^64 - 1) unsigned long long
//0-4294967295 (0 to 2^32 - 1) unsigned long
typedef unsigned long long MY_TYPE; //Redefine a data type as MY_TYPE
MY_TYPE MAX_RANGE = 10000; //My compilation environment runs very slowly over 10000, and hardly moves over 100000
/*
* Judge whether it is a prime number. If yes, it returns 1, and if no, it returns 0
* */
int is_Prime(MY_TYPE num)
{
MY_TYPE i = 0;
for(i = 2; i < num; i++) //num can be optimized to sqrt(num)
{
/* If the number has a positive factor other than 1, it is not a prime number */
if(num % i == 0)
return 0;
}
return 1;
}
int main()
{
MY_TYPE x = 0, y = 0, z = 0;
for(z = 4; z <= MAX_RANGE; z++) //0 and 2 do not participate in judgment
{
if(z % 2 == 0) //If z is even
{
for(x = 2; x <= MAX_RANGE; x++) //The minimum prime number is 2
{
if(is_Prime(x)) //If x is prime
{
for(y = 2; y <= MAX_RANGE; y++) //The minimum prime number is 2
{
if(is_Prime(y)) //If y is prime
{
if(z == x + y) //The even number z is the sum of two prime numbers
goto LOOP_OK; //Just jump out of these two layers of circulation
}
}
}
}
if(x == MAX_RANGE && y == MAX_RANGE)
printf("%llu Not equal to the sum of two primes", z); //Proof failed!
LOOP_OK:
printf("%llu = %llu + %lu\n", z, x, y); //Print z=x+y
}
}
/* Prove successful (4-MAX_RANGE)!*/
printf("4 to %llu Even numbers in can be expressed as the sum of two prime numbers", MAX_RANGE);
return 0;
}
Operation results
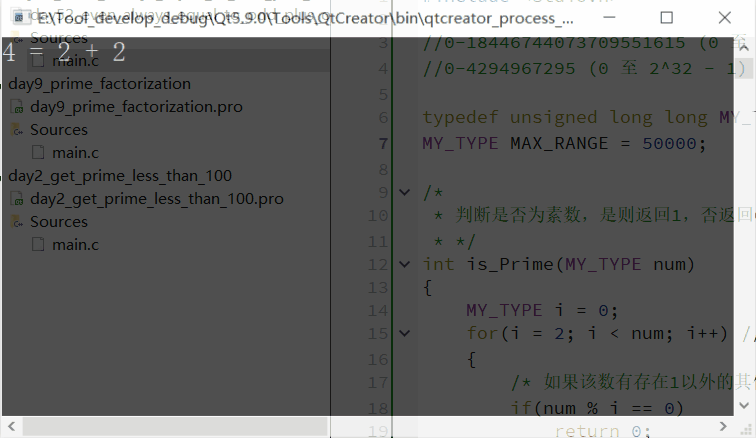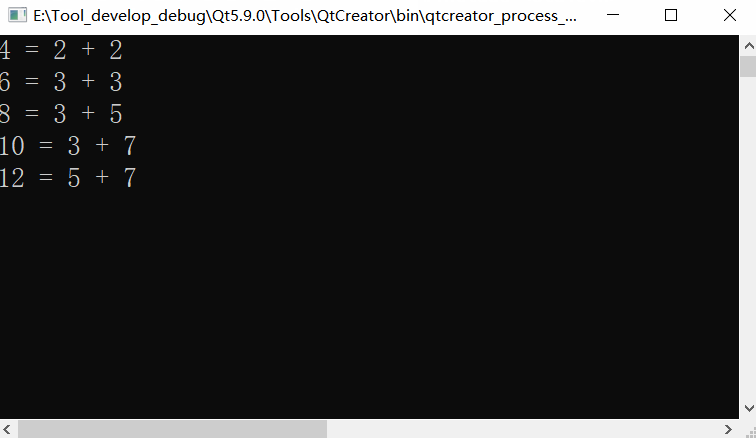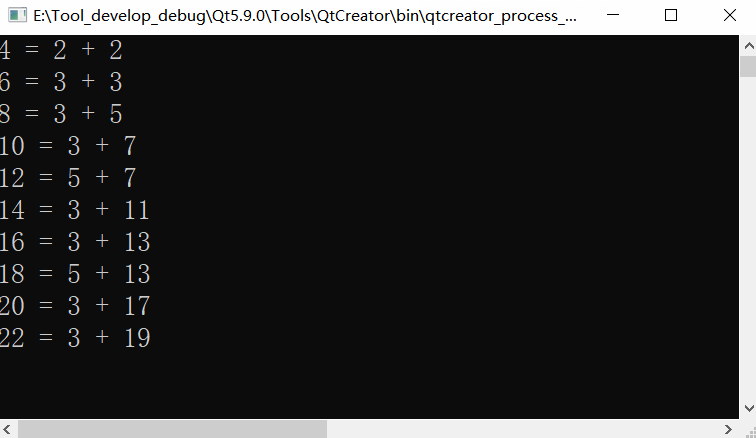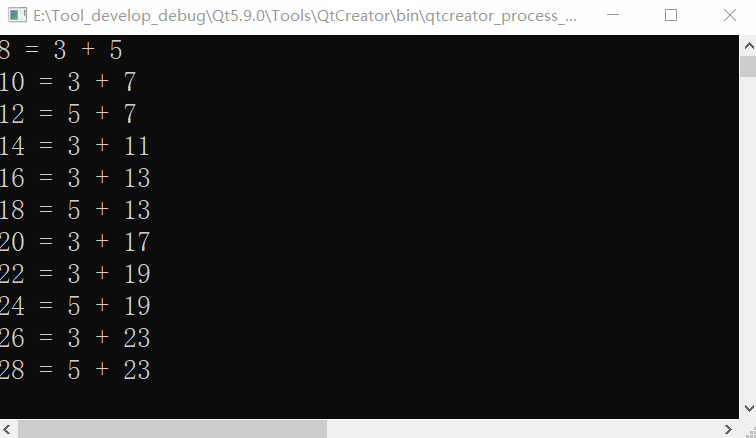
The number range is 4-2000, which doesn't look slow
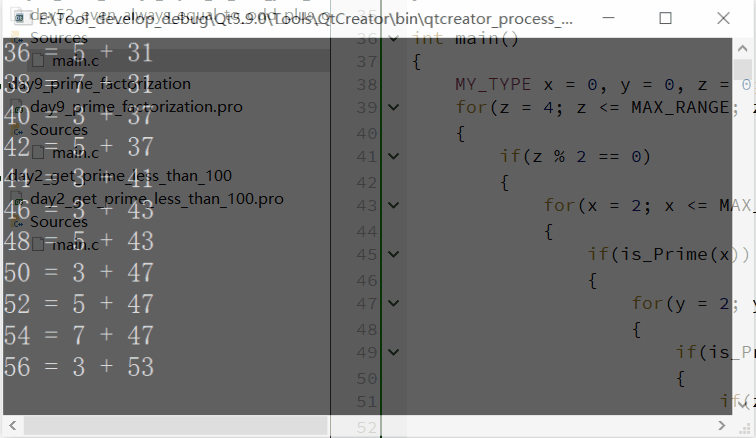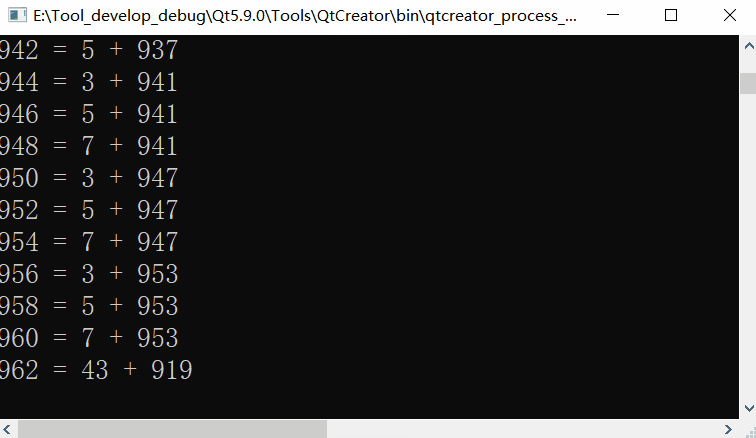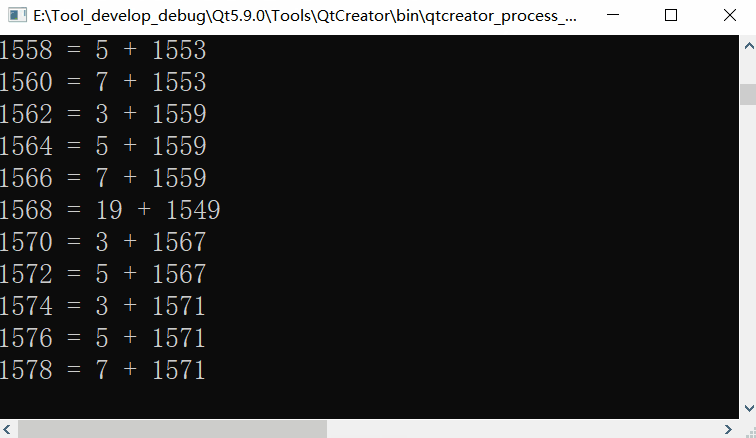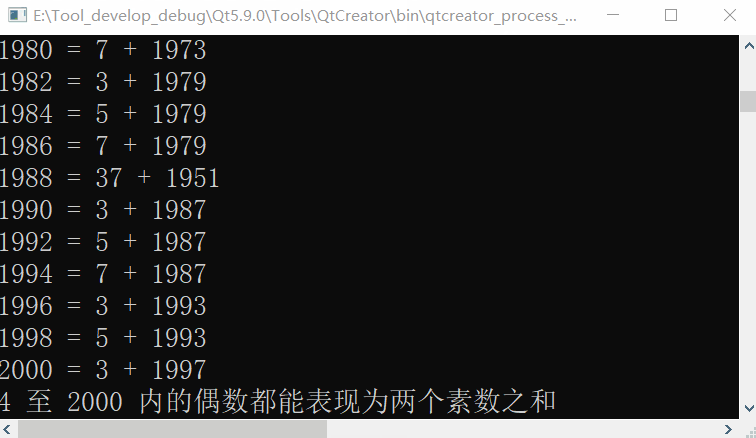
Adjusting the digital range to 4-10000 obviously slows down, but the actual effect is faster than this (there is a delay in the screen recording software)
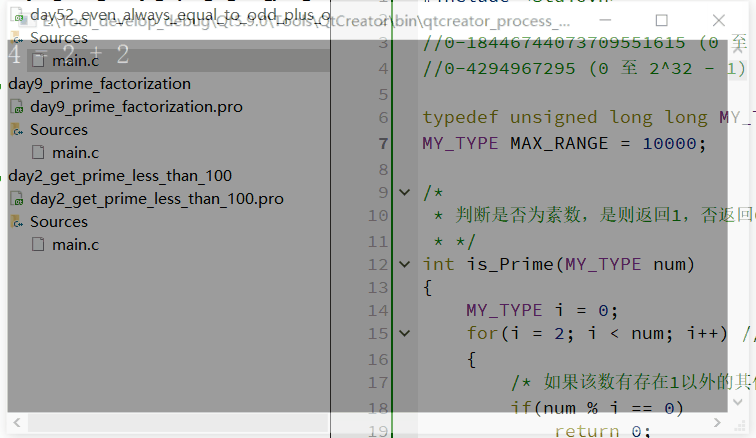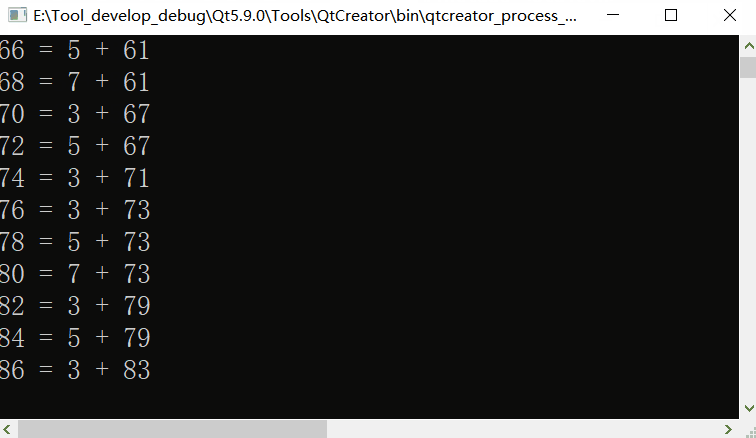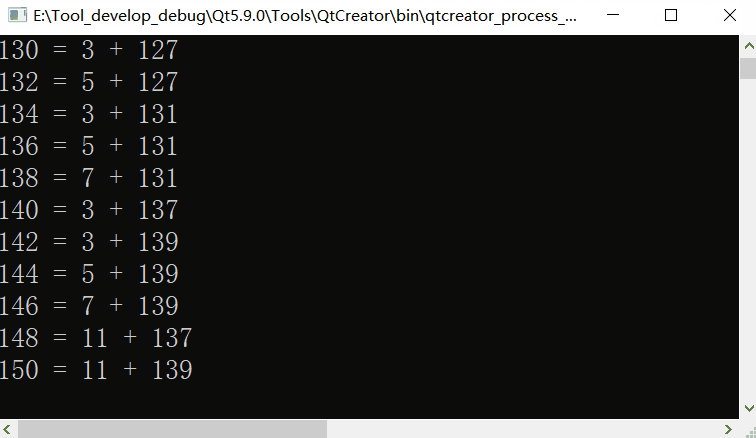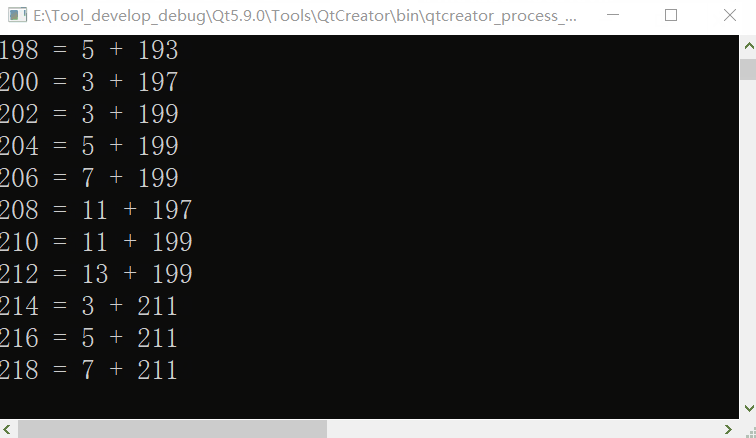
Adjust the number range to 4-50000, and the speed has caught up with the tortoise. Let alone increase it.
Later improvement
The efficiency of the previous version was too low. When the digital range was adjusted to 100000, the program was stuck and had to be optimized:
Of course, my algorithm is very poor. If you have a better method, you can also share it.
Changes in this optimization
- The prime judgment range is reduced to num ½ , Reduce the number of runs by more than half
- Without even number judgment, directly + 2, and the number of runs is reduced by half
- The second prime addend reverse polling, the key optimization, greatly reduces the number of runs
`
Setting the range directly at 4-264 can run smoothly, but I don't have the patience to wait for it to run...
The range of numbers should be increased, but I don't know what method to use at present (I'm not interested!)
//Goldbach conjecture - any even number greater than 2 is the sum of two prime numbers
#include <stdio.h>
#include <math.h>
//0-18446744073709551615 (0 to 2^64 - 1) unsigned long long
//0-4294967295 (0 to 2^32 - 1) unsigned long
typedef unsigned long long MY_TYPE; //Redefine a data type as MY_TYPE
MY_TYPE MAX_RANGE = 18446744073709551615; //Big BOOS
/*
* Judge whether it is a prime number. If yes, it returns 1, and if no, it returns 0
* */
int is_Prime(MY_TYPE num)
{
MY_TYPE i = 0;
if(num < 2)
return 0;
for(i = 2; i <= sqrt(num); i++) //#####Optimize 1 and reduce the number of runs by more than twice#####
{
/* If the number has a positive factor other than 1, it is not a prime number */
if(num % i == 0)
return 0;
}
return 1;
}
int main()
{
MY_TYPE x = 0, y = 0, z = 0;
for(z = 4; z <= MAX_RANGE; z += 2) //#####Optimize 2, directly + 2, and reduce the number of runs by half#####
{
for(x = 2; x <= MAX_RANGE; x++) //The minimum prime number is 2
{
if(is_Prime(x)) //If x is prime
{
for(y = z; y >= 2; y--) //#####Optimization 3, greatly reducing the number of runs######
{
if(is_Prime(y)) //If y is prime
{
if(z == x + y) //The even number z is the sum of two prime numbers
goto LOOP_OK; //Just jump out of these two layers of circulation
}
}
}
}
if(x == MAX_RANGE && y == 2)
printf("%llu Not equal to the sum of two primes", z); //Proof failed!
LOOP_OK:
printf("%llu = %llu + %lu\n", z, x, y); //Print z=x+y
}
/* Prove successful (4-MAX_RANGE)!*/
printf("4 to %llu Even numbers in can be expressed as the sum of two prime numbers", MAX_RANGE);
return 0;
}
Operation effect when the maximum digital range is set to 10000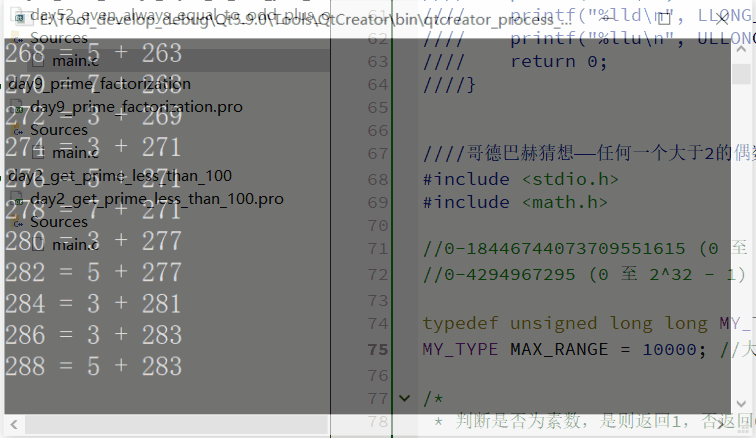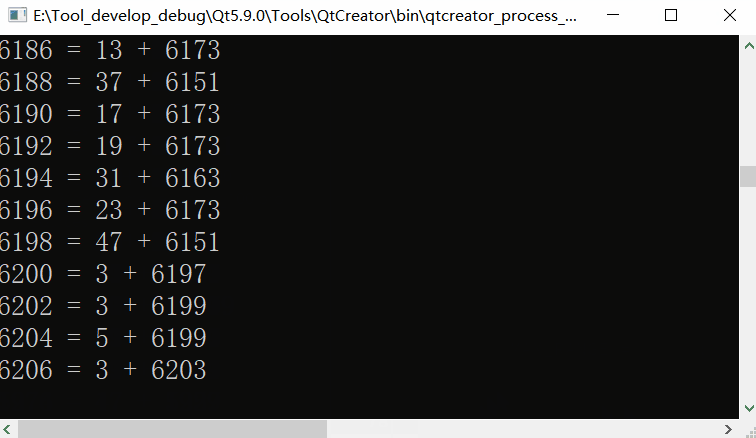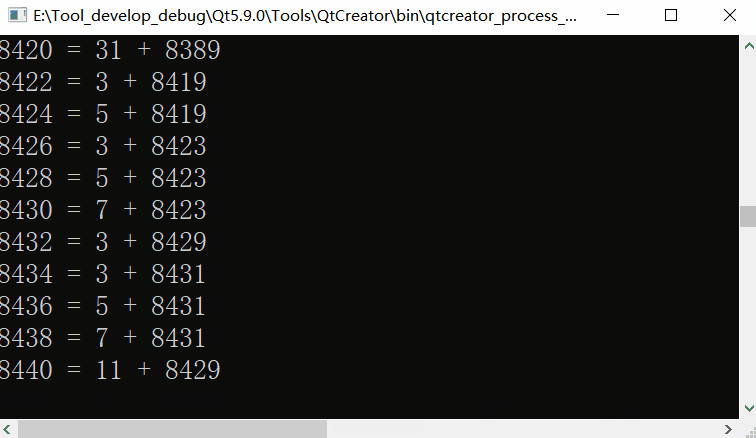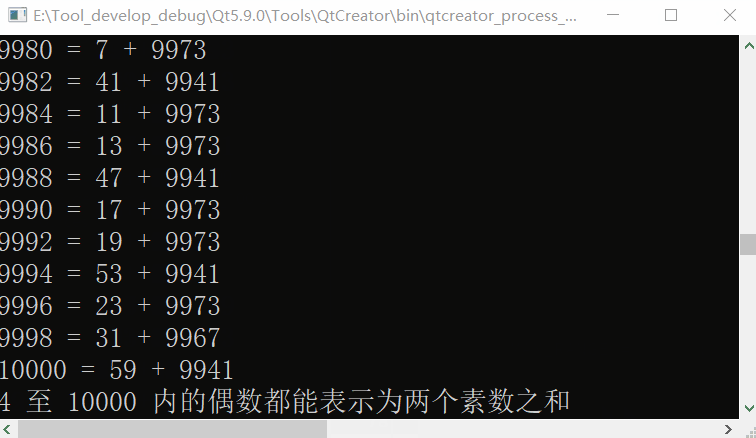
When the maximum digital range was set to 18446744073709551615 (264), the speed hardly changed. Now I finally know why the algorithm is important.

Online reference
There is basically no proof of conjecture on the Internet (specify the number range). There may be, but it is too tired to find the information on the Internet, which is time-consuming and laborious.
Original link: https://www.runoob.com/cprogramming/c-exercise-example84.html
What a coincidence, he said so, but there seems to be a problem with his program - now the minimum prime is not 1, so I posted a note (user comment) under the website.

However, there are still problems with this Code:
#include<stdio.h>
#include<math.h>
int IsPrime(int n)
{
int i;
if(n == 1)
return 0;
for(i = 2; i <= sqrt(n); i++)
if(n%i == 0)
return 0;
return 1;
}
void divide_even(int even,int *a,int *b)
{
int i;
for(i = 2; i < even; i++)
{
if(IsPrime(i)&&IsPrime(even - i))
break;
}
*a = i;
*b = even - i;
}
int main(void)
{
int n,a,b;
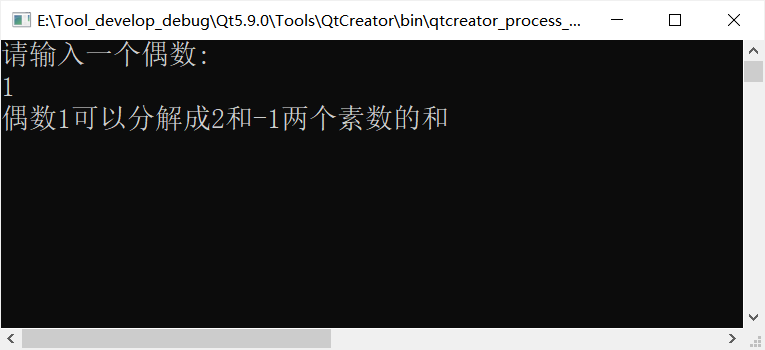
printf("Please enter an even number:\n");
scanf("%d",&n);
divide_even(n,&a,&b);
printf("even numbers%d Can be decomposed into%d and%d Sum of two prime numbers",n,a,b);
}
Error 1:0 is not prime
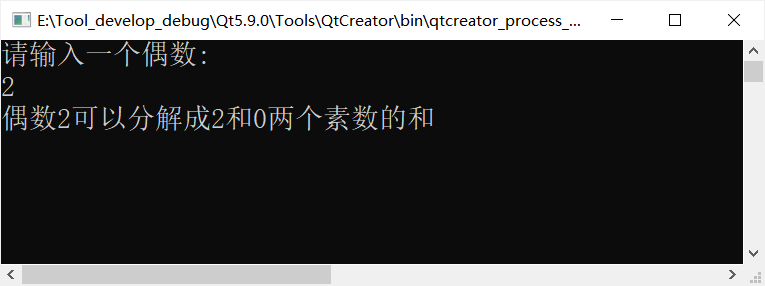
Error 2: the smallest prime is 2, so negative numbers are not prime, 😁 I feel a little too much.
Error 3: I don't know if this is a mistake, or it may be my mistake....