All source shortest path
Like Floyd, Johnson is an algorithm that can find the shortest path between any two points on a nonnegative ring graph.
1. Algorithm overview
The shortest path between any two points can be solved by enumerating the starting points and running Bellman Ford algorithm n times. The time complexity is O(\(n^2 m \). It can also be solved directly by Floyd algorithm. The time complexity is O(\(n^3 \))
The time complexity of the Dijkstra algorithm for heap optimization to find the shortest path of a single source is better than Bellman Ford. If you enumerate the starting points and run the Dijkstra algorithm n times, it can be in O(\(n m\log m \))
However, Dijkstra algorithm can not correctly solve the shortest path with negative weight edges, so we need to preprocess the edges on the original graph to ensure that the edge weights of all edges are non negative.
An easy way to think of is to add a positive number x to the edge weights of all edges at the same time, so that the edge weights of all edges are non negative. If the shortest path from the start point to the end point on the new graph passes through k edges, the actual shortest path can be obtained by subtracting \ (k\times x \) from the shortest path.
But this approach is wrong. Consider the following figure:
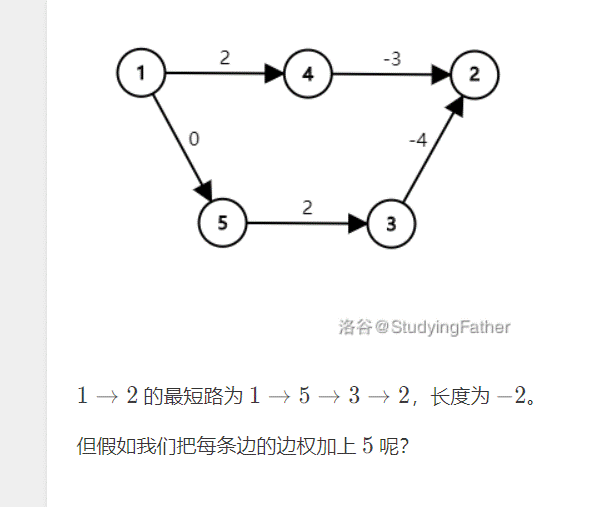
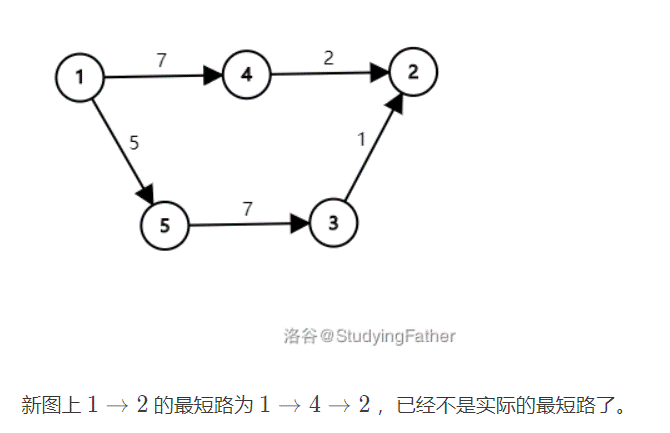
Johnson algorithm uses another method to re label the edge weight for each edge.
We create a new virtual node (here we set its number to 0). Connect an edge with edge weight 0 from this point to all other points.
Next, the bellman Ford algorithm is used to find the shortest path from point 0 to all other points, which is recorded as \ (h_i \)
If there is an edge whose edge weight is w from point u to point v, we reset the edge weight of the edge to \ (W + h_-h_v \).
Next, taking each point as the starting point, the Dijkstra algorithm of running n rounds can find the shortest path between any two points.
It is easy to see that the time complexity of the algorithm is O(\(n m\log m \))
2. Proof of correctness
Why is it correct to re label edge weights in this way?
Before discussing this problem, let's discuss a physical concept - potential energy.
Potential energy such as gravitational potential energy and electric potential energy have a characteristic. The change of potential energy is only related to the relative position of the starting point and the end point, but not to the path from the starting point to the end point.
There is another feature of potential energy. The absolute value of potential energy often depends on the set zero potential energy point, but no matter where the zero potential energy point is set, the difference of potential energy between two points is certain.
Let's get back to the point.

code
Because you want to run bellman ford, you need to record the edge, make up a point 0, and make the distance from 0 to all other points 0,
Run bellman ford
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
cin >> a[i].u >> a[i].v >> a[i].power;
}
int Bellman()
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (dis[a[j].v] > dis[a[j].u] + a[j].power)
dis[a[j].v] = dis[a[j].u] + a[j].power;
}
}
int judge = 1;//Determine whether there is a negative ring
for (int j = 1; j <= m; j++)
{
if (dis[a[j].v] > dis[a[j].u] + a[j].power)
{
judge = 0;
break;
}
}
return judge;
}
2. Modify the weight of each edge and record the distance from the source point 0 to other points, which will be used later
for (int i = 1; i <= m; i++)
{
a[i].power = a[i].power + dis[a[i].u] - dis[a[i].v];
}
for (int i = 1; i <= n; i++)
dis1[i] = dis[i];
3. Build the heap and run it n times dijkstra
for (int i = 1; i <= m; i++)
{
p.u = a[i].u;//There's no need to write this
p.v = a[i].v; p.power = a[i].power;
mp[a[i].u].push_back(p);
}
for (int i = 1; i <= n; i++)
{
dijis(i);
}
void dijis(int x)
{
memset(book, 0, sizeof(book));
for (int i = 1; i <= n; i++)
dis[i] = Max;
dis[x] = 0;
priority_queue<node> q;
p.u = x; p.v = x;
p.power = 0;
q.push(p);
while (!q.empty())
{
node now = q.top(); q.pop();
if (book[now.v] == 1)
continue;
int y = now.v;
book[y] = 1;
int len = mp[y].size();
for (int i = 0; i < len; i++)
{
if (dis[mp[y][i].v] > dis[y] + mp[y][i].power)
{
dis[mp[y][i].v] = dis[y] + mp[y][i].power;
p.u = y; p.v = mp[y][i].v;
p.power = dis[mp[y][i].v];
q.push(p);
}
}
}
long long ans = 0;
//If dis[i] = = infinite, node x cannot reach node I,
//There is no need to restore dis[i]
for (int i = 1; i <= n; i++)
{
if(dis[i]!=Max)
dis[i] = dis[i] - dis1[x] + dis1[i];
}
for (int i = 1; i <= n; i++)
{
ans += i * dis[i];
}
cout << ans << endl;
}