Algorithms Series 15 Days Quick - Sixth Days Five Classics Search

From: http://blog.csdn.net/m13666368773/article/details/7516439

Do you feel that trees are prevalent in the data structure, and that every field should be touched and touched?

Take the sort we learned a few days ago and use the heap and today's "binary sort tree," so radically say, master the tree you are a cowman.

Today I'm going to talk about the "Find the Last Binary Sorting Tree" of the five classics.

1. concept:

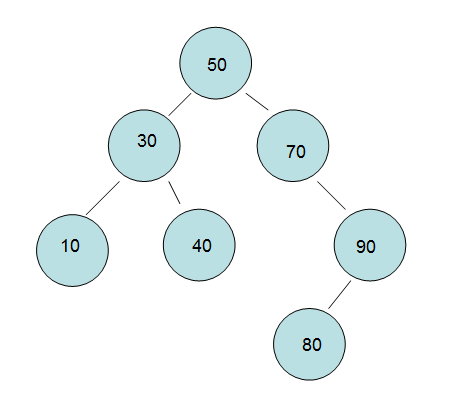
In fact, <1> is very simple. If the root node has a left subtree, all the nodes of the left subtree are smaller than the root node.

If the root node has a right subtree, all nodes of the right subtree are larger than the root node.

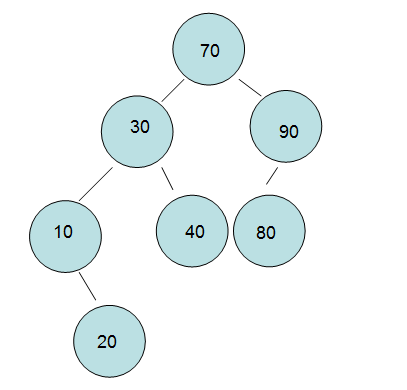
The <2> figure is a "binary sort tree", and then compare with the concept.

2. Actual operation:

As we all know, to operate a thing is nothing more than adding, deleting, checking and modifying. Next, we will talk about the basic operation.

<1> Insertion: I believe you all know the concept of "sort tree", then the principle of insertion is very simple.

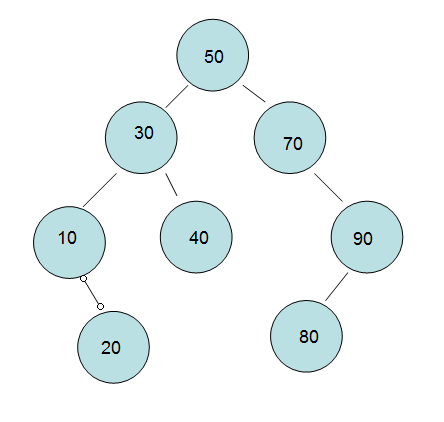
Let's say we insert a 20 into the tree.

First of all, 20 to 50 ratio, found that 20 is old and young, had to be boiled down to 50 left subtrees to compare.

Then: 20 to 30, we find that 20 is still young and old.

Then: 20 to 10, find yourself the eldest, and insert it into the right subtree of 10.

Finally, the effect rendering chart is as follows:

Finding: Believe that if you understand insertion, it's easy to understand.

Take the picture above, for example, I want to find node 10.

First of all, when 10 is compared with 50, it is found that 10 is young and old, and it is found in the left subtree of 50.

Then: 10 to 30, if you find that you are old or young, look in the left subtree of 30.

Then: 10 to 10, find the same, and then return to the signal found.

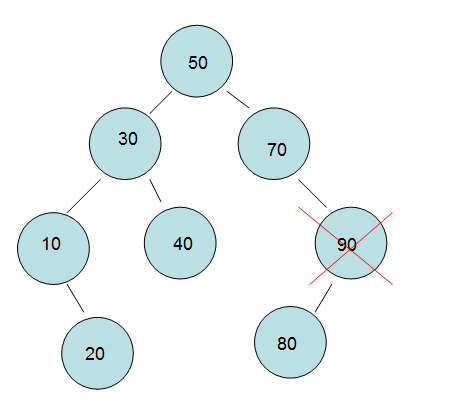
Delete < 3 >: Delete nodes in the tree is more troublesome, there are three main cases.

Delete "leaf node 20" in "1". This situation is relatively simple. Delete 20 will not destroy the structure of the tree. As shown in the picture:

In "2" delete "single child node 90", which is a little more troublesome than the first one, and need to put his child on top.

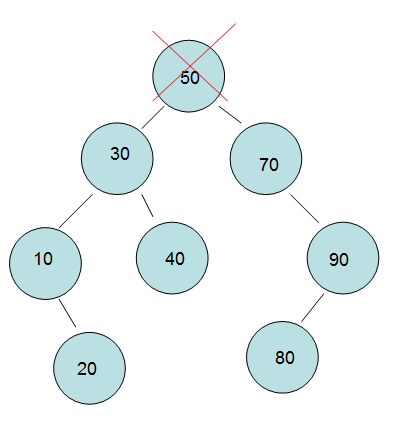
The deletion of "50 nodes for both right and left children" in "3" has made me tangle with coding for a long time, and the problem is very straightforward.

I deleted 50. Who had the problem, the left child? Or the right child? Or something else? Here I will

Frankly, I don't know if you know the middle order traversal of the binary tree, but I'll talk about it later. Now it's OK.

Keep in mind that the formula is to find the left child of the left subtree of the right node.

For example, first find 50 right children, 70.

Then find the leftmost child of 70 and return to him if he finds none.

Finally, the original and final drawings are as follows.

3. Having said so much, talk to the code.

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

using System.Diagnostics;



namespace TreeSearch

{

     class Program

     {

         static void Main(string[] args)

         {

             List<int> list = new List<int>() { 50, 30, 70, 10, 40, 90, 80 };



             //Create a binary traversal tree

             BSTree bsTree = CreateBST(list);



             Console.Write("The raw data of intermediate traversal:");



             //Sequential traversal

             LDR_BST(bsTree);



             Console.WriteLine("\n---------------------------------------------------------------------------n");



             //Find a node

             Console.WriteLine("\n10 Is it included in the binary tree?" + SearchBST(bsTree, 10));



             Console.WriteLine("\n---------------------------------------------------------------------------n");



             bool isExcute = false;



             //Insert a node

             InsertBST(bsTree, 20, ref isExcute);



             Console.WriteLine("\n20 After inserting into the binary tree and traversing in middle order:");



             //Sequential traversal

             LDR_BST(bsTree);



             Console.WriteLine("\n---------------------------------------------------------------------------n");



             Console.Write("Delete leaf nodes 20， \n After middle order traversal:");



             //Delete a node (leaf node)

             DeleteBST(ref bsTree, 20);



             //Again intermediate traversal

             LDR_BST(bsTree);



             Console.WriteLine("\n****************************************************************************\n");



             Console.WriteLine("Delete single-child nodes 90， \n After middle order traversal:");



             //Delete single-child nodes

             DeleteBST(ref bsTree, 90);



             //Again intermediate traversal

             LDR_BST(bsTree);



             Console.WriteLine("\n****************************************************************************\n");



             Console.WriteLine("Delete the root node 50， \n After middle order traversal:");

             //Delete the root node

             DeleteBST(ref bsTree, 50);



             LDR_BST(bsTree);



         }



         ///<summary>

/// Define a binary sort tree structure

///</summary>

         public class BSTree

         {

             public int data;

             public BSTree left;

             public BSTree right;

         }



         ///<summary>

/// Insertion of Binary Sorting Tree

///</summary>

/// <param-name="bsTree">sort tree</param>

/// <param-name="key">insertion number </param>

/// Whether the if statement </param> has been executed by <param name="isExcute">

         static void InsertBST(BSTree bsTree, int key, ref bool isExcute)

         {

             if (bsTree == null)

                 return;



             //If the parent node is larger than key, traverse the left subtree

             if (bsTree.data > key)

                 InsertBST(bsTree.left, key, ref isExcute);

             else

                 InsertBST(bsTree.right, key, ref isExcute);



             if (!isExcute)

             {

                 //Building the current node

                 BSTree current = new BSTree()

                   {

                       data = key,

                       left = null,

                       right = null

                   };



                 //The current element inserted into the parent node

                 if (bsTree.data > key)

                     bsTree.left = current;

                 else

                     bsTree.right = current;



                 isExcute = true;

             }



         }



         ///<summary>

/// Creating Binary Sorting Tree

///</summary>

///<param name="list"></param>

         static BSTree CreateBST(List<int> list)

         {

             //Building Root Node in BST

             BSTree bsTree = new BSTree()

             {

                 data = list[0],

                 left = null,

                 right = null

             };



             for (int i = 1; i < list.Count; i++)

             {

                 bool isExcute = false;

                 InsertBST(bsTree, list[i], ref isExcute);

             }

             return bsTree;

         }



         ///<summary>

/// Search for a specified node in a sorted binary tree

///</summary>

///<param name="bsTree"></param>

///<param name="key"></param>

///<returns></returns>

         static bool SearchBST(BSTree bsTree, int key)

         {

             //If bsTree is empty, the traversal is over

             if (bsTree == null)

                 return false;



             if (bsTree.data == key)

                 return true;



             if (bsTree.data > key)

                 return SearchBST(bsTree.left, key);

             else

                 return SearchBST(bsTree.right, key);

         }



         ///<summary>

/// Mid-Rank Traversal Binary Sorting Tree

///</summary>

///<param name="bsTree"></param>

///<returns></returns>

         static void LDR_BST(BSTree bsTree)

         {

             if (bsTree != null)

             {

                 //Traversing Left Subtree

                 LDR_BST(bsTree.left);



                 //Input node data

                 Console.Write(bsTree.data + "");



                 //Traversing right subtree

                 LDR_BST(bsTree.right);

             }

         }



         ///<summary>

/// Delete the specified key node in the binary sorting tree

///</summary>

///<param name="bsTree"></param>

///<param name="key"></param>

         static void DeleteBST(ref BSTree bsTree, int key)

         {

             if (bsTree == null)

                 return;



             if (bsTree.data == key)

             {

                 //The first case: leaf nodes

                 if (bsTree.left == null && bsTree.right == null)

                 {

                     bsTree = null;

                     return;

                 }

                 //The second case is that the left subtree is not empty

                 if (bsTree.left != null && bsTree.right == null)

                 {

                     bsTree = bsTree.left;

                     return;

                 }

                 //In the third case, the right subtree is not empty

                 if (bsTree.left == null && bsTree.right != null)

                 {

                     bsTree = bsTree.right;

                     return;

                 }

                 //In the fourth case, neither left nor right subtree is empty.

                 if (bsTree.left != null && bsTree.right != null)

                 {

                     var node = bsTree.right;



                     //Find the leftmost node in the right subtree

                     while (node.left != null)

                     {

                         //Traversing its left subtree

                         node = node.left;

                     }



                     //Exchange left and right children

                     node.left = bsTree.left;



                     //Judging whether it is a true leaf node or a parent of an empty left child

                     if (node.right == null)

                     {

                         //Delete the leftmost node of the right subtree

                         DeleteBST(ref bsTree, node.data);



                         node.right = bsTree.right;

                     }

                     //Re-assignment

                     bsTree = node;



                 }

             }



             if (bsTree.data > key)

             {

                 DeleteBST(ref bsTree.left, key);

             }

             else

             {

                 DeleteBST(ref bsTree.right, key);

             }

         }

     }

}

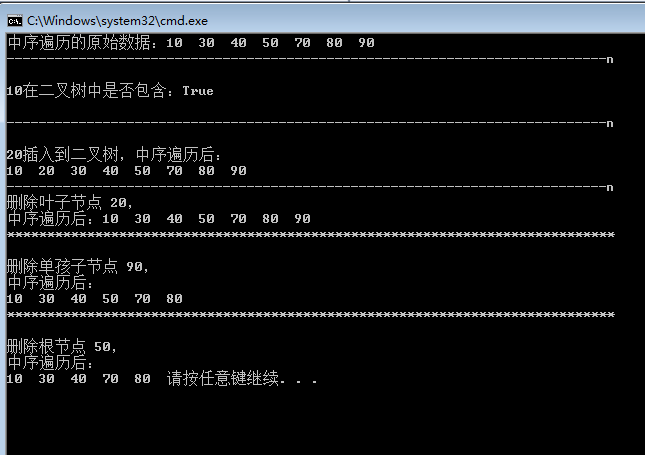
Operation results:

Note that the binary sorting tree also uses the "space for time" approach.

Suddenly found that the middle order traversal of binary sort tree can also sort arrays, ha ha ha, good!

PS: Insert operation: O(LogN).

Delete operation: O(LogN).

Find operation: O(LogN).

Posted by dan90joe on Sat, 18 May 2019 16:33:26 -0700

Programmer Group

Algorithms Series 15 Days Quick - Sixth Days Five Classics Search

Algorithms Series 15 Days Quick - Sixth Days Five Classics Search

Hot Keywords