Title Description:

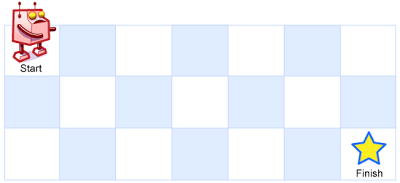
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

Note: m and n will be at most 100.

Topic analysis:

We can use count[i][j] to express how many kinds of walking methods there are on the space of column J in row I. After analysis, there will be the following relationship:
count[i][j] = count[i - 1][j] + count[j][i - 1]
With the recursive relation, the solution of this problem can be easily realized.

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> count(m,vector<int>(n,1));
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                count[i][j] = count[i - 1][j] + count[i][j - 1];
            }
        }
        return count[m - 1][n - 1];
    }
};

The time complexity of the above solution is O(mn), and the space complexity is O(mn). But in fact, the above solution only involves two lines, so the space complexity of the above algorithm can be simplified to O(n):

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> count1(n, 1);
        vector<int> count2(n, 1);
        for(int i = 1; i < m; i++){
            if(i % 2){
                add(count2, count1);
            }else{
                add(count1, count2);
            }
        }
        return max(count1[n - 1], count2[n - 1]);
    }
    void add(vector<int>& counta, vector<int>& countb){
        for(int i = 1; i < counta.size(); i++){
            counta[i] = counta[i - 1] + countb[i];
        }
    }
};

Looking at the above code carefully, you can see that you can actually use an array to accomplish tasks, thus simplifying the code:

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> count(n, 1);
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                count[j] = count[j - 1] + count[j];
            }
        }
        return count[n - 1];
    }
};