Algorithm | traversing binary search tree

Another contribution from my good friend Evil Say, the following is the original text:

1. Basic Definitions

Each sub-node of the binary search tree has at most two leaf nodes
Each node of the binary search tree has at most one root node.
Stored elements must be comparable
Value of each sub-node of the binary search tree
- Values greater than all nodes in its left subsection
- Values of all nodes smaller than their right subnodes
Bipartite search trees are not necessarily full

2. Java Implementation of Binary Search Tree

/**
 * @Author: EvilSay
 * @Date: 2019/8/6 19:00
 */
public class BSTMain <E extends Comparable<E>> {
    private class Node {
        public E e;
        private Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    //root node
    private Node root;
    private int size;

    public BSTMain() {
        root = null;
        size = 0;
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }
    public void add(E e){

        root = add(this.root, e);

    }

    // A recursive algorithm for inserting element E into a binary search tree with node as its root
    // Returns the root of the binary search tree after inserting a new node
    private Node add(Node node, E e){

        if (node == null){

            size ++;
            return new Node(e);
        }

        if (e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if (e.compareTo(node.e) > 0)
            node.right = add(node.right,e);
        return node;
    }

    // See if the binary search tree contains element e
    public boolean contains(E e){
        return contains(root,e);
    }

    // Recursive algorithm to see whether the binary search tree with node as its root contains element e
    private boolean contains(Node node, E e){
        if (node == null)
            return false;
        if (e.compareTo(node.e) == 0)
            return true;
        else if (e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else
            return contains(node.right,e);
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        generateBSTSString(root,0,res);
        return res.toString();
    }

    // Generate string describing binary tree with node as root node and depth as depth
    private void generateBSTSString(Node root, int depth, StringBuilder res) {
        if (root == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }
        res.append(generateDepthString(depth) + root.e + "\n");
        generateBSTSString(root.left, depth + 1 ,res);
        generateBSTSString(root.right, depth + 1, res);

    }

    private String generateDepthString(int depth) {
        StringBuilder res = new StringBuilder();
        for (int i = 0; i < depth; i++)
            res.append("--");
        return res.toString();
    }
}

3. Graphical Binary Search Tree

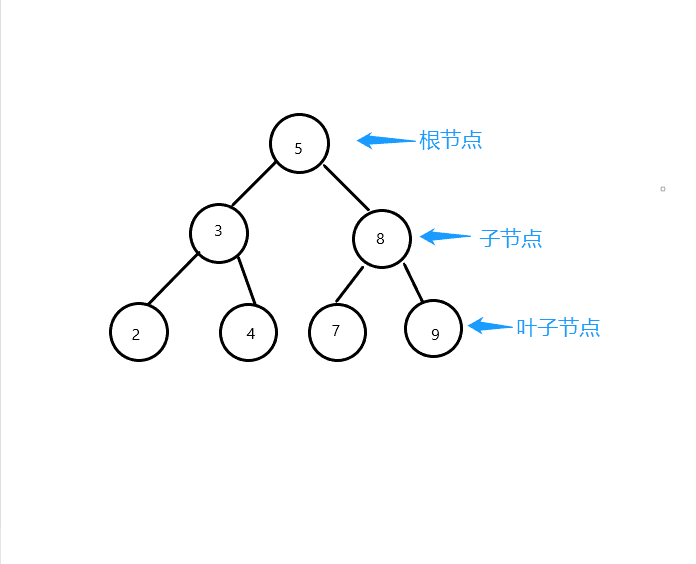
From the graph, we can see that the value of each node in the binary search tree is larger than that of all nodes in its left sub-section and smaller than that of all nodes in its right sub-node.

4. Preorder traversal

Pre-order traversal is also known as pre-order traversal. The order of access is about the root, that is, to access the root node first, then to the left subtree, and finally to the right subtree. So the order of access shown above is 5, 3, 2, 4, 8, 7, 9.

Preorder Traversal of Binary Search Tree Recursive Version and Non-Recursive Version

    //Pre-order traversing binary search tree rooted by node, recursive algorithm
    private void preOrder(Node node){

        if (node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }
    
    //Preorder Traversal Recursive Call of Binary Search Tree
    public void preOrder(){
        preOrder(root);
    }
    
    //Preorder Traversal Non-recursive Writing of Binary Search Trees
    public void preOrderNG(){
        Stack<Node> stack = new Stack<>();
        //root node
        stack.push(root);

        while (!stack.isEmpty()){
            Node cur = stack.pop();

            System.out.println(cur.e);
            //Determine whether there are leaf nodes
            if (cur.right != null)
                stack.push(cur.right);
            if (cur.left != null)
                stack.push(cur.left);
        }
    }

Understanding the logic of non-recursive implementation and deriving the realization of preceding recursion

Create a stack, we push the root node 5 into the stack, then we will visit the root node 5, all push 5 out of the stack.
The elements rolled out are {5} and the elements in the stack are [].
In the push-in 5 sub-node is 3,8, we first push-in, then push-in 8 and then push-in 3, now the stack elements are [8,3], the top of the stack is the next node we will visit, so push-out 3.
The derived elements are {5,3} and the elements in the stack are [8].
The sub-nodes of push-in 3 are 2,4, push-in first, push-in 4 then push-in 2. Now the elements of the stack are [8,4,2]. The top 2 of the stack is the node we will visit next time, so push-out 2.
The derived elements are {5,3,2} and the elements in the stack are [8,4].
Access the top 4 of the stack because 2 and 4 have no child nodes. So we just pushed 4 out of the top of the stack.
The derived elements are {5,3,2,4} and the elements in the stack are [8].
Visit the top of the stack, push 8 out of the stack, then push 8's sub-nodes 7 and 9 into the stack, first push 9, then push 7.
The derived elements are {5,3,2,4,8} and the elements in the stack are [9,7].
Access 7, no child nodes, launch.
The derived elements are {5,3,2,4,8,7} and the elements in the stack are [9].
Access 9, no child nodes, launch.
The derived elements are {5,3,2,4,8,7,9} and the elements in the stack are [].

5. Mid-order traversal

Intermediate traversal, access order is left root right, that is, access to the left subtree, then to the root node, and finally to the right subtree. So the order of access shown above is 2, 3, 4, 5, 7, 8, 9.

Ordered traversal recursive version and non-recursive version in binary search tree

    //Recursive call
    public void inOrder(){
        inOrder(root);
    }
    //Recursive Writing of Bipartite Search Tree with Mid-Rank Traversal
    private void inOrder(Node root){
        if (root == null)
            return;

        inOrder(root.left);
        System.out.println(root.e);
        inOrder(root.right);
    }
    //Ordered traversal to recursive writing in binary search tree
    public void preInOrderNG(){
        // Create stacks, similar to preface traversal
        Stack<Node> stack = new Stack<>();
        
        Node node = root;
        //Add the temporary end and start the pop element
        while(node!=null || stack.size()>0 ){

            while(node!=null){
                stack.push(node);
                node = node.left;
            }
            //While pop and judgment, the right node will not null, the right subtree, continue to add all the left-most nodes in accordance with the addition method.
            if(stack.size()>0){
                Node pop = stack.pop();
                System.out.print(pop.e+"  ");
                if(pop.right!=null){
                    node = pop.right;
                }
            }
        }

Understanding the Realization Logic of Non-recursion and Derivating the Realization of Mid-order Recursion

Firstly, we push 5 nodes into the stack, then 3 left sub-nodes of 5, 2 left sub-nodes of 3, and 2 left sub-nodes of 2 (at this time, the left sub-nodes of 2 are empty, node= null while loop exits).
The derived elements are {} and the elements in the stack are [5, 3, 2].
The node is empty, but there are elements in our stack, accessing the top element 2 of the stack, and checking whether 2 has a right child node. If not, roll out the stack and end the loop.
The derived elements are {2} and the elements in the stack are [5,3].
Access the top element 3 of the stack, push 3 out of the stack, and push the right child node 4 of 3 into the stack to end the cycle.
The derived elements are {2,3} and the elements in the stack are [5].
Access the top element 5 and push 5 out of the stack. Push the right sub-node 8 of 5 into the stack, and the left sub-node 7 of 8 into the stack to end the cycle.
The derived elements are {2,3,5} and the elements in the stack are [8,7]
Access the top element 7 of the stack and see if 2 has a right child node. If not, roll out the stack and end the loop.
The derived elements are {2,3,5,7} and the elements in the stack are [8].
Access the top element 8 and push 8 out of the stack. Push the right child node 9 of 8 into the stack
The derived elements are {2,3,5,7,8} and the elements in the stack are [9].
Access the top element 9 of the stack and see if 2 has a right child node. If not, roll out the stack and end the loop.
The derived elements are {2,3,4,5,7,8,9} and the elements in the stack are [].

6. Postorder traversal

Intermediate order traversal, access order is left and right root, that is, first access to the left subtree, then to the right subtree, and finally to the root node. So the order of access shown above is 2, 4, 3, 7, 9, 8, 5.

Binary Search Tree Post-order Traversal of Recursive Version and Non-Recursive Version

//Recursive call
public void postOrder() {
    postOrder(root);
} 

//A Postorder Traversal Recursive Method for Binary Search Trees
private void postOrder(Node node){
    if (node == null)
        return;

    postOrder(node.left);
    postOrder(node.right);
    System.out.println(node.e);
} 

public void postOrderNG(){
    Stack<Node> stack = new Stack<>();
    //Use a list collection to record the root nodes that have been traversed to prevent a dead cycle
    ArrayList<Node> list = new ArrayList<>();
    Node node = root;
    Node proud; 
    int flag; 

    //The first page checks the left subtree of the tree, then the right subtree, and finally outputs the root node.
    while (node != null || stack.size() > 0){
        //Complete adding the leftmost subtree
        while (node != null){
            stack.push(node);

            node = node.left;
        } 

        //Similar to sequential traversal, in order to output the left sub-node first, but after the output of the node, the root node cannot be ejected directly, but the right node must be ejected first.
        //Finally, if the root node pops up again, it will involve the question of whether the access status of a root node has been traversed.
        if (stack.size() > 0){

            Node peek = stack.peek();
            if (peek.right != null){
                boolean con = list.contains(peek);
                if (con){
                    Node pop = stack.pop();
                    System.out.println(pop.e);
                }else{
                    list.add(peek);
                    node = peek.right;
                }
            }else {
                Node pop = stack.pop();
                System.out.println(pop.e);
            }

        }

    }
}

Understanding the logic of non-recursive implementation and deriving the realization of sequential recursion

Push 5 into the stack, 3 into the left child node of 5, 2 into the left child node of 3, and 2 into the left child node of 2 (at this time, the left child node of 2 is empty, node= null while loop exits).
The derived elements are {} and the elements in the stack are [5, 3, 2].
The node is empty, but there are elements in our stack. Access the top element 2 of the stack and see if there are left child nodes in 2. If not, roll out the stack and end the loop.
The derived elements are {2} and the elements in the stack are [5,3].
Access the right subsection of the top element 3 and 3 of the stack is 4 to determine whether there is 3 in the list, and if not, put 3 in the list and assign node to 4 to end the loop.
The derived elements are {2} and the elements in the stack are [5,3].
Node 4, push 4 into the stack, and access the top element 4, and see if 4 has a right child node. If not, roll out the stack and end the loop.
The derived elements are {2,4} and the elements in the stack are [5,3].
Access the top element 3 of the stack, there are 3 in the list, push 3 out of the stack and end the loop.
The derived elements are {2,4,3} and the elements in the stack are [5].
Accessing the right subsection of the top element 5 and 5 of the stack is 8 to determine whether there is 8 in lis t, or not, putting 5 in the list and assigning node to 8 to end the loop.
The derived elements are {2,4,3} and the elements in the stack are [5].
Node is 8, pushing 8 into the stack and accessing the top element 8. 8 has a left child node of 7. Push 7 into the stack.
The derived elements are {2,4,3} and the elements in the stack are [5,8,7].
Access the top element 7 of the stack and see if 7 has a right child node. If not, roll out the stack and end the loop.
The derived elements are {2,4,3,7} and the elements in the stack are [5,8].
The right child of accessing the top element 8 and 8 of the stack is 9. Determine if there is 9 in the list, and if not, put 8 in the list and assign node to 9 to end the loop.
The derived elements are {2,4,3,7} and the elements in the stack are [5,8].
The node is 9, pushes 9 into the stack, accesses the top element 9, and checks whether 9 has a right child node. If not, roll out the stack and end the loop.
The derived elements are {2,4,3,7,9} and the elements in the stack are [5,8].
Access the top element 8 of the stack, 8 in the list, push 8 out of the stack and end the loop.
The derived elements are {2,4,3,7,9,8} and the elements in the stack are [5].
node is also an element in the empty stack, accessing the top element 5 of the stack, 5 in the list, pushing 5 out of the stack and ending the loop.
The derived elements are {2,4,3,7,9,8,5} and the elements in the stack are [].

Programmer Group