33. Search rotation sort array - medium - 9 / 17
33. Search rotation sort array - medium
The integer array nums is arranged in ascending order, and the values in the array are different from each other.
Before passing to the function, Num rotates on a previously unknown subscript k (0 < = k < num.length), making the array [num [k], Num [K + 1],..., Num [n-1], Num [0], Num [1],..., Num [k-1]] (subscripts count from 0). For example, [0,1,2,4,5,6,7] may become [4,5,6,7,0,1,2] after rotation at subscript 3.
Give you the rotated array num and an integer target. If the target value target exists in num, return its subscript, otherwise return - 1.


Solution 1:
Direct traversal search
class Solution {
public int search(int[] nums, int target) {
int len = nums.length;
int i=0;
while(i<len){
if(nums[i] == target){
return i;
}
i++;
}
return -1;
}
}
Solution 2:
Binary search: divide the array into left and right halves to determine which part is ordered, and then judge whether the target is within the range in the ordered part. Continue binary search to narrow the range, and search in the other half if it is not.
class Solution {
public int search(int[] nums, int target) {
int right = nums.length-1; //Right pointer
if(right<0) return -1;
if(right == 0) return nums[0]==target? 0:-1;
int left = 0; //Left pointer
int mid = 0; //Median subscript
while(left<=right){
mid = (left+right)/2; //Calculate median
if(nums[mid] == target) return mid;
if(nums[left] <= nums[mid]){ //Left half ordered
if(target >= nums[left] && target < nums[mid]){ //target is on the left half
right = mid - 1;
}else{
left = mid + 1;
}
}else{ //Right half ordered
if(target > nums[mid] && target <= nums[right]){//target is on the right half
left = mid + 1;
}else{
right = mid - 1;
}
}
}
return -1;
}
}
34. Find the first and last position of an element in a sorted array - medium - 9 / 18
34. Find the first and last position of an element in a sorted array - medium - 9 / 18
Given an integer array nums arranged in ascending order and a target value target. Find the start and end positions of the given target value in the array.
If the target value target does not exist in the array, return [- 1, - 1].
Advanced:
- Can you design and implement an algorithm with time complexity of O(log n) to solve this problem?


Resolution:
The l pointer is in charge of the left blue area and the rr pointer is in charge of the right red area. The two do not conflict with each other. Expand the control area by constantly approaching the target element until the two control areas border.
Binary search start status:
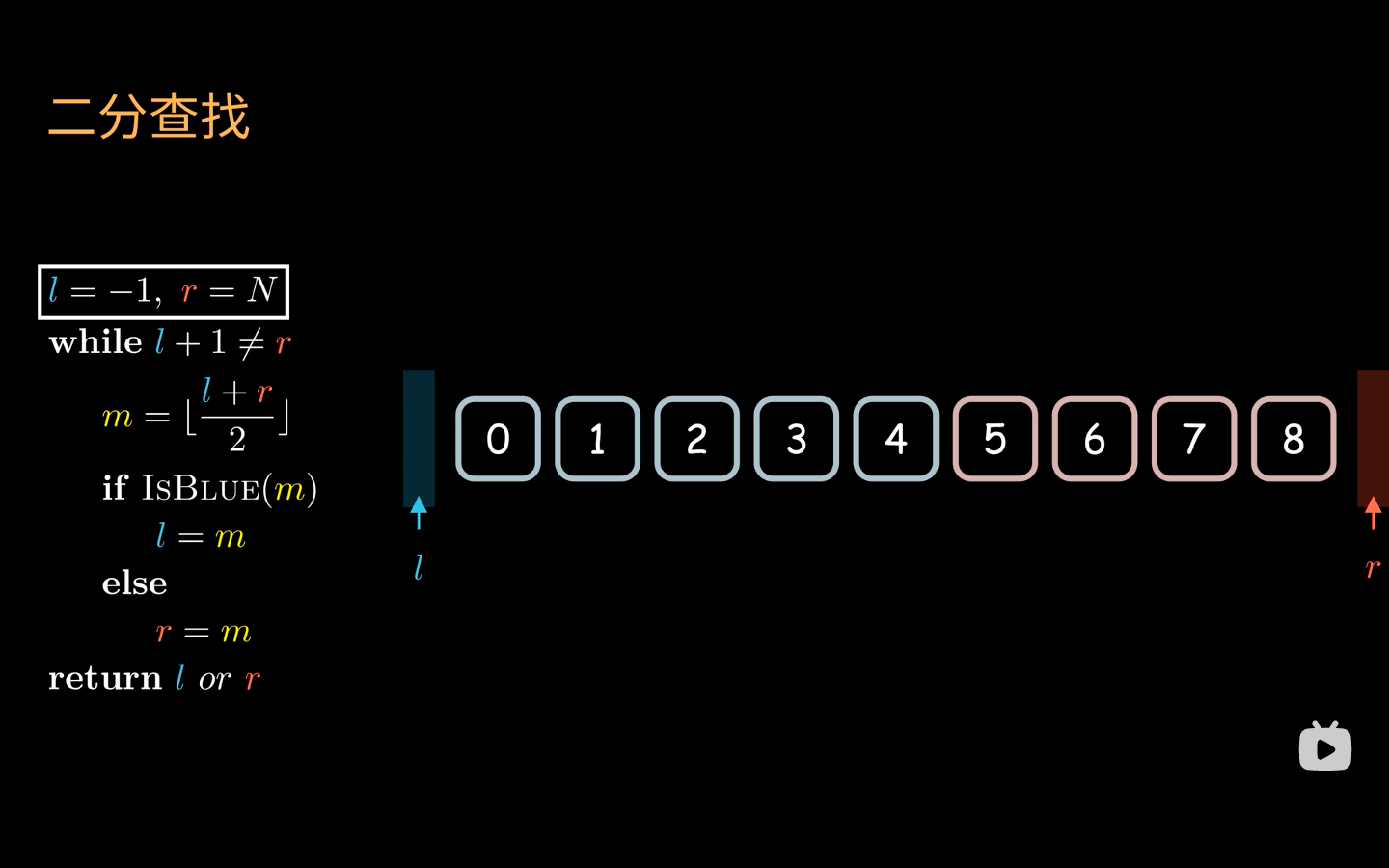
Binary search termination status:

Division of blue and red regions corresponding to <, ≤, ≥, > target elements

Summary template:

class Solution {
public int[] searchRange(int[] nums, int target) {
//Left boundary
int leftIdx = binarySearchLeft(nums, target);
//Right boundary
int rightIdx = binarySearchRight(nums, target);
//Judge whether it meets the requirements
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
return new int[]{leftIdx, rightIdx};
}
return new int[]{-1, -1};
}
//Find left boundary binary search
public int binarySearchLeft(int[] nums, int target) {
//Note the initial value of the left and right pointers
int left = -1, right = nums.length;
while (left+1 != right) {
int mid = (left + right) / 2;
if (nums[mid] >= target) {
right = mid;
} else {
left = mid;
}
}
return right;
}
//Find the binary search of the right boundary
public int binarySearchRight(int[] nums, int target) {
//Note the initial value of the left and right pointers
int left = -1, right = nums.length;
while (left+1 != right) {
int mid = (left + right) / 2;
if (nums[mid] <= target) {
left = mid;
} else {
right = mid;
}
}
return left;
}
}
Time complexity: O (log (n)).
Space complexity: O (1).
39. Combined sum - medium - 9 / 22
39. Combined sum - medium - 9 / 22
Given a positive integer array of candidates without duplicate elements and a positive integer target, find all the unique combinations in candidates that can make the number and target the target number.
The number in candidates can be selected repeatedly without limit. If the number of at least one selected number is different, the two combinations are unique.
For a given input, the number of unique combinations of guaranteed sum and target is less than 150.


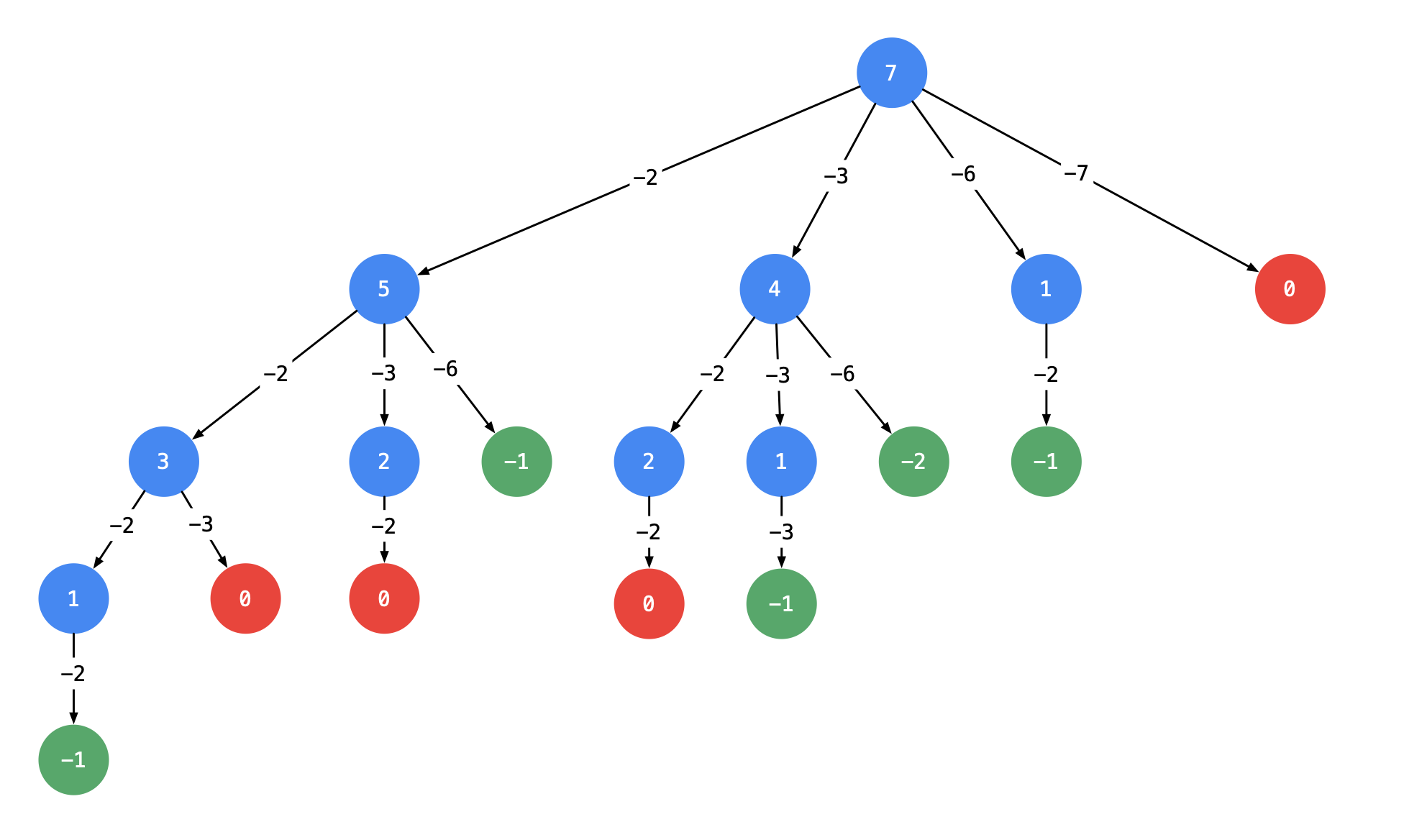

Resolution:
List all the situations ahead, and go back when you get a solution or can't get through.
class Solution {
List<List<Integer>> res;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
//Storage results
res = new ArrayList<>();
//sort
Arrays.sort(candidates);
//to flash back
backtrack(candidates,target,new ArrayList<>(),0);
return res;
}
//to flash back
private void backtrack(int[] candidates,int remains,List<Integer> path,int start){
//If 0 remains after subtraction, add this path
if(remains == 0){
res.add(new ArrayList<>(path));
return;
}
//ergodic
for(int i=start; i<candidates.length; i++){
//Returns if the remaining value is less than 0
if(remains-candidates[i] < 0) return;
//Pruning is to remove the same number of paths, such as [2,2,3,7] to remove the second 2.
if(i > 0 && candidates[i] == candidates[i-1]) continue;
//Add element to path
path.add(candidates[i]);
//to flash back
backtrack(candidates, remains-candidates[i], path, i);
//A solution is found or remains < 0. Remove the current number and continue trying
path.remove(path.size()-1);
}
}
}

42. Rainwater connection - difficult - 9 / 23
42. Rainwater connection - difficult - 9 / 23
Given n non negative integers to represent the height diagram of each column with width 1, calculate how much rain the columns arranged according to this can receive after rain.


Method 1: double pointer

class Solution {
public int trap(int[] height) {
int left = 0, right = height.length - 1; //Define left and right pointers
int ans = 0; //result
int left_max = 0, right_max = 0; //Left and right current maximum
while(left<right){
if(height[left] < height[right]){ //If the height on the left is less than that on the right
if (height[left] >= left_max){ //If the current value on the left is greater than or equal to the maximum value on the left, the maximum value on the left is updated
left_max = height[left];
} else { //Otherwise, the rainwater volume can be accumulated and calculated
ans += (left_max - height[left]);
}
++left; //Move left pointer
} else { //If the height on the left is greater than that on the right
if(height[right] >= right_max){ //If the current value on the right is greater than or equal to the maximum value on the right, the maximum value on the right is updated
right_max = height[right];
} else { //Otherwise, the rainwater volume can be accumulated and calculated
ans += (right_max - height[right]);
}
--right; //Move right pointer
}
}
return ans;
}
}
Time complexity: O(n).
Space complexity: O(1).
Method 2: dynamic programming
class Solution {
public int trap(int[] height) {
int len = height.length; //length
if(len == 0){
return 0;
}
//Traverse from left to right and record the highest value on the left
int[] left_max = new int[len];
left_max[0] = height[0];
for(int i=1; i<len; i++){
left_max[i] = Math.max(left_max[i-1],height[i]);
}
//Traverse from right to left and record the highest value on the right
int[] right_max = new int[len];
right_max[len-1] = height[len-1];
for(int j=len-2; j>=0; j--){
right_max[j] = Math.max(right_max[j+1],height[j]);
}
//Calculated water intake
int sum = 0;
for(int k=0; k<len; k++){
sum += Math.min(left_max[k],right_max[k]) - height[k];
}
return sum;
}
}
Time complexity: O(n), where n is the length of the array height. It is necessary to traverse the array height once to calculate the element values of the arrays leftMax and rightMax, and once to calculate the total amount of rainwater that can be received.
Space complexity: O(n), where n is the length of the array height. You need to create two arrays of length N, leftMax and rightMax.
46. Full alignment - medium - 9 / 24
Given an array num without duplicate numbers, returns all possible permutations. You can return answers in any order.

Analysis: backtracking method
Use recursion to add a number to temp each time. When the number is added enough, come back for backtracking, and then add a new solution backward.
It can be understood as adding layer by layer. Each layer is a for loop.

Each call layer enters a for loop, which is equivalent to listing all solutions, and then selecting what we need. In fact, it is essentially depth first traversal of DFS.
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> res = new ArrayList<>(); //Storage results
backtrack(nums,res,new ArrayList<>()); //to flash back
return res; //Return results
}
private void backtrack(int[] nums,List<List<Integer>> res, List<Integer> tempList){
if(tempList.size() == nums.length){ //If the length of the temporary list is equal to the length of the array, it is added and returned
res.add(new ArrayList<>(tempList));
return;
}
for(int i=0; i<nums.length; i++){
if(tempList.contains(nums[i])) continue; //If the element already exists, skip
tempList.add(nums[i]); //Add element
backtrack(nums,res,tempList); //Continue adding backward
tempList.remove(tempList.size() - 1); //Remove the newly added element of tempList and try a new element
}
}
}
analysis:
Before recursion => [1] Before recursion => [1, 2] Before recursion => [1, 2, 3] After recursion => [1, 2] After recursion => [1] Before recursion => [1, 3] Before recursion => [1, 3, 2] After recursion => [1, 3] After recursion => [1] After recursion => [] Before recursion => [2] Before recursion => [2, 1] Before recursion => [2, 1, 3] After recursion => [2, 1] After recursion => [2] Before recursion => [2, 3] Before recursion => [2, 3, 1] After recursion => [2, 3] After recursion => [2] After recursion => [] Before recursion => [3] Before recursion => [3, 1] Before recursion => [3, 1, 2] After recursion => [3, 1] After recursion => [3] Before recursion => [3, 2] Before recursion => [3, 2, 1] After recursion => [3, 2] After recursion => [3] After recursion => [] Output results:[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
