Quick sort

Algorithm idea: select a number in the array x x x. Make all > = x >=x >=The number of X is on the right, < = x <=x The number of < = x is on the left and x x x is placed where it should be after sorting, and then the left and right sides are processed recursively until all numbers are placed in the correct position.
Boundary problem: when there are only two numbers, select x x When x, pay attention to whether there is a left boundary or a boundary. If it is a left boundary, then i i i points to the left boundary and is selected during recursion[ i − 1 i - 1 i−1， r r r] It will fall into an endless loop. Similarly, when the right boundary is selected, j j j points to the right boundary and is selected during recursion[ l l l， j j j] It will fall into an endless cycle.
Therefore, select x x When x, the left boundary is used j j j recursion, when taking the right boundary, use i i i recursion
Algorithm implementation:

#include <iostream>
using namespace std;

const int N = 100010;

int q[N];

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    
    while(i < j)
    {
        do i ++; while(q[i] < x);
        do j --; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
    
    return;
}

int main()
{
    int n;
    cin >> n;
    
    for(int i = 0; i < n; i ++) cin >> q[i];
    
    quick_sort(q, 0, n - 1);
    
    for(int i = 0; i < n; i ++) cout << q[i] << ' ';
    
    return 0;
}

Merge sort

Algorithm idea: divide the array into two segments recursively until it is divided into two numbers that can judge the size, then merge, merge the two ordered arrays into an ordered array, and merge upward until the whole array is merged
Algorithm implementation:

#include <iostream>
using namespace std;

const int N = 100010;

int q[N], temp[N];

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    
    int mid = l + r >> 1, i = l, j = mid + 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);
    
    int k = 0;

    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j]) temp[k ++] = q[i ++];
        else temp[k ++] = q[j ++];
        // while(q[i] <= q[j] && i <= mid) temp[k ++] = q[i ++];
        // while(q[j] < q[i] && j <= r) temp[k ++] = q[j ++];
    }
    while(i <= mid) temp[k ++] = q[i ++];
    while(j <= r) temp[k ++] = q[j ++];
    
    for(int i = 0, j = l; j <= r; i ++, j ++) q[j] = temp[i];
    return;
}
int main()
{
    int n;
    cin >> n;
    
    for(int i = 0; i < n; i ++) cin >> q[i];
    
    merge_sort(q, 0, n - 1);
    
    for(int i = 0; i < n; i ++) cout << q[i] << ' ';
    
    return 0;
}

Dichotomy

Algorithmic idea: if a problem has two properties that can be divided into two, we can constantly judge these two properties, update the boundary, and finally find the critical point.
For example:

Given an integer array of length n arranged in ascending order, return the start position and end position of an element k. if the element does not exist in the array, return - 1 - 1.

Boundary problem: when updating the boundary in integer dichotomy, if the left boundary l = m i d l=mid l=mid, then m i d mid mid should be rounded up. When there are only two numbers, if the right boundary is our answer, it will fall into an endless loop. Similarly, it is the same when updating the right boundary. So when we update the left boundary l = m i d l=mid When l=mid, the answer is on the right, so m i d mid mid should be rounded up. When updating the right boundary, it means that the answer is on the left, so m i d mid mid should be rounded down.
Algorithm implementation:

#include <iostream>
using namespace std;

const int N = 100010;

int q[N];

int main()
{
    int n, m;
    cin >> n >> m;
    
    for(int i = 0; i < n; i ++) cin >> q[i];
    
    while (m -- )
    {
        int x;
        cin >> x;
        
        int l = 0, r = n - 1;
        while(l < r)
        {
            int mid = l + r >> 1;
            if(q[mid] >= x) r = mid;
            else l = mid + 1;
        }
        
        if(q[l] != x) cout << "-1 -1" << endl;
        else
        {
            cout << l << ' ';
            l = 0, r = n - 1;
            while(l < r)
            {
                int mid = l + r + 1 >> 1;
                if(q[mid] <= x) l = mid;
                else r = mid - 1;
            }
            cout << l << endl;
        }
    }
    return 0;
}

Prefix and

Algorithm idea: by calculating the prefix sum, we can easily find the sum of a certain interval. We don't need to sum all the numbers in the interval every time, just subtract the prefix sum
One dimensional prefix and: S [ i ] = S [ i − 1 ] + a [ i ] S[i] = S[i - 1] + a[i] S[i]=S[i − 1]+a[i], we define S [ 0 ] = 0 S[0] = 0 S[0]=0
2D prefix and: S [ i , j ] = S [ i − 1 , j ] + S [ i , j − 1 ] − S [ i − 1 , j − 1 ] + a [ i , j ] S[i,j]=S[i-1,j]+S[i,j-1]-S[i-1,j-1]+a[i,j] S[i,j]=S[i − 1,j]+S[i,j − 1] − S[i − 1,j − 1]+a[i,j], similarly, we define S [ 0 , j ] = S [ i , 0 ] = 0 S[0,j] = S[i,0]=0 S[0,j]=S[i,0]=0
Algorithm implementation:
One dimensional prefix sum

Enter a sequence of integers of length n. Next, enter m more queries, and enter a pair of l,r for each query.

#include <iostream>
using namespace std;

const int N = 100010;

int a[N], S[N];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; i ++) 
    {
        scanf("%d", &a[i]);
        S[i] = S[i - 1] + a[i];
    }
    
    while(m --)
    {
        int l, r;
        scanf("%d%d", &l,&r);
        
        printf("%d\n",S[r] - S[l - 1]);
    }
    
    return 0;
    
    
}

2D prefix and

#include <iostream>
using namespace std;

const int N = 1010;

int a[N][N], s[N][N];

int main()
{
    int n, m, q;
    scanf("%d%d%d",&n, &m, &q);
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
        {
            scanf("%d", &a[i][j]);
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
        
    while(q --)
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    
    return 0;
}

Difference

Algorithm idea: by constructing the difference array of the original array, we can add or subtract a value from all the numbers in a certain interval without traversing all the values in this interval. When facing a large number of modification operations, we can O ( 1 ) O(1) O(1)
One dimensional difference: for the original array a [ i ] a[i] a[i], we construct a differential array b [ i ] b[i] b[i], making the original array a [ i ] a[i] a[i] Yes b [ i ] b[i] b[i] the prefix and of the array, i.e a [ i ] = b [ i ] + b [ i − 1 ] + . . . + b [ 1 ] a[i]=b[i]+b[i-1]+...+b[1] a[i]=b[i]+b[i − 1]+...+b[1], when the array a a In a [ l , r ] [l,r] Add or subtract a number from [l,r] c c c only need to b [ l ] + c , b [ r + 1 ] − c b[l] +c,b[r + 1]-c b[l]+c,b[r+1] − c. Construct differential array b [ i ] = a [ i ] − a [ i − 1 ] b[i] = a[i]-a[i-1] b[i]=a[i] − a[i − 1], but in actual construction, it can be considered that all the original arrays are 0 0 0, at this time b b b array is also all 0 0 0, so you only need to consider insertion, a [ i ] a[i] a[i] can be considered as [ i , i ] [i,i] Value inserted at [i,i] a [ i ] a[i] a[i]
Algorithm implementation:
One dimensional difference:

#include <iostream>
using namespace std;

const int N = 100010;

int a[N],b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    int n, m;
    scanf("%d%d",&n,&m);
    
    for(int i = 1; i <= n; i ++) scanf("%d",&a[i]), insert(i, i, a[i]);
    
    while (m -- )
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    
    for(int i = 1; i <= n; i ++) b[i] += b[i - 1], printf("%d ", b[i]);
    
    return 0;
}

Two dimensional difference:

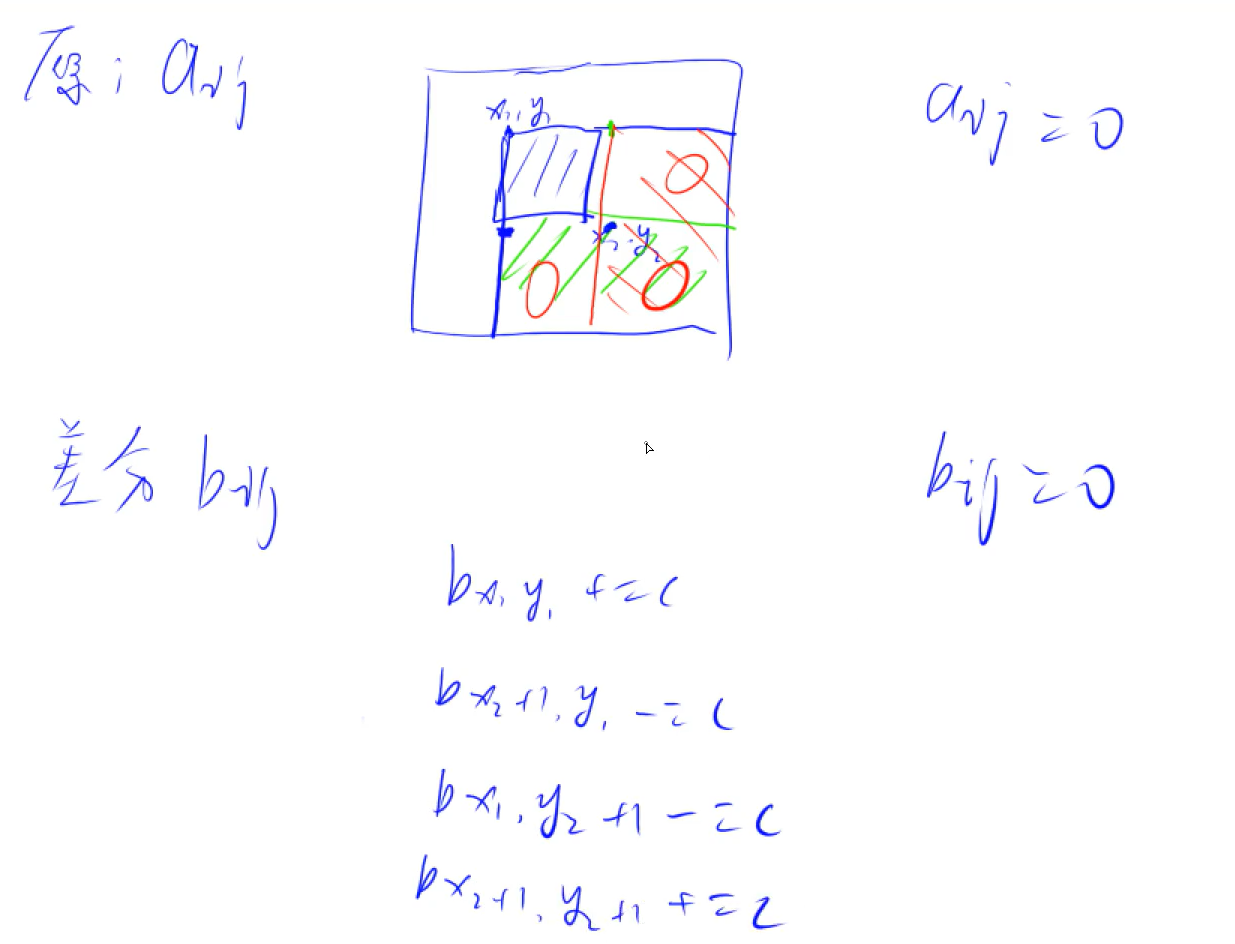
#include <iostream>
using namespace std;

const int N = 1010;

int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    int n, m, q;
    scanf("%d%d%d", &n, &m, &q);
    
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m; j ++)
        {
            scanf("%d", &a[i][j]);
            insert(i, j, i, j, a[i][j]);
        }
    }
    
    while(q --)
    {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        insert(x1, y1, x2, y2, c);
    }
    
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m; j ++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];//Prefix Sum 
            printf("%d ", b[i][j]);
        }
        printf("\n");
    }
    return 0;
    
}

Double pointer algorithm

Algorithmic idea: the double pointer algorithm mainly makes use of some property of the problem, mainly monotonicity O ( n 2 ) O(n^2) The time complexity of O(n2) is optimized to O ( n ) O(n) O(n), which has been used in quick sort and merge sort before.
Algorithm implementation:

Given a sequence of integers with length n, please find the longest continuous interval that does not contain repeated numbers and output its length.

#include <iostream>
using namespace std;

const int N = 100010;

int a[N],s[N];

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i ++) cin >> a[i];
    
    int res = 0;
    for(int i = 0, j = 0; i < n; i ++)
    {
        s[a[i]] ++;
        while(s[a[i]] > 1)
        {
            s[a[j]] --;
            j ++;
        }
        
        res = max(res,  i - j + 1);
    }
    
    cout << res << endl;
    
    return 0;
}

Bit operation

Algorithm idea: bit operation is mainly to find the second in binary i i Bit i is 0 0 0 or 1 1 1. The implementation method is to shift the binary to the right i i i-bit re & 1 \&1 &1
l o w b i t lowbit The lowbit operation returns the last binary number 1 1 1. The implementation method is x & − x x\&-x X & − x, that is, the original code and the upper complement of a number, and the complement is (~ x x x+1), i.e. take the inverse and add 1

Algorithm implementation:

Given a sequence with length n, please find the number of 1 in the binary representation of each number in the sequence

#include <iostream>
using namespace std;

int lowbit(int x)
{
    return x & -x;
}

int main()
{
    int n;
    cin >> n;
    
    while (n -- )
    {
        int x;
        cin >> x;
        
        int res = 0;
        while(x)
        {
            x -= lowbit(x);
            res ++;
        }
        
        cout << res << ' ';
    }
    
    return 0;
}

Discretization

Algorithm idea: discretization is actually mapping. If the range of values is large and we need few points, there will be points with large intervals. If we store them directly, we will waste a lot of space. Therefore, we map them to adjacent array elements to reduce space and computation.

u n i q u e unique unique function implementation:

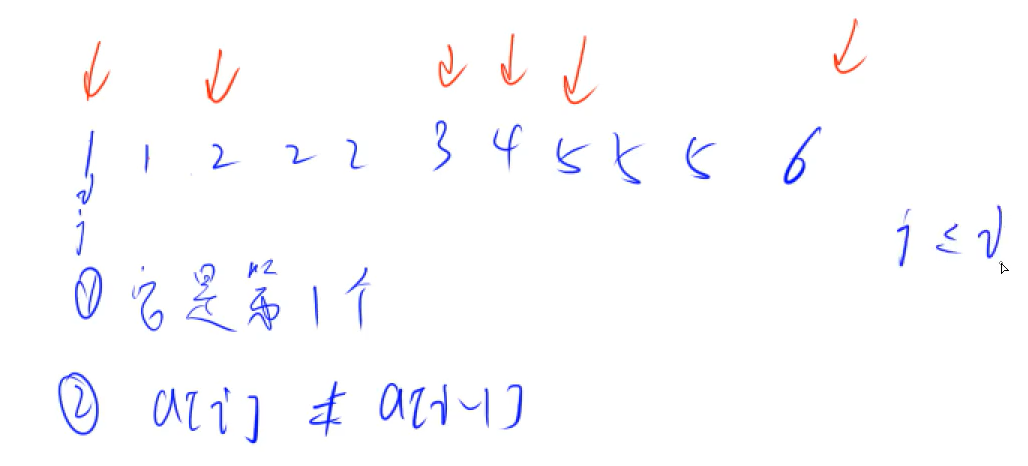
Algorithm implementation:

Suppose there is an infinite number axis, and the number on each coordinate on the number axis is 0. Now, let's start with n operations, each of which adds c to the number at a certain position x. Next, make m queries. Each query contains two integers L and r. you need to find the sum of all numbers between the interval [l,r].

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef pair<int, int> PII;
const int N = 300010;

int a[N],s[N];
vector<int> alls;
vector<PII> p, q;

//Coordinate mapping
int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    
    return l + 1; //Starting from 1, it is convenient to sum prefixes
}

// vector<int>::iterator unique(vector<int> &a)
// {
//     int j = 0;
//     for (int i = 0; i < a.size(); i ++ )
//         if (!i || a[i] != a[i - 1])
//             a[j ++ ] = a[i];
//     //a[0] ~ a[j - 1] non repeated numbers in all a

//     return a.begin() + j;
// }

int main()
{
    int n, m;
    cin >> n >> m;
    
    for(int i = 0; i < n; i++)
    {
        int x, c;
        cin >> x >> c;
        p.push_back({x,c});
        alls.push_back(x);
    }
    
    for(int i = 0; i < m; i ++)
    {
        int l, r;
        cin >> l >> r;
        q.push_back({l,r});
        alls.push_back(l);
        alls.push_back(r);
    }
    
    //duplicate removal
    sort(alls.begin(),alls.end());
    alls.erase(unique(alls.begin(),alls.end()), alls.end());
    
    //Changes after mapping
    for(int i = 0; i < p.size(); i ++)
    {
        a[find(p[i].first)] += p[i].second;
    }
    
    //Prefix Sum 
    for(int i = 1; i <= alls.size(); i ++) s[i] = s[i - 1] + a[i];
    
    //Output query results
    for(int i = 0; i < q.size(); i ++)
    {
        cout << s[find(q[i].second)] - s[find(q[i].first) - 1] << endl;
    }
    
    return 0;
    
}

Interval merging

Algorithm idea: interval merging is to merge the intersecting intervals into one interval

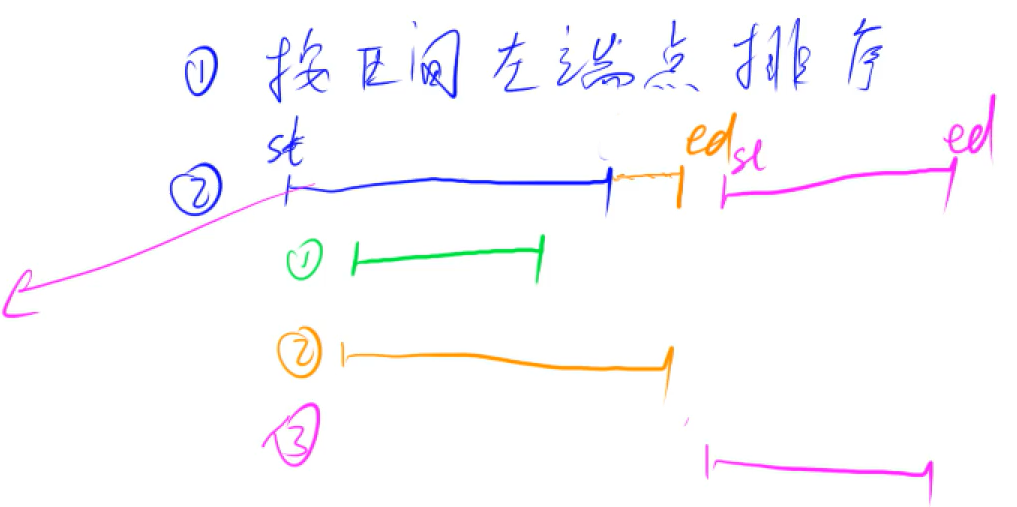
Algorithm implementation:

Given n intervals, it is required to merge all intersecting intervals. Note that if you intersect at the endpoint, there is also an intersection. Output the number of intervals after merging. For example: [1,3] and [2,6] can be combined into one interval [1,6].

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int N = 100010;

typedef pair<int, int> PII;

vector<PII> segs;

void merge(vector<PII> &segs)
{
    vector<PII> res;
    
    int l = -2e9, r = -2e9;
    for(auto seg : segs)
    {
        if(seg.first > r)
        {
            if(r != -2e9) res.push_back({l, r});
            l = seg.first;
            r = seg.second;
        }
        else r = max(r, seg.second);
    }
    
    if(l != -2e9) res.push_back({l,r});
    
    segs = res;
    
    return;
}
int main()
{
    int n;
    cin >> n;
    
    while (n -- )
    {
        int l, r;
        cin >> l >> r;
        segs.push_back({l,r});
    }
    
    sort(segs.begin(), segs.end());
    
    merge(segs);
    
    cout << segs.size() << endl;
    
    return 0;
}

High precision addition

Algorithm idea: calculate from low to high in turn to judge whether to carry
Algorithm implementation:

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

const int N = 100010;

vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    int t = 0;
    for(int i = 0; i < A.size() || i < B.size(); i ++)
    {
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if(t) C.push_back(t);
    return C;
}

int main()
{
    string a,b;
    cin >> a >> b;
    
    vector<int> A, B;
    for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');
    
    auto C = add(A, B);
    
    for(int i = C.size() - 1; i >= 0; i --) cout << C[i];
    cout << endl;
    
    return 0;
}

High precision subtraction

Algorithm idea: subtract from low to high to judge whether borrowing is required
Algorithm implementation:

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

bool cmp(vector<int> A, vector<int> B)
{
    if(A.size() != B.size()) return A.size() > B.size();
    else
    {
        for(int i = A.size() - 1; i >= 0; i --)
        {
            if(A[i] != B[i]) return A[i] > B[i];
        }
    }
    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    
    int t = 0;
    for(int i = 0; i < A.size(); i ++)
    {
        t = A[i] - t;
        if(i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if(t < 0) t = 1;
        else t = 0;
    }
    
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}
int main()
{
    string a, b;
    cin >> a >> b;
    
    vector<int> A, B;
    for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');
    
    if(cmp(A,B))
    {
        auto C = sub(A, B);
        for(int i = C.size() - 1; i >= 0; i --) cout << C[i];
    }
    else
    {
        cout << '-';
        auto C = sub(B, A);
        for(int i = C.size() - 1; i >= 0; i--) cout << C[i];
    }
    
    return 0;
}

High precision multiplication

Algorithm idea: multiply each high-precision bit by a smaller number, and then carry forward
Algorithm implementation:

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

vector<int> mul(vector<int> &A, int &b)
{
    vector<int> C;
    
    int t = 0;
    for(int i = 0; i < A.size() || t; i ++)
    {
        t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
     
    // while(t) 
    // {
    //     C.push_back(t % 10);
    //     t /= 10;
    // }
    
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    
    return C;
}
int main()
{
    string a;
    cin >> a;
    
    vector<int> A;
    for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
    
    int b;
    cin >> b;
    
    auto C = mul(A, b);
    
    for(int i = C.size() - 1; i >= 0; i --) cout << C[i];
    
    return 0;
}

High precision Division

Algorithm idea: start from the high bit, divide each bit by the smaller number, and take the remainder each time ∗ 10 *10 * 10 plus next
Algorithm implementation:

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;

vector<int> div(vector<int> &A, int &b, int &r)
{
    vector<int> C;
    
    r = 0;
    for(int i = 0; i < A.size(); i ++)
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    
    reverse(C.begin(), C.end());   //Easy to remove leading zeros
    while(C.size() > 1 && C.back() == 0) C.pop_back();
    
    return C;
}

int main()
{
    string a;
    cin >> a;
    
    vector<int> A;
    for(int i = 0; i < a.size(); i ++) A.push_back(a[i] - '0');
    
    int b;
    cin >> b;
    
    int r;
    auto C = div(A, b, r);
    
    for(int i = C.size() - 1; i >= 0; i --) cout << C[i];
    cout << endl << r;
    
    return 0;
}