• Data structure of undirected graph
  • Adjacency table array
• Depth first search
  • Depth first search for path
  • Performance characteristics of depth first search
• Breadth first search
• Comparison of two search methods

The graph shows the abstract model represented by the connected nodes. This model can be used to study such things as "whether to reach the specified point from one point", "how many nodes are connected to the specified node", "which is the shortest connection between two nodes". The algorithm of graph is related to many practical problems. For example, maps, search engines, circuits, task scheduling, business transactions, computer networks, social networks, etc.
Undirected graph is the simplest and most basic graph model, which consists of only a group of vertices and a group of edges that can connect two vertices.
In the implementation of graph, the nodes of graph are represented by integer value starting from 0, and the edges connecting nodes 8 and 5 are represented by 8-5. In undirected graph, the same edge is represented by 5-8. 4-6-3-9 represents a path between 4 and 9.

Data structure of undirected graph

The API of undirected graph

 public class Graph{
    Graph(int V)   //Create a graph with V vertices but no edges
    Graph(In in)   //Read in a picture from standard input stream in
    int v()     //Vertex number
    int E()    //Edge number
    void addEdge(int v， int w)    //Add an edge v-w to the graph
    Iterable<Integer>adj(intv)     //And all adjacent vertices
    String toString()      //String representation of object     
 }

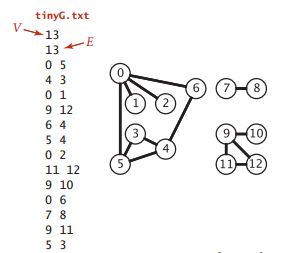
The input accepted by the second constructor consists of 2*E+2 integers. The first two lines are V and E respectively, indicating the number of vertices and edges in the graph. Next, each row is a pair of connected vertices.

Adjacency table array

The adjacency table array can be selected as the data structure to implement Graph. It stores all adjacent vertices of each vertex in a linked list. The adjacency table array constructed after reading tingG is as shown in the figure:

Code implementation:

public class Graph {
    private final int V; // vertex
    private int E; // edge
    private Bag<Integer>[] adj;

    public Graph(int V) {
        this.V = V;
        this.E = 0;
        adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v < V; v++) {
            adj[v] = new Bag<Integer>();
        }
    }

    public Graph(In in) {
        this(in.readInt());
        int E = in.readInt();
        for (int i = 0; i < E; i++) {
            int v = in.readInt();
            int w = in.readInt();
            addEdge(v, w);
        }
    }

    public int V() {
        return V;
    }

    public int E() {
        return E;
    }

    public void addEdge(int v, int w) {
        adj[v].add(w);
        adj[w].add(v);
        E++;
    }

    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

Using the array adj [] to represent the vertices of a graph can quickly access the list of adjacency vertices of a given vertex; using the Bag data type to store all adjacency vertices of a vertex can ensure to add new edges or traverse adjacency vertices of any vertex in a constant time. When you want to add such an edge as 5-8, the addEdge method will not only add 8 to the adjacency table of 5, but also add 5 to the adjacency table of 8.

The performance characteristics of this implementation are as follows:

• The space used is proportional to V+E
• The time required to add an edge is constant
• The time needed to traverse a vertex's adjacent vertices is directly proportional to the degree of the vertex (the degree of the vertex represents the number of edges connected to the vertex)

Depth first search

Depth first search is a way of traversing a graph. The trajectory of this algorithm is very similar to the maze. Maze can be regarded as graph, maze channel as graph edge, maze intersection as graph point, maze can be regarded as an intuitive graph. One way to explore the maze is called Tremaux search. The specific method of this method is to select an unmarked channel and lay a rope on the road; mark all the first crossing and channels; when arriving at the first marked crossing, go back to the previous crossing; when there is no available channel at the back crossing, continue to go back.
In this way, we can finally find a way out, and will not pass the same passage or intersection many times.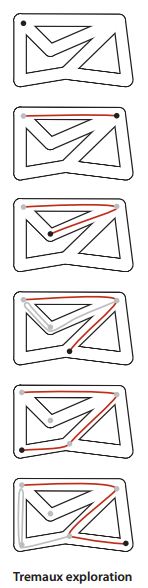

The code implementation of depth first search is similar to maze walking:

public class DepthFirstSearch {
    private boolean[] marked;
    private int count;
    private final int s;

    public DepthFirstSearch(Graph G, int s) {
        marked = new boolean[G.V()];
        this.s = s;
        dfs(G, s);
    }

    private void dfs(Graph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G, w);
            }
        }
    }

    public boolean marked(int w) {
        return marked[w];
    }

    public int count() {
        return count;
    }
}

This code will search out all the points adjacent to the vertex s, the recursive call mechanism of dfs() method in and the function of the marked array corresponding to the rope in the maze. When all the adjacent vertices of a vertex have been processed, the recursion will end. When the algorithm is running, it will always go deep along the first adjacent vertex of a vertex, until it meets a vertex that has been marked in the marked array, it exits recursion layer by layer, which is also the origin of depth first search name. The final search results are stored in the marked array, and the index corresponding to the bit marked as true is the point connected to the vertex s.

Depth first search for path

Depth first search can solve the problem of path detection, that is to say, "is there a path between two given vertices?" , but what if you want to find this path? To answer this question, just extend the above code slightly:

public class DepthFirstPaths {
    private boolean[] marked;
    private int[] edgeTo;  //New for recording paths
    private final int s;

    public DepthFirstPaths(Graph G, int s) {
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];  
        this.s = s;
        dfs(G, s);
    }

    private void dfs(Graph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                edgeTo[w] = v;  //Record path
                dfs(G, w);
            }
        }
    }

    public boolean marked(int w) {
        return marked[w];
    }

    public int count() {
        return count;
    }

    public boolean hasPathTo(int v) {   //Determine if there is a path from s to v
        return marked(v);
    }

    public Iterable<Integer> pathTo(int v) {  //Get the path from s to v, and return null if it does not exist
        if (!hasPathTo(v))
            return null;

        Stack<Integer> path = new Stack<Integer>();
        for (int x = v; x != s; x = edgeTo[x]) {
            path.push(x);
        }

        path.push(s);
        return path;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        Graph G = new Graph(in);
        int s = Integer.parseInt(args[1]);
        DepthFirstPaths search = new DepthFirstPaths(G, s);

        //
        for (int v = 0; v < G.V(); v++) {
            StdOut.print(s+" to "+v+": ");
            if(search.hasPathTo(v)){
                for(int x:search.pathTo(v)){
                    if(x==s) StdOut.print(x);
                    else StdOut.print("-"+x);
                }
            }
            StdOut.println();
        }
    }
}

This code adds edgeTo [] shape array to play the role of rope in Tremaux search. Every time edge v-w accesses w for the first time, edgeTo[w] is set to v. finally, edgeTo array is a tree with the starting point as the root node, recording the path from any connected node to the root node.
The following figure is an example of the content of edgeTo generated by a pair of graphs and the structure of the path tree: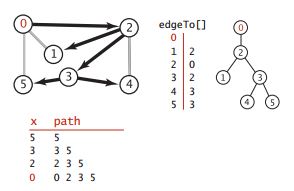

This is consistent with the code running result:

java DepthFirstPaths tinyCG.txt 0
0 to 0: 0
0 to 1: 0-2-1
0 to 2: 0-2
0 to 3: 0-2-3
0 to 4: 0-2-3-4
0 to 5: 0-2-3-5

Performance characteristics of depth first search

The time required for depth first searching all vertices connected with the starting point is directly proportional to the sum of degrees of vertices.
Using depth first search, the time needed to get the path from a given starting point to any marked vertex is directly proportional to the length of the path.

Breadth first search

The path obtained by depth first search is not only related to the structure of the graph, but also affected by the representation of the graph. The order of the vertices in the adjacency table is different, and the path obtained will be different. So when we need to calculate the shortest path between two points (single point shortest path), we can't rely on depth first search, and breadth first search can solve the problem of single point shortest path.
To find the shortest path from s to V, starting from s, find v in all the vertices that can be reached by one edge, if not, continue to find v in the vertices that are s away from two sides, and so on.

public class BreadthFirstPaths {
    private boolean[] marked;
    private int[] edgeTo;
    private final int s;

    public BreadthFirstPaths(Graph G, int s) {
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        this.s = s;
        bfs(G, s);
    }

    private void bfs(Graph G, int s) {
        Queue<Integer> queue = new Queue<Integer>();
        marked[s] = true;
        queue.enqueue(s);
        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            for (int w : G.adj(v)) {
                if(!marked[w]){
                    edgeTo[w]=v;
                    marked[w]=true;
                    queue.enqueue(w);
                }
            }
        }
    }

    public boolean hasPathTo(int v){
        return marked[v];
    }

    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v))
            return null;

        Stack<Integer> path = new Stack<Integer>();
        for (int a = v; a != s; a = edgeTo[a]) {
            path.push(a);
        }

        path.push(s);
        return path;
    }

    
     // cmd /c --% java algs4.four.BreadthFirstPaths ..\..\..\algs4-data\tinyCG.txt 0
     public static void main(String[] args) {
        In in = new In(args[0]);
        int s = Integer.parseInt(args[1]);
        Graph g = new Graph(in);
        BreadthFirstPaths search = new BreadthFirstPaths(g, s);

        for (int i = 0; i < g.V(); i++) {
            StdOut.print(i + ":");
            Iterable<Integer> path = search.pathTo(i);
            for (Integer p : path) {
                if (search.s != p) {
                    StdOut.print("-" + p);
                } else {
                    StdOut.print(p);
                }
            }
            StdOut.println();
        }
    }
}

Method bfs defines a queue to hold all vertices that have been marked but whose adjacency table has not been checked. First add the starting point to the queue, and then repeat the following steps until the queue is empty:

• Take the next vertex v in the queue and mark it
• All unmarked vertices adjacent to v are queued.
  The first in first out (FIFO) feature of queue can achieve the effect of increasing the search distance of breadth first search. In depth first search, a stack following LIFO rule is used implicitly. In the recursive call of dfs, the stack is managed by the system.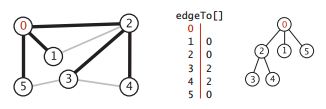
  

Comparison of two search methods

Both depth first and breadth first search algorithms store the starting point in the data structure, and then repeat the following steps until the data structure is cleared:

• Take the next vertex v and mark it
• Adding unmarked vertices adjacent to v to the data structure
  The difference between the two algorithms lies in the rules of getting the next vertex from the data structure. The depth first search will first take the vertex that is the latest to join the data structure, while the breadth first search will take the vertex that is the first to join. The difference of this rule will affect the path of the search graph, depth first search will continue to go deep into the graph, and all the forked vertices will be saved in the stack, while breadth first search will scan the graph like a fan, and use a queue to save the most visited vertices of the first segment.