The so-called greedy algorithm is to ensure that each operation is a local optimal solution, so that the final result is a global optimal solution.

Exercise 1:455. Distribute cookies

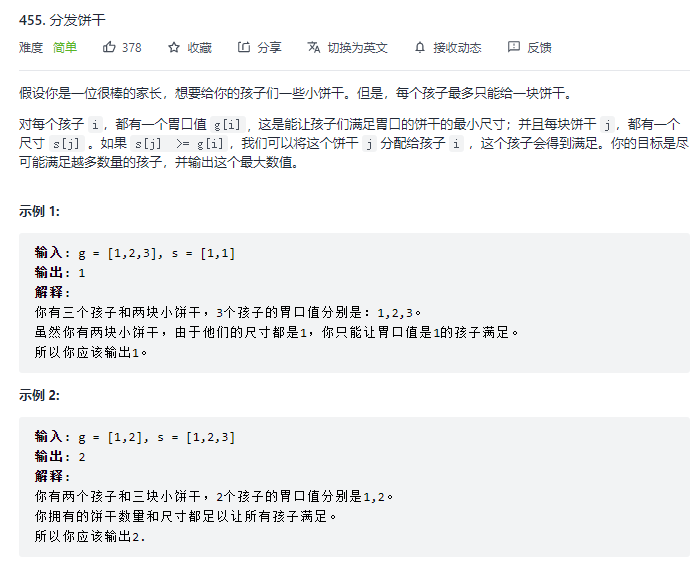
The key to using greedy algorithm is to find greedy strategy, that is, each operation is a local optimal solution.

As can be seen from the question, to satisfy as many children as possible, as long as the child with the smallest appetite is allocated the smallest size of biscuits that can satisfy him, this is the greedy strategy of this question.

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        if(g.size()==0||s.size()==0) return 0;  //Consider special circumstances

        sort(g.begin(),g.end());  //Sort in ascending order
        sort(s.begin(),s.end());

        int cnt=0;
        int j=0;
        for(int i=0;i<g.size();){
            if(s[j]>=g[i]){
                //If the biscuit size is greater than or equal to the appetite value
                ++i;
                ++cnt;
            }
            ++j;
            if(j==s.size()) break;
        }

        return cnt;
    }
};

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());  //Sort in ascending order
        sort(s.begin(),s.end());

        int child=0,cookie=0;
        while(child<g.size()&&cookie<s.size()){
            if(g[child]<=s[cookie])++child;
            ++cookie;
        }
        return child;
    }
};

135 distribute candy

We can split this sentence into two rules: the children with high scores must get more candy among the adjacent children.
Left rule: when ratings [i-1] < ratings [i], student I will have more candy than child i-1.
Right rule: when rating [i] > rating [i+1], student I will have more candy than student i+1.

Problem solving ideas:
1. Walk from left to right and record the minimum number of candy required at the current point;
2. Walk from right to left and record the minimum number of candy required at the current point;
3 take the maximum value of each point, and the sum is the result.

class Solution {
public:
    int candy(vector<int>& ratings) {
        int n=ratings.size();
        vector<int>vec(n,0);
        int left=0;
        for(int i=0;i<n;++i){
            if(i>0&&ratings[i]>ratings[i-1]){
                vec[i]=++left;
            }
            else{
                left=1;
                vec[i]=left;
            }
        }

        int right=0,ret=0;
        for(int i=n-1;i>=0;--i){
            if(i<n-1&&ratings[i]>ratings[i+1]){
                ++right;
            }else{
                right=1;
            }
            ret+=max(right,vec[i]);
        }
        return ret;
    }
};

452. Detonate the balloon with the least number of arrows

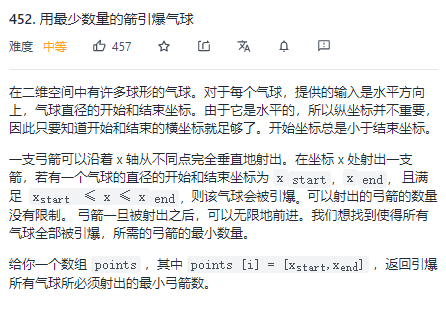
**Greedy strategy: * * first arrange all balloons and the right boundary in ascending order, so you can shoot the smallest balloon on the right boundary every time. The balloon on the right side of the left boundary in front of the right boundary will not explode, and the others have exploded. Then select the smallest balloon on the right boundary among the balloons that have not exploded. By analogy, it is the optimal solution to solve this problem.

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        int n=points.size();
        //Arrange from small to large according to the right boundary
        sort(points.begin(),points.end(),
        [](const vector<int>&a,const vector<int>& b){
            return a[1]<b[1];
        });

        int cnt=1;
        int prev=points[0][1];
        for(int i=1;i<n;++i){
            if(points[i][0]>prev){
                ++cnt;
                prev=points[i][1];
            }
        }

        return cnt;
    }
};

763. Division of letter interval

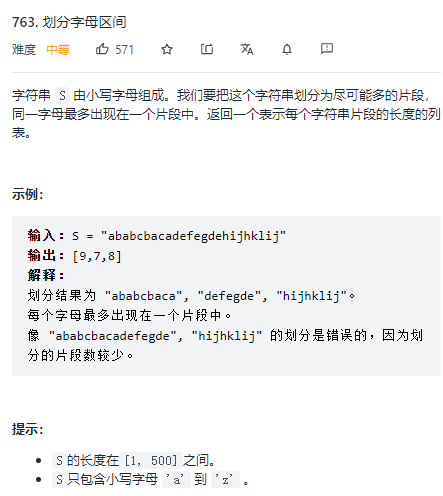
dynamic programming

greedy strategy

Record the first occurrence time and the last occurrence time end of all characters;
Sort by left boundary from small to large;
Left record the left boundary of the current segment;
pos records the right boundary of the current segment;

Left is set as the left bound of the first interval, which must be 0;
pos is set as the right bound of the first interval;
Enter the cycle, starting from the next interval of the first interval;
If the left bound of the next interval is less than pos, it means that it should be divided into a segment. Therefore, update pos to the larger value of the current pos and this interval;
If the right bound of the next interval is greater than pos, it means that [left,pos] is a segment and the segment length is recorded; Update left to the left bound of the current interval and pos to the right bound of the current interval.

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int n = s.size();
        vector<vector<int>>position(26,vector<int>(2,-1));

        unordered_map<char, int>ch_cnt;
        //position records the subscript of the first and last occurrence of a character
        for (int i = 0;i < n;++i) {
            if (ch_cnt[s[i]] == 0)
                position[s[i] - 'a'][0] = i;
            position[s[i] - 'a'][1] = i;
            ++ch_cnt[s[i]];
        }

        //Sort: sort the interval of each character from small to large according to the left boundary
        sort(position.begin(), position.end(),
            [](const vector<int>& a, const vector<int>& b) {
                return a[0] < b[0];
            });

        //It doesn't matter
        int i = 0;
        while (i < 26 && position[i][0] == -1)
            ++i;

        vector<int>ret;  //Storage results
        int left = 0;
        int pos = position[i][1]; //Record right bound
        for (i = i + 1;i < 26;++i) {
            if (i == 25) {
                if(position[i][0]>pos){
                    ret.push_back(pos - left + 1);
                    ret.push_back(position[i][1]-position[i][0]+1);
                    break;
                }else{
                    pos = max(position[i][1], pos);
                    ret.push_back(pos-left+1);
                }  
            }
            if (position[i][0] < pos) {
                //If there are overlapping parts
                //Update the pos and select a larger one
                pos = max(position[i][1], pos);
            }
            else {
                //No coincident parts
                ret.push_back(pos - left + 1);
                left = position[i][0];
                pos = position[i][1];
            }
        }
        return ret;
    }
};