1, Algorithm
++n
n + + differences
int n=1,n1,n2;
n1=++n;
System.out.println(n1);
System.out.println(n);
n2=n++;
System.out.println(n2);
System.out.println(n);
2
2
2
3
1. Concept
Philosophy of writing algorithms:
From simple to complex: verify step by step and print more intermediate results
Part first and then whole: subdivide when there is no idea
Rough first and then fine: variable renaming, statement merging and boundary processing (length-1 and length-2) are all tried. You can write a non tangled and refined method first
Philosophy of de bug ging:
Step 1: read through the program to make sure you understand the logic of the whole program and you can't read the bug
Step 2: if there is still a bug, output the intermediate value
Step 3: if there are still bug s, reduce the functions and leave the core
In the worst case, you can't do it just by looking at it
algorithm: Algorithms for different solutions to the same problem are often specific to specific data structures
Data Structure: different ways of storing data in Data Structure: a tube of apples (there is no gap in the middle of the array, data cannot be inserted into the linked list, and data can be inserted) a basket of apples
The search is much faster than the linked list for the array. The linked list should look down the chain one by one
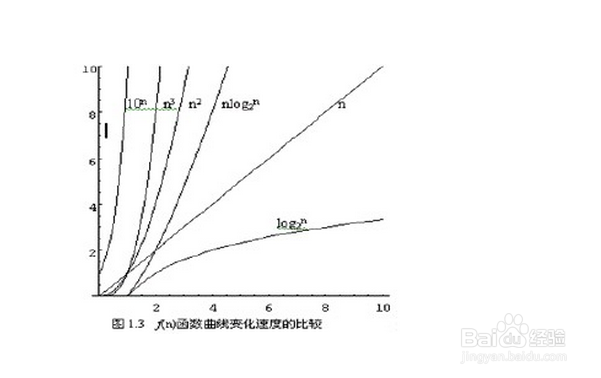
Big O: academic time representation to determine the quality of the algorithm
Time measurement: the shorter the time, the better. The time is calculated by the time difference (System.currentTimeMillis() prints out the start time and end time respectively). However, for some not very complex algorithms, the time difference may be rounded to 1s. This time can put the algorithm in the cycle and increase the time, that is, the amplitude is not enough to round up
Space calculation: counting the apples in the basket needs the help of another basket, which takes up other space. The less space, the better the algorithm
Time complexity: the complexity of time is the change law of time with the expansion of the problem scale
O (ignoring the higher-order term of the coefficient)
The sample is large enough, and those are not very important, so they can be ignored
Represents the worst time complexity
There are average and best, these interviews are not tested
Spatial complexity: with the expansion of the scale of the problem, the change law of space is to see the additional space rather than the allocation of spatial variables necessary for the problem. Those local variables that must be allocated are not included in the spatial complexity

Operation not to be considered: program initialization with initial value
Ignore: O(2n) and O(n) are almost the same. Ignoring 2 O(n^2+2n) is also directly ignoring 2n
eg1. For an array with a size of 10 and an array with a size of 10000, there is no difference in accessing the last element of the array
That is, with the expansion of the scale of the problem, the time basically does not change, expressed as O(1), a constant
eg2. For accessing a certain location in the linked list (if it is all location 1, it must be O(1), but we generally say that the time complexity is the worst case), so it is assumed that the value scale of the last location in the linked list is 10 1s and the scale is 100 10s O(n) linear change
The most common are O(1) and O(n). If the last position of the access linked list is cycled twice, it is O(n2), and the third cycle is O(n3)
eg2: time complexity of averaging an array
O(n) because you want to add up all the numbers of the array
2. sort
Sorting is to arrange a group of numbers without order from small to large or from large to small
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-t1XPpyBk-1638342991072)(C:\Users \ Mississippi watch \ appdata \ roaming \ typora \ typora user images \ image-20210308114914739. PNG)]
The four most important types are: inserting, stacking, merging and fast sorting
Selective bubble insertion
Quick return to the Greek statistical base
EN Fang, en Lao, en 13
Yes, Enga k, Enga times k
Unstable, unstable, unstable
Unstable unstable stable
2.1 select sort
The so-called selective sorting is to continuously select the smallest (largest)
The simplest and most useless (time complexity is too high O(n^2) and unstable) sorting algorithm has a certain optimization space
By comparing the subscript that continuously determines the minimum value, this subscript is constantly changing. Traverse the subscript that determines the minimum value and exchange the value at the first position. The second traverse starts from the second number, then exchanges with the second value, and so on.
1. Treatment process
package com.liu.algorithm.sort;
public class SelectionSort {
public static void main(String[] args) {
int[] arr={4,3,5,1,9,6,7,2,8};
//Optimization 1: handle the boundary value, change arr.length to arr.length-1, and the outer cycle will be less than once
for (int i=0;i<arr.length-1;i++){
int minPostion=i;
for (int j=i+1;j<arr.length;j++){
//Optimization 2: statement merging
// if (arr[j]<arr[minPostion]){
// minPostion=j;
// }
minPostion=arr[j]<arr[minPostion]?j:minPostion;
}
// System.out.println("the subscript of the minimum value is:" + minpostion ");
//Optimization 5: two position exchange refining method
swap(arr,i,minPostion);
//Optimization 3: print the sorting results after each cycle
System.out.println("This is the second"+i+"After one loop, the contents of the array");
print(arr);
//Optimization 4: repeated code writing method
// for (int k =0;k<arr.length;k++){
// System.out.print(arr[k]+" ");
// }
System.out.println();
}
System.out.println("The final result is:");
print(arr);
// for (int i=0;i<arr.length;i++){
// System.out.print(arr[i]+" ");
// }
// for (int arrays:arr){
// System.out.print(arrays+" ");
// }
}
static void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
static void print(int[] arr){
for (int i=0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
}
}
/*
Step 1: define an array (array initialization)
Step 2: print out the array
Step 3: print out the subscript of the smallest group of elements (compare the first element with the remaining elements one by one, and constantly refresh the defined subscript value)
Step 4: exchange the position between the smallest element and the first element. At this time, the first element is arranged
Step 5: repeat the above process and compare the remaining elements, that is, put a for loop on the outermost layer
Step 6: Optimization: the code for exchanging and printing arrays is abstracted into methods, and the outermost boundary value of ternary operators prints out the results of each cycle
Step 7: explore deep optimization, that is, you can find the minimum and maximum values at the same time, put them at both ends, or compare the first element with the second and third elements at the same time
*/
2. Complete code
package com.liu.algorithm.sort;
public class SelectionSort_1 {
public static void main(String[] args) {
int[] arr = {31, 33, 38, 22, 45, 16, 90, 35, 90};
for (int i = 0; i < arr.length - 1; i++) {
int minPostion = i;
for (int j = i + 1; j < arr.length; j++) {
minPostion = arr[j] < arr[minPostion] ? j : minPostion;
}
swap(arr, i, minPostion);
System.out.println("This is the second" + (i + 1) + "Results after cycle");
print(arr);
System.out.println();
}
System.out.println("======This is the final result======");
print(arr);
}
static void swap(int[] arr, int i, int j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
static void print(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
(1) bigO analysis
Find the one that consumes the most time for analysis. You don't need to analyze all of them. If there are two for loops, it depends on the execution time of the statement in the middle of the two for loops
The best and worst are O(n^2). The so-called best is that it has been sorted, but it still needs to traverse all the numbers in the array
Space complexity O(1) indicates that no additional space is occupied
Instability is that two equal numbers are sorted, and their relative order may change after sorting
How to prove that the selection sorting is unstable:
5 6 5 2 1 the order of the second 5 will be in front of the first 5
Consequences of instability: if Xiao Wang and Lao Wang, who are also bank customers, are of the same age, but the bank's deposits and membership levels are different, if the order is reversed, some business logic of the bank may be disrupted. For example, in the case of the same age, people with high membership levels can handle well, resulting in logical contradictions.
(2) Verification algorithm - logarithm
Logarithm: compare what you write with what the system writes (Arrays.sort(arr);) and the output result is a logarithm
How to verify the correctness of the algorithm?
- Visual observation (the test program can be used for real engineering calculation, and it is impossible to cite all cases)
- Generate enough random samples
- Calculate the sample results with the correct algorithm
- Verify with your own algorithm and compare the verification results
2.2 bubble sorting
Bubbling is to compare the smallest or largest number to the last
Spatial complexity: O(1) does not involve any additional space
Time complexity: O(n^2)
Stability: the stable pairwise comparison is not the jumping comparison like the selective sorting, but may jump to the back
Optimize bubble sorting: the best time complexity is O(1)
2.3 insert sort (*)
It is better to use insert sort for basically ordered arrays, which is twice as fast as bubble sort and faster than selection sort
stable
Time complexity:
O(n^2) (6 5 4 3 2 1) compare n+n-1+n-2 + 1 arithmetic sequence
It is better to compare O(n) and find that there is no need to exchange without moving (1 2 3 4 5)
Compare once
Space complexity: O(1)
Insertion sorting is to compare the second element to the last element, and insert and move slowly
It's kind of like the bubble sort ahead
2.4 summary selection bubble insertion
Play the game called Fighting the Landlord
The space complexity of bubble selection and insertion is O(1) and the time complexity is O(n^2). The last two are O(n)
Bubbling: basically no pairwise comparison, pairwise exchange is too slow
Choice: basically not unstable
Insertion: the efficiency is high when the sample is small and basically orderly
2.5 Hill sorting
I don't use too much, and I don't use too much for the interview
Improved insertion Sort Hill sort is a special insertion sort with interval > = 1. The interval of ordinary insertion sort is 1
When the interval is large, the number of moves is relatively small, the moving distance is relatively long, and the jumping row is unstable
Take out a number every other interval to form a new array
The optimization of hill sorting is mainly reflected in the interval sequence
At first, it takes half the length of the array as the interval sequence, and then half, half and so on
Knuth sequence
H = 3 * H + 1 h = 1, 1, 4, 7, 10, 13, H max. < = 1 / 3 of the entire array length
Time complexity: best O(n^1.3)
Space complexity: O(1)
Stability:
2.6 merge sort (*)
2.6.1 recursion
A method calls itself in its internal execution process. Dogs bite their own tail. Strictly speaking, they are not the same method, because the parameters are different.
Recursion requires a stop condition, that is, Base case
package com.liu.algorithm.sort;
public class Recursion {
public static void main(String[] args) {
System.out.println(f(10));
}
static long f(int n){
//Without these two conditions, stack overflow will occur
if (n<1){
return -1;
}
if (n==1){
return 1;
}
return n+f(n-1);
}
}
Operation result: 5
merge sort
Special for Java object sorting (TIM SORT improved merge sorting)
Continue to divide into half, divide until it can't be divided again (that is, there are only two numbers or one number in the array), and then merge (the premise of merging is that the two arrays have been arranged in order)
Time complexity: because it is constantly divided into two, logarithmic function
Space complexity:
Stability:
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-l7rhskk3-163834991079) (C: \ users \ Mississippi watch \ appdata \ roaming \ typora \ typora user images \ image-20210311165546356. PNG)]
java object sorting
- Object sorting generally requires more stable object attributes
2.7 quick sort (*)
Single shaft fast exhaust
Double axis fast exhaust
Now there is an array with the last number as the reference. Those less than it are placed on the left and those greater than it are placed on the right. Of course, both the left and right are to the left of the last number
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-uWkTPohX-1638342991083)(C:\Users \ Mississippi watch \ appdata \ roaming \ typora \ typora user images \ image-20210311183813803. PNG)]
java internal Array double axis fast sorting, which is an improved algorithm for fast sorting
Arrays.sort(arr);
2.8 counting and sorting
Non comparative sorting is suitable for some special cases
A kind of bucket thought
Algorithm idea: large quantity and small range
- The age of tens of thousands of employees in a large company is 18-80
- College entrance examination score 0-750
The number of occurrences of each number is taken as the element value of the new array, and the size of the value is taken as the subscript value of the new array, and then these numbers are re formed into a new array from small to large
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-yCLBv4OP-1638342991085)(C:\Users \ Mississippi watch \ appdata \ roaming \ typora \ typora user images \ image-20210312123125951. PNG)]
Result array: 001222223334455566667777899
Space complexity: n+k(k buckets)
Time complexity: n+k (n)
2.9 cardinality sorting
Non comparison sort
A kind of bucket thought
Multi keyword sorting
The first place is ten and the first place is hundred
Space complexity: O(n)
Time complexity: O(n)
Stable sorting
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-gDocPa6Q-1638342991088)(C:\Users \ Mississippi watch \ appdata \ roaming \ typora \ typora user images \ image-20210312205357148. PNG)]
2.10 bucket sorting
Maximum value - minimum value = difference is divided into buckets according to the difference. One bucket represents a range, and each bucket is sorted separately
unimportance
3. Binary sorting
Find whether a number exists in an ordered array
Keep cutting in half
How many times
Look at 2 ^ (several times) = array length
Several times = log2 array length
The complexity is (log2 array length) = log2n
This means that the log is based on 2
logn is based on 2 by default in the computer
Disordered dichotomy
4. XOR
exclusive OR is abbreviated as xor or eor
The difference is 1. The symbol is ^ no carry addition
0^N== N
N^N===0
XOR satisfies commutative law and associative law (the result of the same number XOR must be the same)
The same position only depends on the even number or odd number of 1, which has nothing to do with the order
Use of XOR
Title 1: int a=x;
int b=y;
Let the value of ab exchange
a=a^b
b=a^b
a=a^b
That's it
This is true if the values are the same, but not if the memory is the same
package com.liu.algorithm.erfen;
/**
* @author : Liu Ke
* @date : 2021-12-01 23:23
**/
public class Demo {
public static void main(String[] args) {
int[] arrs={1,2,3};
swap(arrs,0,0);
System.out.println(arrs[0]);
System.out.println(arrs[1]);
}
public static void swap(int[] arrs,int i,int j){
arrs[i]=arrs[i]^arrs[j];
System.out.println("arr[0]="+arrs[0]);
arrs[j]=arrs[i]^arrs[j];
System.out.println("arr[0]="+arrs[0]);
arrs[i]=arrs[i]^arrs[j];
}
}
Topic 2:
In an array, only one number is odd and the others are even
Find this number
Take all the numbers in the array out of XOR, and the most result is this number
The XOR result between even numbers is 0
The odd number is the last one
int xor=0;
int xor=xor^a[0]
int xor=xor^a[1]
.
.
int xor =xor^a[n]
Topic 3:
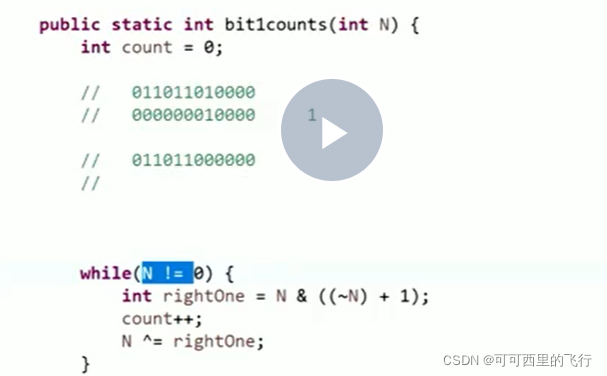
Binary number N,Take its rightmost 1
N&(Reverse N+1)
Topic 4:
Two numbers in a group appear odd times, and the other numbers appear even times. Find these two numbers
int xor=a^b!=0
therefore xor The first t Bit must be 1, so either a The first t Bit is 1, or b The first t Bit 1.(Find the confirmation with 1 on the far right t In fact, you don't have to find the position. The rightmost is 1. Any 1 is OK)
Divide the whole group into two groups. One group is the second group t Bit is 1, and one group is the second t Bit 0.
One of the XOR groups gets a or b,xor',Then another number is xor^xor'
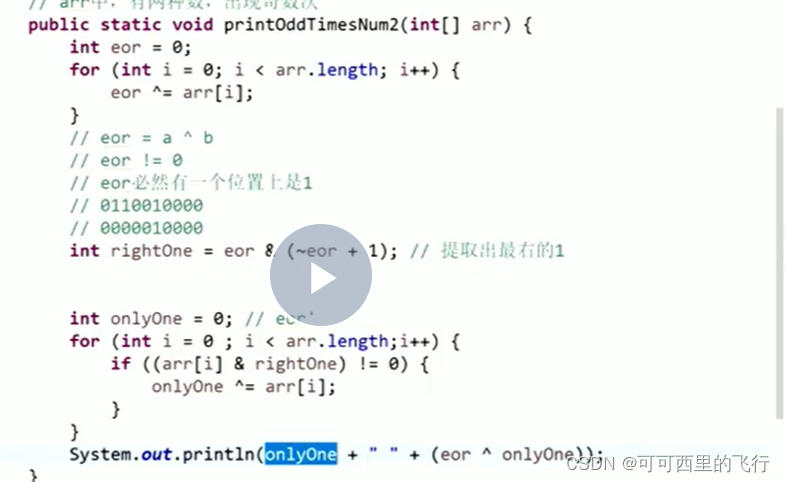
expand:
Find a number, how many 1
# 2, Data structure
Non comparative sorting is suitable for some special cases
A kind of bucket thought
Algorithm idea: large quantity and small range
- Age ranking of tens of thousands of employees in a large company 18-80
- College entrance examination score 0-750
The number of occurrences of each number is taken as the element value of the new array, and the size of the value is taken as the subscript value of the new array, and then these numbers are re formed into a new array from small to large
[External chain picture transfer...(img-yCLBv4OP-1638342991085)]
Result array: 001222223334455566667777899
Space complexity: n+k(k Barrels)
Time complexity: n+k(n)
## 2.9 cardinality sorting
Non comparison sort
A kind of bucket thought
Multi keyword sorting
The first place is ten and the first place is hundred
Space complexity: O(n)
Time complexity: O(n)
Stable sorting
[External chain picture transfer...(img-gDocPa6Q-1638342991088)]
## 2.10 bucket sorting
Maximum-minimum value=The difference is divided into buckets according to the difference. One bucket represents a range, and each bucket is sorted separately
unimportance