Catalog
5. Delete maximum element - delMax()
1, background
Consider the following: enter N int values to find the maximum (or minimum) M int values. This scenario can appear in: for example, there are a lot of records for each month's bill, I only need to consume the largest five records. So what is our implementation method?
Method 1: sort the N int values and output the largest M in turn. (if the amount of data is huge, you have to wait until the sorting is finished to get the value you want, not immediately.)
Method 2: every time a new consumption record is inserted, it is compared with the M (5) largest record. (unless m is small, it will cost a lot)
Method 3: priority queue (when inserting, the largest element has been placed in the appropriate position, waiting for getting)
2. Priority queue
Priority queue is an abstract data type, similar to stack and queue, but with different functions.
Its main functions are: 1. Delete (get) the largest element;
2. Insert element
There are three ways to insert and delete elements:
The first is to sort when inserting, so that you can take it directly. (ordered array)
The second is to get the largest element through traversal when inserting. (unordered array)
The third is the binary pile. Here are three kinds of time complexity.

3. Binary pile
Binary heap is a special kind of heap. Binary heap is a complete binary tree (binary tree) or a nearly complete binary tree (binary tree). There are two types of binary stacks: Maximum heap and Minimum heap . Maximum heap: Parent node The key value of is always greater than or equal to any child node The key value of the parent node is always less than or equal to the key value of any child node.
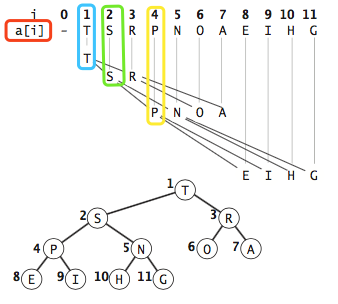
General use of binary reactor array To represent. If the position of the root node in the array is 1, the children of the nth position are 2n and 2n+1, respectively. Therefore, the children of the first position are at 2 and 3, and the children of the second position are at 4 and 5. and so on. This 1-based array storage method is convenient to find the parent and child nodes.
In the following figure, the child nodes of a[1] are a[2] and a[3]
4. Insert function - insert()
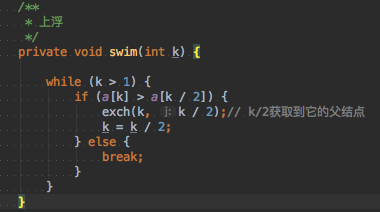
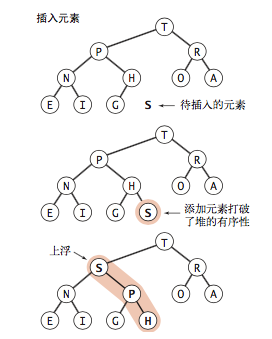
To insert an element, we will first place it at the end of the array, then find the subscript of its parent node according to k/2, and compare it with it. If it is larger than a[k/2], then replace the parent node. In this way, we can ensure that the root node a[1] (a[0] is not used) is always the largest element.
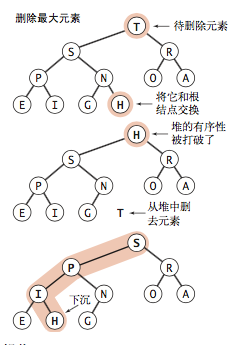
5. Delete maximum element - delMax()
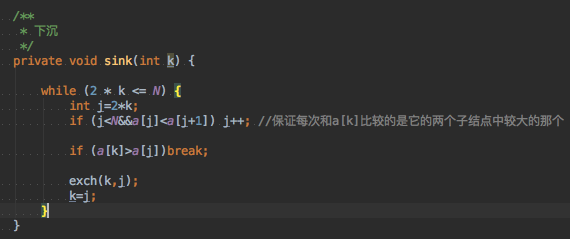
We remove the largest element from the top of the array and put the last element of the array at the top, reducing the size of the heap and letting this element sink into place.
6. Full code
public class MaxPQ {
private static double[] a;
private static int N = 0;
private MaxPQ(int lenght) {
a = new double[lenght + 1];
}
public void insert(double item) {
a[++N] = item;
swim(N);
}
/**
* Delete the largest element in the heap
*/
public double delMax() {
double maxItem = a[1];
a[1] = a[N--];// After you get the a[N] element, N will be minus one
a[N+1] = 0; // If this is an object, it can be used to empty and release the reference of the object to prevent the object from dissociating
sink(1);// Sink the new root node to the proper position and reorder the heap
return maxItem;
}
/**
* Go up
*/
private void swim(int k) {
while (k > 1) {
if (a[k] > a[k / 2]) {
exch(k, k / 2);// k/2 gets its parent
k = k / 2;
} else {
break;
}
}
}
/**
* Sink
*/
private void sink(int k) {
while (2 * k <= N) {
int j=2*k;
if (j<N&&a[j]<a[j+1]) j++; //The larger one of its two child nodes is guaranteed to be compared with a[k] every time
if (a[k]>a[j])break;
exch(k,j);
k=j;
}
}
private void exch(int i, int j) {
double temp = a[i];
a[i] = a[j];
a[j] = temp;
}
public static double[] getA() {
return a;
}
private static void show(double[] a) {
System.out.println("\n");
for (double item : a) {
System.out.print((int) item + ",");
}
}
public static void main(String[] args) {
double[] a = { 55, 43, 23, 12, 13, 11, 7, 8, 88, 6, 3, 2, 4, 1, 9, 8, 7, 11, 56, 45, 22, 23,
45, 66 };
MaxPQ maxPQ = new MaxPQ(a.length);
for (double item : a) {
maxPQ.insert(item);
}
show(getA());
for (int i=0;i<a.length;i++){
maxPQ.delMax();
show(getA());
}
}
}7. Trigeminal tree
The priority queue code above is implemented in the form of a complete binary tree. Can we use a trident tree or more trees to implement the priority queue?
The parent node of Trident tree is located at (k+1)/3, and the child node is located at 3k-1, 3k, 3k+1. The main code we changed is the floating and sinking code. The modified code is as follows: (according to the implementation of the following code, we can realize the form of multi fork tree, and we have to experiment ourselves if it is not good enough.)
/**
* Go up
*/
private void swim(int k) {
while (k > 1) {
if (a[k] > a[(k+1) / 3]) {
exch(k, (k+1) / 3);// k/2 gets its parent
k = (k+1) / 3;
} else {
break;
}
}
}
/**
* Sink
*/
private void sink(int k) {
int max;
while ( (3*k-1) <= N) {
int j=3*k-1;
max=j;
while (j<3*k+1&&j<N) {//The larger one of its two child nodes is guaranteed to be compared with a[k] every time
if (a[j] < a[j+1]) max=j+1;
j++;
}
if (a[k]>a[max])break;
exch(k,max);
k=max;
}
}

