Graph of akka-stream is an arithmetic scheme. It may represent a simple linear data flow graph such as Source/Flow/Sink, or it may be a composite flow graph composed of more basic flow graphs with relatively complex points, and the composite flow graph itself can be used as a component to compose a larger Graph. Because Graph is only a description of data stream operations, it can be reused. So we should try our best to design and build Graph according to business process needs. Implement Graph modular at a higher level of functionality. As discussed last time, Graph can be described as a black box whose entrance and exit are Shape, while the internal function of processing Gettage is described by Graph Stage. Below are some basic data flow diagrams of akka-stream presupposition:

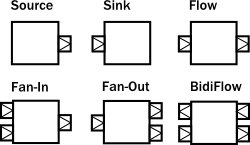
The Source, Sink and Flow above represent a flow chart with linear-stage steps, which belong to the most basic components and can be used to build data processing chains. Fan-In merge and Fan-Out diffusion have multiple input or output ports, which can be used to construct more complex data flow graphs. These basic Graph s can be used to construct more complex composite flow diagrams, which can be reused to construct more complex composite flow diagrams. Here are some common composite flow graphs:

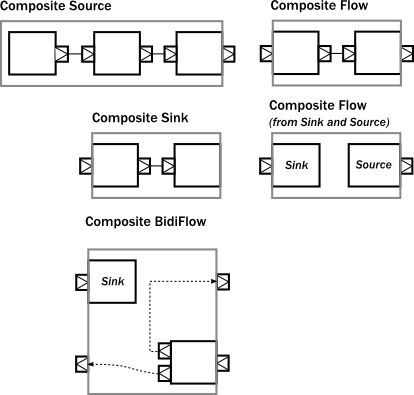
Note that the Composite Flow(from Sink and Source) above can be constructed using the Flow.fromSinkAndSource function:

def fromSinkAndSource[I, O](sink: Graph[SinkShape[I], _], source: Graph[SourceShape[O], _]): Flow[I, O, NotUsed] =
    fromSinkAndSourceMat(sink, source)(Keep.none)

This Flow is opposite from Sink to Source in terms of flow direction. The upstream and downstream of the Flow can not be coordinated, that is, the end signal of Source can not reach Sink, because the two ends are independent of each other. We have to solve this problem with a Flow constructed from the fromSinkAndSource function in the CoupledTermination object:

/**
 * Allows coupling termination (cancellation, completion, erroring) of Sinks and Sources while creating a Flow them them.
 * Similar to `Flow.fromSinkAndSource` however that API does not connect the completion signals of the wrapped stages.
 */
object CoupledTerminationFlow {
  @deprecated("Use `Flow.fromSinkAndSourceCoupledMat(..., ...)(Keep.both)` instead", "2.5.2")
  def fromSinkAndSource[I, O, M1, M2](in: Sink[I, M1], out: Source[O, M2]): Flow[I, O, (M1, M2)] =
    Flow.fromSinkAndSourceCoupledMat(in, out)(Keep.both)
 

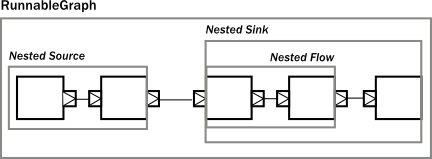
As you can see from Composite BidiFlow in the column above, the interior of a composite Graph can be very complex, but only a few simple input and output ports can be seen from the outside. However, the ports between Graph internals must be properly connected according to functional logic, and the rest will be directly exposed to the outside world. This mechanism supports a hierarchical modular combination approach, as shown in the following illustrations:

Finally, it becomes:

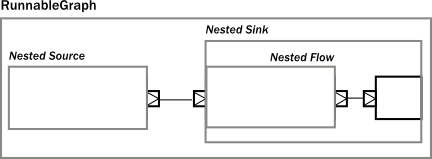
In DSL, we can use name("??") to divide modules:

val nestedFlow =
  Flow[Int].filter(_ != 0) // an atomic processing stage
    .map(_ - 2) // another atomic processing stage
    .named("nestedFlow") // wraps up the Flow, and gives it a name

val nestedSink =
  nestedFlow.to(Sink.fold(0)(_ + _)) // wire an atomic sink to the nestedFlow
    .named("nestedSink") // wrap it up

// Create a RunnableGraph
val runnableGraph = nestedSource.to(nestedSink)

In the following demonstration, we customize a flow chart module for some function: it has two inputs and three outputs. Then we use this custom flow graph module to construct a complete closed flow graph:

import akka.actor._
import akka.stream._
import akka.stream.scaladsl._

import scala.collection.immutable

object GraphModules {
  def someProcess[I, O]: I => O = i => i.asInstanceOf[O]

  case class TwoThreeShape[I, I2, O, O2, O3](
                                              in1: Inlet[I],
                                              in2: Inlet[I2],
                                              out1: Outlet[O],
                                              out2: Outlet[O2],
                                              out3: Outlet[O3]) extends Shape {

    override def inlets: immutable.Seq[Inlet[_]] = in1 :: in2 :: Nil

    override def outlets: immutable.Seq[Outlet[_]] = out1 :: out2 :: out3 :: Nil

    override def deepCopy(): Shape = TwoThreeShape(
      in1.carbonCopy(),
      in2.carbonCopy(),
      out1.carbonCopy(),
      out2.carbonCopy(),
      out3.carbonCopy()
    )
  }
//a functional module with 2 input 3 output
  def TwoThreeGraph[I, I2, O, O2, O3] = GraphDSL.create() { implicit builder =>
    val balancer = builder.add(Balance[I](2))
    val flow = builder.add(Flow[I2].map(someProcess[I2, O2]))

    TwoThreeShape(balancer.in, flow.in, balancer.out(0), balancer.out(1), flow.out)
  }

  val closedGraph = GraphDSL.create() {implicit builder =>
    import GraphDSL.Implicits._
    val inp1 = builder.add(Source(List(1,2,3))).out
    val inp2 = builder.add(Source(List(10,20,30))).out
    val merge = builder.add(Merge[Int](2))
    val mod23 = builder.add(TwoThreeGraph[Int,Int,Int,Int,Int])

     inp1 ~> mod23.in1
     inp2 ~> mod23.in2
     mod23.out1 ~> merge.in(0)
     mod23.out2 ~> merge.in(1)
     mod23.out3 ~> Sink.foreach(println)
     merge ~> Sink.foreach(println)
     ClosedShape

  }
}

object TailorGraph extends App {
  import GraphModules._

  implicit val sys = ActorSystem("streamSys")
  implicit val ec = sys.dispatcher
  implicit val mat = ActorMaterializer()

  RunnableGraph.fromGraph(closedGraph).run()

  scala.io.StdIn.readLine()
  sys.terminate()


}

This custom TwoThreeGraph is a composite flow chart module that can be reused. Note the use of this ~> conformance: akka-stream only provides support for preset Shape as a connection object, such as:

      def ~>[Out](junction: UniformFanInShape[T, Out])(implicit b: Builder[_]): PortOps[Out] = {...}
      def ~>[Out](junction: UniformFanOutShape[T, Out])(implicit b: Builder[_]): PortOps[Out] = {...}
      def ~>[Out](flow: FlowShape[T, Out])(implicit b: Builder[_]): PortOps[Out] = {...}
      def ~>(to: Graph[SinkShape[T], _])(implicit b: Builder[_]): Unit =
        b.addEdge(importAndGetPort(b), b.add(to).in)

      def ~>(to: SinkShape[T])(implicit b: Builder[_]): Unit =
        b.addEdge(importAndGetPort(b), to.in)
...

So for our custom TwoThreeShape, we can only use direct port connections:

   def ~>[U >: T](to: Inlet[U])(implicit b: Builder[_]): Unit =
        b.addEdge(importAndGetPort(b), to)

The above process shows that the construction of composite Graph can be visualized through akka's GraphDSL, and most of the work is on how to connect the ports between components. Let's look at the construction process of a more complex composite flow graph. Here's an illustration of this flow graph:

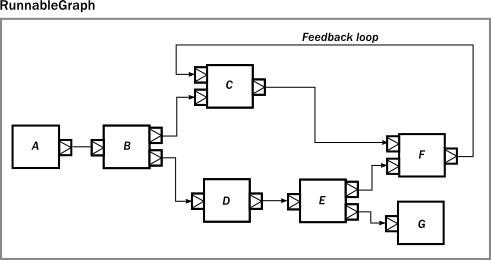
It can be said that this is a relatively complex data processing scheme, which even includes a data flow loop (feedback). It's impossible to imagine how scalaz-stream, a pure functional data stream, can be used to implement such a complex process, or there may be no solution at all. But akka GraphDSL can be used to combine this data flow graph visually.

  import GraphDSL.Implicits._
  RunnableGraph.fromGraph(GraphDSL.create() { implicit builder =>
    val A: Outlet[Int]                  = builder.add(Source.single(0)).out
    val B: UniformFanOutShape[Int, Int] = builder.add(Broadcast[Int](2))
    val C: UniformFanInShape[Int, Int]  = builder.add(Merge[Int](2))
    val D: FlowShape[Int, Int]          = builder.add(Flow[Int].map(_ + 1))
    val E: UniformFanOutShape[Int, Int] = builder.add(Balance[Int](2))
    val F: UniformFanInShape[Int, Int]  = builder.add(Merge[Int](2))
    val G: Inlet[Any]                   = builder.add(Sink.foreach(println)).in

    C     <~      F
    A  ~>  B  ~>  C     ~>      F
    B  ~>  D  ~>  E  ~>  F
    E  ~>  G

    ClosedShape
  })

Another version of port connection is as follows:

RunnableGraph.fromGraph(GraphDSL.create() { implicit builder =>
  val B = builder.add(Broadcast[Int](2))
  val C = builder.add(Merge[Int](2))
  val E = builder.add(Balance[Int](2))
  val F = builder.add(Merge[Int](2))

  Source.single(0) ~> B.in; B.out(0) ~> C.in(1); C.out ~> F.in(0)
  C.in(0) <~ F.out

  B.out(1).map(_ + 1) ~> E.in; E.out(0) ~> F.in(1)
  E.out(1) ~> Sink.foreach(println)
  ClosedShape
})

If you divide the complex Graph above into modules, part of it is as follows:

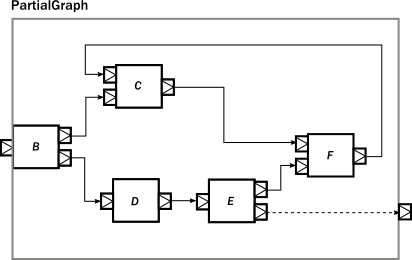
val partial = GraphDSL.create() { implicit builder =>
    val B = builder.add(Broadcast[Int](2))
    val C = builder.add(Merge[Int](2))
    val E = builder.add(Balance[Int](2))
    val F = builder.add(Merge[Int](2))

    C  <~  F
    B  ~>                            C  ~>  F
    B  ~>  Flow[Int].map(_ + 1)  ~>  E  ~>  F
    FlowShape(B.in, E.out(1))
  }.named("partial")

This part can be implemented with the following code:

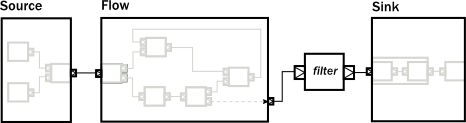
// Convert the partial graph of FlowShape to a Flow to get
// access to the fluid DSL (for example to be able to call .filter())
val flow = Flow.fromGraph(partial)

// Simple way to create a graph backed Source
val source = Source.fromGraph( GraphDSL.create() { implicit builder =>
  val merge = builder.add(Merge[Int](2))
  Source.single(0)      ~> merge
  Source(List(2, 3, 4)) ~> merge

  // Exposing exactly one output port
  SourceShape(merge.out)
})

// Building a Sink with a nested Flow, using the fluid DSL
val sink = {
  val nestedFlow = Flow[Int].map(_ * 2).drop(10).named("nestedFlow")
  nestedFlow.to(Sink.head)
}

// Putting all together
val closed = source.via(flow.filter(_ > 1)).to(sink)

Unlike scalaz-stream, akka-stream is operated on actors. in addition to data stream elements, akka-stream can also maintain and return operation results through the internal state of actors. The process of propagation of this operation result in the composite flow graph is controllable, as shown in the following figure:

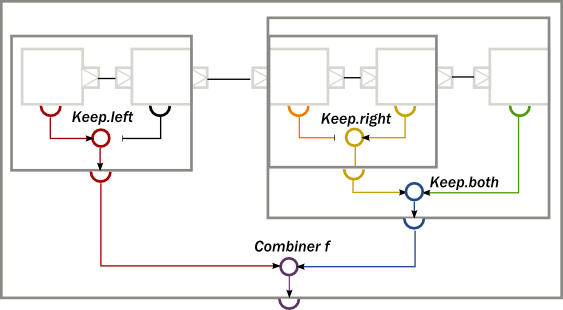
The result of return operation is realized by viaMat and toMat. Short via,to default to select the result of the left-hand operation of the flow graph.