1, DFS

There are two important concepts in DFS: backtracking and pruning
When the weight of all edges in the graph is 1, the BFS must find the shortest path
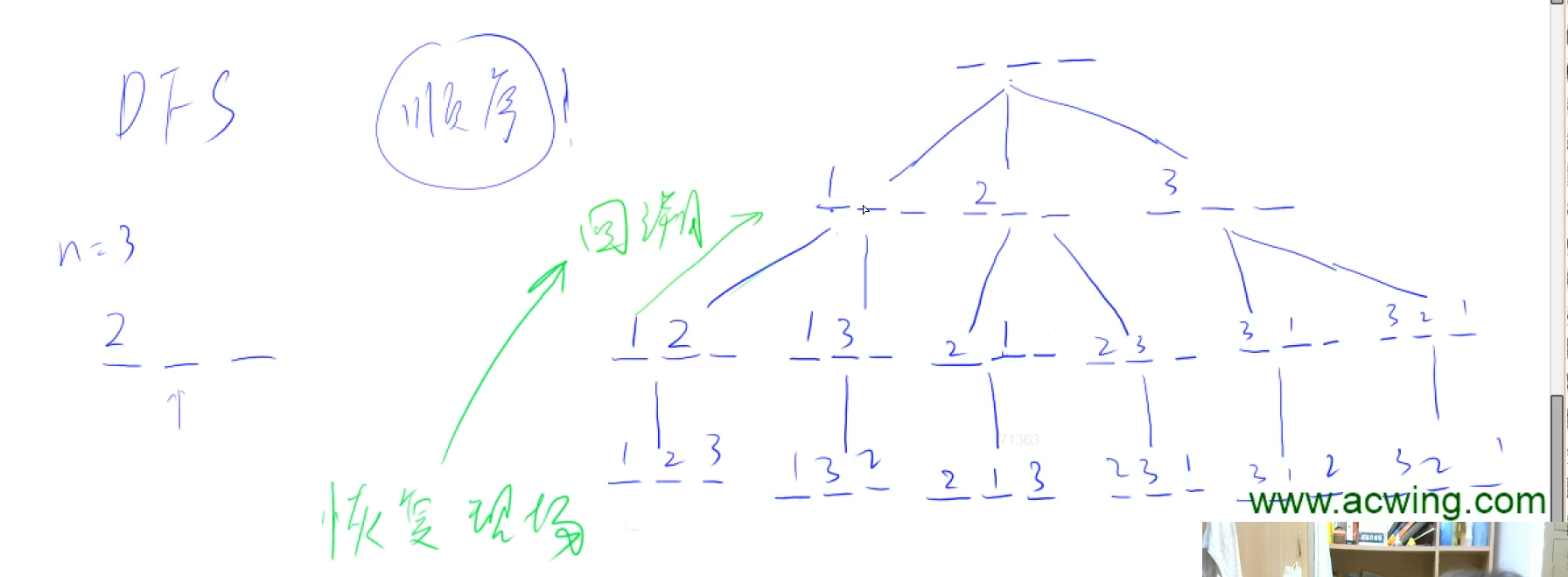
When tracing back, we must pay attention to restoring the scene
Arrange numbers
#include<iostream>
using namespace std;
const int N = 10;
int n;
int path[N];//Record all search paths
bool st[N];//Record whether these points have been used. 1 means yes and 0 means No
void dfs(int u) // Layer u
{
if(u == n)//Starting from 0 as the first layer, when the last layer is searched, the path is output and the recursion ends
{
for(int i=0;i<n;i++)
{
printf("%d ",path[i]);
}
puts("");
return;
}
for(int i=1;i<=n;i++)
{
if(!st[i])
{
path[u] = i;//Write path record
st[i] = true;//Update status is used
dfs(u+1);//Find the number for the next floor
//----------------------------------The next level of recursion ends, and it's time to restore the state
st[i] = false;//Update status is not used
path[u] = 0;//Clear the layer path record
}
}
}
int main()
{
cin>>n;
dfs(0);
return 0;
}
Pruning: if you judge in advance that the current scheme must be illegal, there is no need to search down and go back directly
There are 16 positive diagonals and 16 reverse diagonals in the figure
Positive diagonal: a straight line with a slope of - 1 and passing through the point
Inverse diagonal: a straight line with a slope of 1 and passing through the point
#include<iostream>
using namespace std;
const int N = 10;
int n;
char g[N][N];//Recording scheme
bool col[N],dj[2*N],fdj[2*N];//Same row (column), positive diagonal, reverse diagonal
void dfs(int u)
{
if(u == n)//When the last row and leaf node are searched, the scheme is output
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
printf("%c",g[i][j]);
}
puts("");
}
puts("");
return;
}
for(int i = 0;i < n;i++)//Enumerate i:x u:y from the first column x
{
if(!col[i] && !dj[i+u] && !fdj[n + u - i])//Prevent the opposition angle from being negative and add n to the normal range
{
g[u][i] = 'Q';//Place queen
col[i] = dj[i+u] = fdj[u-i+n] = true;//Status update
dfs(u+1);//Search next column
//Restore state to prepare for backtracking
g[u][i] = '.';
col[i] = dj[i+u] = fdj[u-i+n] = false;
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
g[i][j] = '.';//initialization
}
}
dfs(0);
return 0;
}
2, BFS
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int M = 105;
typedef pair<int,int> PII;
queue<PII>q;
int n,m;
int g[M][M];
int cnt[M][M];//Stores the number of steps taken to each point
int dx[4] = {0,0,-1,1};//x direction
int dy[4] = {1,-1,0,0};//y direction: up, down, left and right
int bfs()
{
q.push({0,0});
cnt[0][0] = 0;
while(!q.empty())
{
PII pos = q.front();
q.pop();
for(int i=0;i<4;i++)
{
int y = pos.first + dy[i];
int x = pos.second + dx[i];
if(x>=0 && x< m && y>=0 && y<n && g[y][x] == 0 && cnt[y][x] == -1) //Within the range, not a wall, and did not walk through
{
q.push({y,x});
cnt[y][x] = cnt[pos.first][pos.second] + 1; //The number of steps at this point is equal to the number of steps at the previous point plus 1
}
}
}
return cnt[n-1][m-1];//Returns the number of steps for the exit point
}
int main()
{
cin>>n>>m;//For graphs with all edge weights of 1, bfs can find the shortest path, but it can't go back (go twice at a point)
memset(cnt,-1,sizeof cnt);//Initialize the cnt array to - 1, indicating that the point has not been passed
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>g[i][j];
}
}
cout<<bfs()<<endl;
return 0;
}
Output path
if(x>=0 && x< m && y>=0 && y<n && g[y][x] == 0 && cnt[y][x] == -1) //Within the range, not a wall, and did not walk through
{
q.push({y,x});
cnt[y][x] = cnt[pos.first][pos.second] + 1; //The number of steps at this point is equal to the number of steps at the previous point plus 1
Prev[y][x] = pos;
}
PII Prev[M][M];
while(i || j)
{
cout<<i<<" "<<j<<endl;
pos = Prev[i][j];
i = pos.first;
j = pos.second;
}
3, Storage of trees and graphs

Edge multipurpose matrix, point multipurpose table
The adjacency table usually selects the head insertion method when inserting
Array analog linked list
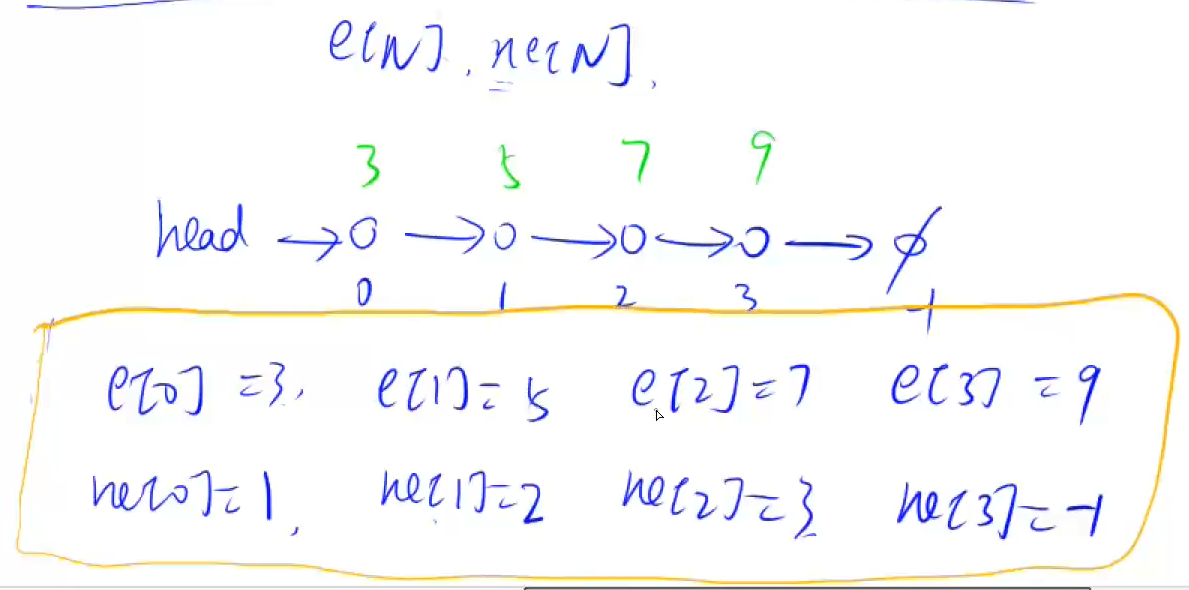
e [] is equivalent to val and ne [] is equivalent to next
4, Priority traversal of trees and graphs
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int h[N],e[2*N],ne[2*N],idx;
bool st[N];
int n;
int ans = N;//Answer: the minimum value of the largest subtree
void add(int a,int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int dfs(int u)
{
st[u] = true;
int sum = 1;//Size of current subtree u
int res = 0;//The maximum number of points in each connected block after deleting the point
for(int i = h[u];i!=-1;i = ne[i])
{
int j = e[i];
if(!st[j])
{
int s = dfs(j);//Current size of this sub tree j
res = max(res,s);
sum += s;//The size of the subtree u is equal to the sum of the subtrees that make up it
}
}
res = max(res,n-sum);//Compare with the subtree where the parent node is located
ans = min(ans,res);//Compare with the answer and update the answer
return sum;//Returns the size of the subtree
}
int main()
{
memset(h,-1,sizeof h);
cin>>n;
for(int i=0;i<n;i++)
{
int a,b;
cin>>a>>b;
add(a,b),add(b,a);//The edges are bidirectional
}
dfs(1);
cout<<ans<<endl;
}
Hierarchy of points in BFS diagram
Classic BFS
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int M = 1e5+10;
int h[M],e[M],ne[M],idx;
int n,m;
int d[M];//Record the distance from the point to the starting point
queue<int>q;
void add(int a,int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx;
idx++;
}
int bfs()
{
q.push(1);
memset(d,-1,sizeof d);
d[1] = 0;//The starting distance is 0
while(!q.empty())
{
int t = q.front();
q.pop();
for(int i = h[t];i != -1;i = ne[i])
{
int j = e[i];
if(d[j] == -1)//If the distance is - 1, it indicates that it has not been traversed before
{
q.push(j);
d[j] = d[t] + 1;//Update the distance, and the distance between adjacent points will be increased by 1
}
}
}
return d[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);//Note: the initialization chain header must be - 1 here, otherwise TLE
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);//Unidirectional edges: a to b
}
cout<<bfs()<<endl;
return 0;
}
5, Topological sequence
Directed acyclic graph must have topological sequence, which is also called topological graph
Penetration: how many edges point to this node
Out degree: the node has several points (several edges)

If there is a ring, all points in the ring will not join the team because no breakthrough can be found
848. Topological sequence of digraph
Note: the answer to this question is not unique. Just output the legal topological order
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int M = 1e5 + 10;
int e[M],ne[M],h[M],idx;
int d[M],q[M],hh=0,tt=-1;//d [] is the penetration of each point. Note: the array simulates the queue, and hh is 0
int n,m,x,y;
void add(int a,int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx;
idx ++;
d[b]++;
}
bool TopSort()//bfs thinking
{
for(int i=1;i<=n;i++)//First queue all points with degree 0 in the graph
{
if(!d[i]) q[++tt] = i;
}
while(tt >= hh)//Queue is not empty
{
int t = q[hh++];//Out of the team
for(int i=h[t];i!=-1;i = ne[i])//Traverse all points pointed to by this point
{
int tmp = e[i];
d[tmp]--;//Delete an edge pointing to the point and reduce the entry by one
if(!d[tmp]) q[++tt] = tmp;//If the entry degree is 0, it indicates that it is the topological order's turn to join the team
}
}
if(tt == n-1) return true;//If all points join the team, it means that it is an acyclic graph
else return false;
}
int main()
{
memset(h,-1,sizeof h);//Be sure to initialize that each header node is empty
cin>>n>>m;
for(int i=0;i<m;i++)
{
cin>>x>>y;
add(x,y);
}
if(TopSort())
{
for(int i=0;i<n;i++)//When leaving the queue, only the head pointer moves, the actual array elements remain unchanged, and the queue order is the topological order
{
cout<<q[i]<<" ";
}
puts("");
}
else puts("-1");
return 0;
}
6, Shortest path algorithm
Source point: start point
Meeting point: end point
Single source shortest path: there is only one starting point
Multi source sink shortest path: multiple starting points
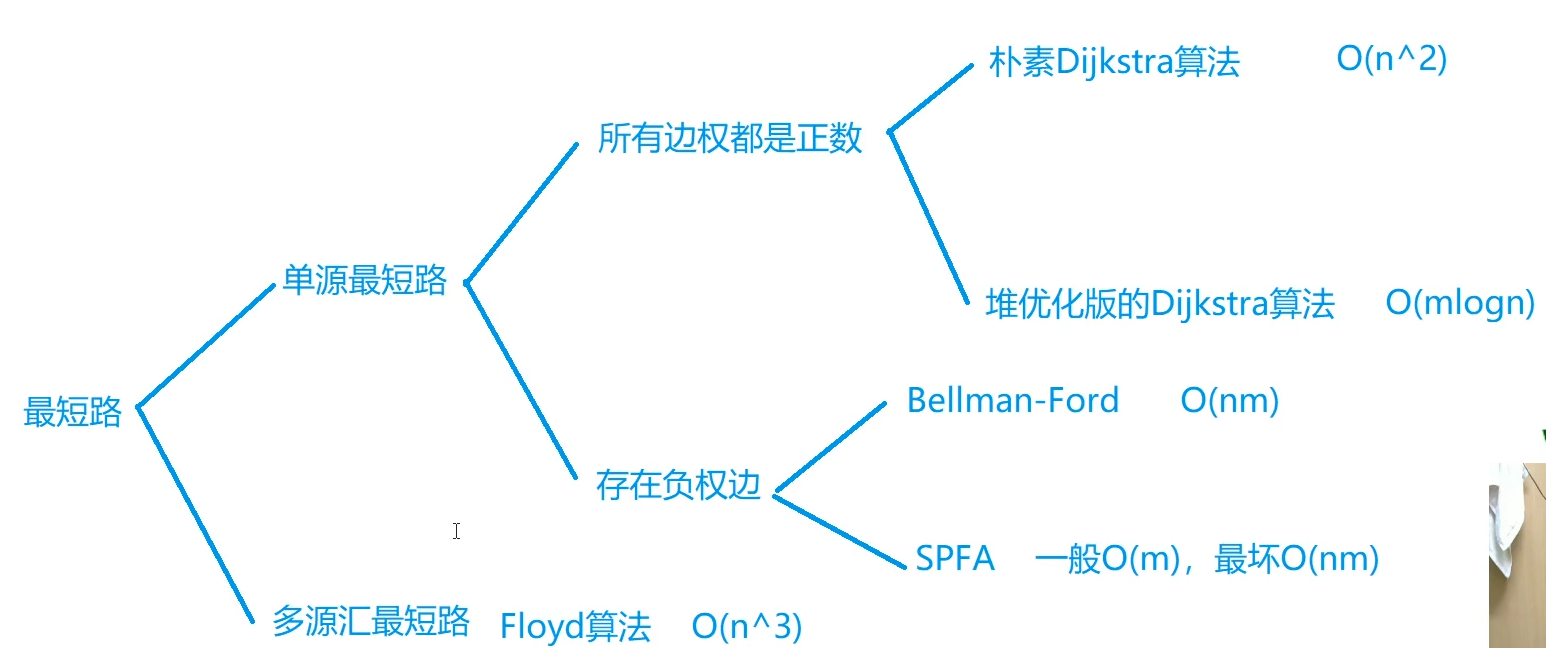
1. Simple dijkstra algorithm
Step 1:
Initialization distance dist[1] = 0,dist[i] = positive infinity
Step 2:
for i :[1,n)
T < - find the nearest point that is not in the set S
S < - t add t to s
Update the distance of other points with t

Dijkstra finding the shortest path I
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 505;
const int INF = 0x3f3f3f3f;//Maximum int value, infinity
int g[N][N]; //Adjacency matrix storage dense graph
int dist[N]; //Distance from point 1 to point n
int n,m,x,y,z;
bool st[N];//Is the shortest distance determined
int Dijkstra()
{
dist[1] = 0;//The starting distance is 0
for(int i=1;i<=n;i++)//n points, n cycles
{
int t = -1;//Stores the point with the smallest distance that is not currently determined
for(int j = 1;j <= n;j++)//o(n) find the point with the smallest distance
{
if(!st[j] && (t==-1 || dist[j] < dist[t]))
{
t = j;
}
}
st[t] = true;//Mark the shortest distance determined
for(int j=1;j<=n;j++)//Use this point to update the shortest distance of all points
{
dist[j] = min(dist[j],dist[t] + g[t][j]);
}
}
if(dist[n] == INF) return -1;//Infinity means there is no path
else return dist[n];
}
int main()
{
cin>>n>>m;
memset(g,INF,sizeof g);//Initialize all paths in the graph to infinity
memset(dist,INF,sizeof dist);//Initialize all distances to infinity
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
g[x][y] = min(g[x][y],z);//There are multiple edges and self rings in the graph, which can be solved by taking the shortest path
}
cout<<Dijkstra()<<endl;
}
Infinite constant commonly used in ACM -- 0x3f3f3f3f
2. dijkstra algorithm of heap optimized version
#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
const int M = 1.5*1e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int,int>PII;//first represents the distance from the starting point, and second represents the number of points
int h[M],e[M],ne[M],w[M],idx;//Sparse graphs are stored using adjacency tables, w[] representing the weights of edges
int n,m,x,y,z;
int dist[M];
bool st[M];
void add(int a,int b,int c)
{
e[idx] = b;
w[idx] = c;//Maintain edge weights
ne[idx] = h[a];
h[a] = idx;
idx++;
}
int Dijkstra()//Heap optimized Dijkstra algorithm, a bit like bfs
{
priority_queue<PII,vector<PII>,greater<PII>>heap;//Define a small root heap
heap.push({0,1});//First, the distance from point 1 is 0 and put into the heap
dist[1] = 0;//ditto
while(!heap.empty())
{
PII t = heap.top();
heap.pop();
int num = t.second,distance = t.first;
if(st[num]) continue;//If the shortest distance has been determined, skip
st[num] = true;//Note: the order in which the status of the shortest distance has been determined is maintained
for(int i = h[num];i!=-1;i=ne[i])//Maintain the shortest distance of adjacent points with the point with the shortest distance determined
{
int num1 = e[i];
if(dist[num1] > distance + w[i])
{
dist[num1] = distance + w[i];
heap.push({dist[num1],num1});
}
}
}
if(dist[n] == INF) return -1;//No access
else return dist[n];
}
int main()
{
memset(h,-1,sizeof h);
memset(dist,INF,sizeof dist);//The initialization linked list is empty, and the shortest distance is infinity
cin>>n>>m;
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
add(x,y,z);
}
cout<<Dijkstra()<<endl;
return 0;
}
3. Bellman Ford algorithm (dealing with negative edge weight)

There may be no negative weight loop in the graph with solution, and the algorithm can find the negative weight loop
Shortest path with edge limit
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 505,M = 10005,INF = 0x3f3f3f3f;
int n,m,k,x,y,z;
int dist[N],backup[N];//backup is used to record the last dist to prevent updating the distance of multiple points in one i cycle
struct edge
{
int x;
int y;
int z;
}Edge[M];
int Bellman_Ford()
{
memset(dist,INF,sizeof dist);//First, update the dist of each point to infinity
dist[1] = 0;//Source distance is 0
for(int i=0;i<k;i++)//The title requires a maximum of k edges
{
memcpy(backup,dist,sizeof dist);//Copy dist after the last i cycle to backup
for(int j=0;j<m;j++)
{
int a = Edge[j].x;
int b = Edge[j].y;
int w = Edge[j].z;
dist[b] = min(dist[b],backup[a] + w);
}
}
if(dist[n] >= INF/2) return -2;//Because there is a negative edge, when the meaning of the question is not satisfied, the end distance is not necessarily infinity
//But it must be a large number
else return dist[n];
}
int main()
{
cin>>n>>m>>k;
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
Edge[i] = {x,y,z};
}
int t = Bellman_Ford();
if(t == -2) puts("impossible");
else cout<<t<<endl;
return 0;
}
4.SPFA algorithm (used more)
spfa finding the shortest path
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int M = 1e5+10,INF = 0x3f3f3f3f;
int h[M],e[M],w[M],ne[M],idx;
int dist[M];
bool st[M];//Indicates whether the point is in the queue. 1 is yes and 0 is No
int n,m,x,y,z;
void add(int a,int b,int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
idx++;
}
int spfa()//The idea is similar to dijkstra algorithm, but the difference lies in the meaning of st
{
memset(dist,INF,sizeof dist);
dist[1] = 0;
queue<int>q;
q.push(1);
st[1] = true;
while(!q.empty())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];//In case of distance update
if(!st[j])//And the point is not in the queue
{
q.push(j);//Join the team and update st[j] the status
st[j] = true;
}
}
}
}
if(dist[n] == INF) return -2;//Returning to - 1 will wa drop, and there may be a negative edge
else return dist[n];
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
add(x,y,z);
}
int t = spfa();
if(t==-2) puts("impossible");
else cout<<t<<endl;
return 0;
}
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int M = 1e5+10,INF = 0x3f3f3f3f;
int h[M],e[M],w[M],ne[M],idx;
int dist[M],cnt[M];//Record the number of edges in the path from point 1 to point n
bool st[M];//Indicates whether the point is in the queue. 1 is yes and 0 is No
int n,m,x,y,z;
void add(int a,int b,int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
idx++;
}
bool spfa()//spfa algorithm to find whether there is a negative ring, the idea comes from the drawer method
{
memset(dist,INF,sizeof dist);
//dist[1] = 0;
queue<int>q;
for(int i=1;i<=n;i++)//Because you may not be able to get to point n from point 1, you must join the team at each point at first
{
q.push(i);
st[i] = true;
}
while(!q.empty())
{
int t = q.front();
q.pop();
st[t] = false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j = e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];//If a distance update occurs and the point is not in the queue
cnt[j] = cnt[t] + 1;//The number of adjacent points differs by 1
if(cnt[j] >= n) return true;//If the number of edges on the path is greater than or equal to the number of all points, there must be a negative ring
if(!st[j])
{
q.push(j);//Join the team and update st[j] the status
st[j] = true;
}
}
}
}
return false;//No negative ring
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++)
{
cin>>x>>y>>z;
add(x,y,z);
}
if(spfa()) puts("Yes");
else puts("No");
return 0;
}
Floyd algorithm (O^3)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 205,INF = 0x3f3f3f3f;
int n,m,x,y,z,k;
int d[N][N];
void Floyd() //dynamic programming
{
for(int k=1;k<=n;k++) //k must be in the outer loop, and the order of I and j loops is variable
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
d[i][j] = min(d[i][j],d[i][k] + d[k][j]);
}
}
}
}
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)//Initialize distance array
{
for(int j=1;j<=n;j++)
{
if(i == j) d[i][j] = 0;//The same point distance is 0
else d[i][j] = INF;//Otherwise set to infinity
}
}
for(int i=1;i<=m;i++)
{
cin>>x>>y>>z;
d[x][y] = min(d[x][y],z);//If there are multiple edges, the edge with the smallest distance shall prevail
}
Floyd();
while(k--)
{
cin>>x>>y;
if(d[x][y] >= INF/2) puts("impossible");//There is a negative edge, so the path distance is not necessarily infinite
else cout<<d[x][y]<<endl;
}
return 0;
}
7, Minimum spanning tree
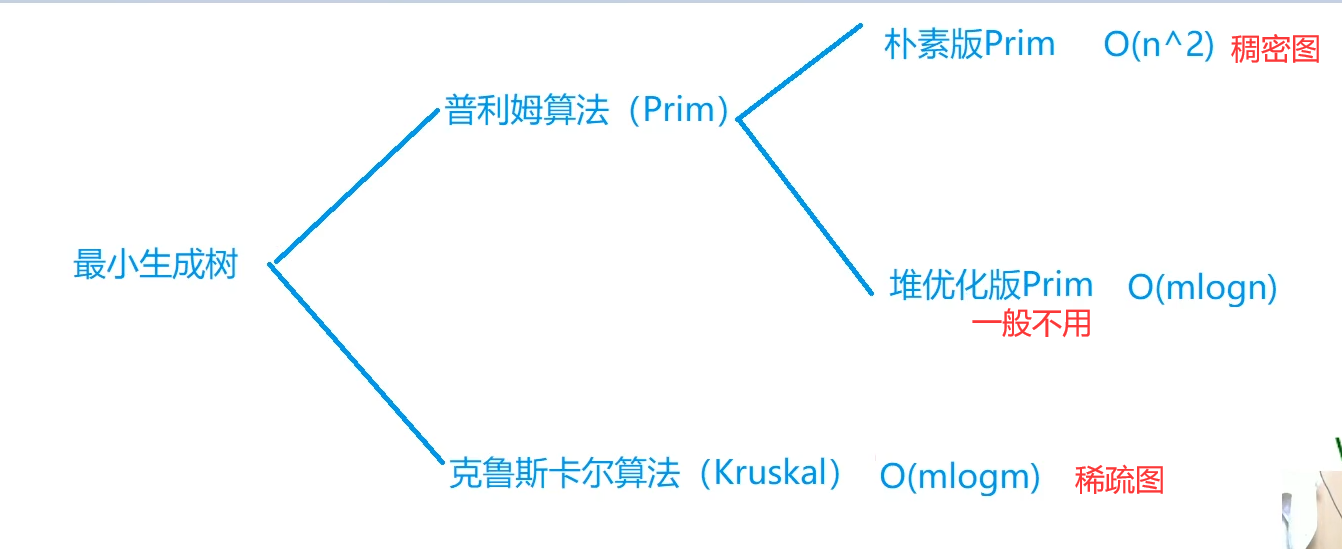

Naive Prim algorithm (O^2)

858. Prim algorithm for minimum spanning tree
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 505,INF = 0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];//Represents the distance from a point to a point in the collection
bool st[N];
int prim()
{
int res = 0;
memset(dist,INF,sizeof dist);
for(int i=0;i<n;i++)
{
int t = -1;
for(int j=1;j<=n;j++)
{
if(!st[j] && (t == -1 || dist[j] < dist[t])) //J is outside the set, and no point is found or j distance is small
{
t = j;
}
}
if(i && dist[t] == INF) return INF; //Not the first point and the distance from the nearest point is infinite,
//Illustration diagram is not connected
if(i) res += dist[t];//As long as it's not the first side, add the distance of t to the answer
for(int j=1;j<=n;j++)
{
dist[j] = min(dist[j],g[t][j]);
}
st[t] = true; //Indicates that the current point is added to the collection
}
return res;
}
int main()
{
cin>>n>>m;
memset(g,INF,sizeof g);
for(int i=0;i<m;i++)
{
int a,b,c;
cin>>a>>b>>c;
g[a][b] = g[b][a] = min(c,g[a][b]);//Undirected graph
}
int t = prim();
if(t == INF) puts("impossible");
else cout<<t<<endl;
return 0;
}
Kruskal algorithm (fast sorting + joint search set)

859. Kruskal algorithm for minimum spanning tree
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int M = 2e5+20,INF = 0x3f3f3f3f;
int p[M];
int n,m,a,b,c;
struct Edge
{
int a;
int b;
int w;
}edges[M];
int find(int a) //Find the ancestor of the collection of point a
{
if(a!=p[a]) p[a] = find(p[a]);
return p[a];
}
bool cmp(struct Edge a,struct Edge b)
{
return a.w < b.w;
}
void kruskal()
{
int cnt = 0,res = 0;
sort(edges+1,edges+m+1,cmp);//Sort each edge in ascending order
for(int i=1;i<=n;i++) //Initialize all collections
{
p[i] = i;
}
for(int i=1;i<=m;i++)
{
int a = edges[i].a;
int b = edges[i].b;
int w = edges[i].w;
a = find(a),b = find(b); //If not in a set, merge
if(a!=b)
{
p[b] = a;
cnt++;
res += w;
}
}
if(cnt < n-1) puts("impossible");//The merging times are less than n-1, indicating that the graph is not connected
else cout<<res<<endl;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
edges[i] = {a,b,c};
}
kruskal();
return 0;
}
Determination of bipartite graph by coloring method
Bipartite graph, also known as bipartite graph, is a special model in graph theory. Let G=(V,E) be an undirected graph. If vertex v can be divided into two disjoint subsets (A,B), and the two vertices i and j associated with each edge (i, J) in the graph belong to these two different vertex sets (i in A,j in B), then graph G is called a bipartite graph.
Bipartite graph if and only if the graph does not contain odd rings
Determination of bipartite graph by coloring method
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10; // Undirected graph, so the maximum number of edges is 2 times
int e[M], ne[M], h[N], idx;
int st[N];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool dfs(int u, int color) {
st[u] = color;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(!st[j]) {
if(!dfs(j, 3 - color)) return false;
}else if(st[j] == color) return false;
}
return true;
}
int main(){
int n, m;
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m --){
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b,a); // Undirected graph
}
bool flag = true;
for(int i = 1; i <= n; i ++){
if(!st[i]){
if(!dfs(i, 1)){
flag = false;
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}

