131. The largest rectangle in the histogram - AcWing question bank

Title Description

tag: monotone stack

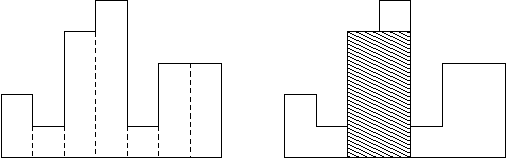
A histogram is a polygon consisting of a series of rectangles aligned at a common baseline.

Rectangles have equal widths, but can have different heights.

For example, the left side of the legend shows a histogram composed of rectangles with heights of 2,1,4,5,1,3,3, and the width of each rectangle is 1:

Input format

The input contains several test cases.

Each test case occupies a line to describe a histogram, and starts with the integer n to represent the number of rectangles constituting the histogram.

Then followed by n integers h 1 ， ... ， h n h_1，...，h_n h1​，...，hn​.

These numbers represent the height of each rectangle of the histogram in order from left to right.

Each rectangle has a width of 1.

Line numbers are separated by spaces.

When the input case is n=0, the input is ended, and the case is not considered.

Output format

For each test case, output an integer representing the area of the largest rectangle in the specified histogram.

Each data occupies one row.

Note that this rectangle must be aligned at a common baseline.

Data range

1≤n≤100000
0 ≤ h i ≤ 1000000000 0≤h_i≤1000000000 0≤hi​≤1000000000

Sample

Input example:

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Output example:

8
4000

The meaning of the question is that let's find the maximum rectangular area.

We can start by thinking about the simplest way. The area of a rectangle has two properties, width and height. We can get the height at one time through the read data, but we need to enumerate the width of the rectangle.

That is, for a rectangle at i position, we need to find the first one on the left that is lower than it and the first one on the right that is lower than it.

Then we can write violent algorithms.

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int q[N];

int main(int argc, char const *argv[])
{
    int n;
    while (scanf("%d", &n), n)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", q + i);

        int res = 0;
        for (int i = 0; i < n; i++)
        {
            int l = i, r = i;
            // Find left boundary
            while (l >= 0 && q[l] > q[i])
                l--;
            // Find left boundary
            while (r < n && q[r] > q[i])
                r++;
            // After finding the left and right boundaries, you can start to calculate the area of the
            int s = (r - l - 1) * q[i];
            res = max(res, s);
        }
		
        printf("%d\n", res);
    }
    return 0;
}

But what is the time complexity?

Obviously, yes O ( N 2 ) O(N^2) O(N2), so how should we optimize it? We can find that the most time-consuming operation is to find the left and right boundaries. So how should we optimize it?

Taking finding the left boundary as an example, we can find that when the rectangle on the right of a rectangle is lower than it, then the rectangle cannot be the first lower than it, because the rectangle on the right of the current rectangle will be found first, not the rectangle on the left, so this is an obvious monotonic stack. We need to eliminate the elements that must not be boundaries in each search process, so as to speed up our search

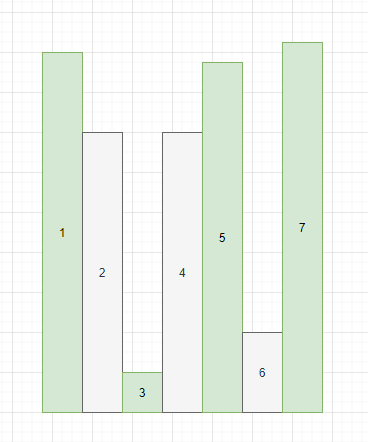
Like the figure above, the left boundary of 4 must be 3, and the left boundary of 5 must be 3. It can't be 1 and 2, because 3 is smaller than 1 and 2, and it's still behind.

Therefore, the code implemented by monotone stack is finally used

#include <iostream>
using namespace std;

typedef long long ll;
const int N = 1e5 + 10;
int q[N], stk[N], tt = -1, l[N], r[N];

int main(int argc, char const *argv[])
{
    int n;
    while (scanf("%d", &n), n)
    {
        for (int i = 1; i <= n; i++)
            scanf("%d", q + i);
        // Find l, initialize the stack, and make the first element of the stack - 1 at the beginning,
        // It must be smaller than all elements to avoid boundary problems
        tt = 0;
        stk[0] = 0;
        q[0] = -1;
        for (int i = 1; i <= n; i++)
        {
            // When the current element is less than or equal to the top element of the stack
            while (q[stk[tt]] >= q[i])
                // Stack element pop-up --- the pop-up element cannot be used as the left boundary behind. After pop-up, speed up the search
                tt--;
            l[i] = stk[tt];
            stk[++tt] = i;
        }
        // Similarly, find r
        tt = 0;
        stk[0] = n + 1;
        q[n + 1] = -1;
        for (int i = n; i >= 1; i--)
        {
            while (q[stk[tt]] >= q[i])
                tt--;
            r[i] = stk[tt];
            stk[++tt] = i;
        }

        // Post group calculation results
        ll res = 0;
        for (int i = 1; i <= n; i++)
            res = max(res, q[i] * (r[i] - l[i] - 1ll));
        printf("%lld\n", res);
    }
    return 0;
}

Of course, we can also optimize again. Due to the monotonous nature, we can use binary search, which can make the search speed faster. The code is as follows

#include <iostream>
using namespace std;

typedef long long ll;
const int N = 1e5 + 10;
int q[N], stk[N], tt = -1, l[N], r[N];

int find(int x)
{
    int l = 0, r = tt;
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (q[stk[mid]] >= x)
            r = mid - 1;
        else
            l = mid;
    }
    return l;
}

int main(int argc, char const *argv[])
{
    int n;
    while (scanf("%d", &n), n)
    {
        for (int i = 1; i <= n; i++)
            scanf("%d", q + i);
        // Find l, initialize the stack, and make the first element of the stack - 1 at the beginning,
        // It must be smaller than all elements to avoid boundary problems
        tt = 0;
        stk[0] = 0;
        q[0] = -1;
        for (int i = 1; i <= n; i++)
        {
            tt = find(q[i]); // Binary search
            l[i] = stk[tt];
            stk[++tt] = i;
        }
        // Similarly, find r
        tt = 0;
        stk[0] = n + 1;
        q[n + 1] = -1;
        for (int i = n; i >= 1; i--)
        {
            tt = find(q[i]); // Binary search
            r[i] = stk[tt];
            stk[++tt] = i;
        }

        // Post group calculation results
        ll res = 0;
        for (int i = 1; i <= n; i++)
            res = max(res, q[i] * (r[i] - l[i] - 1ll));
        printf("%lld\n", res);
    }
    return 0;
}