(please leave a message or chat privately if you have any questions

Catalog

Problem: Portal portal portal

The original title is described at the bottom.
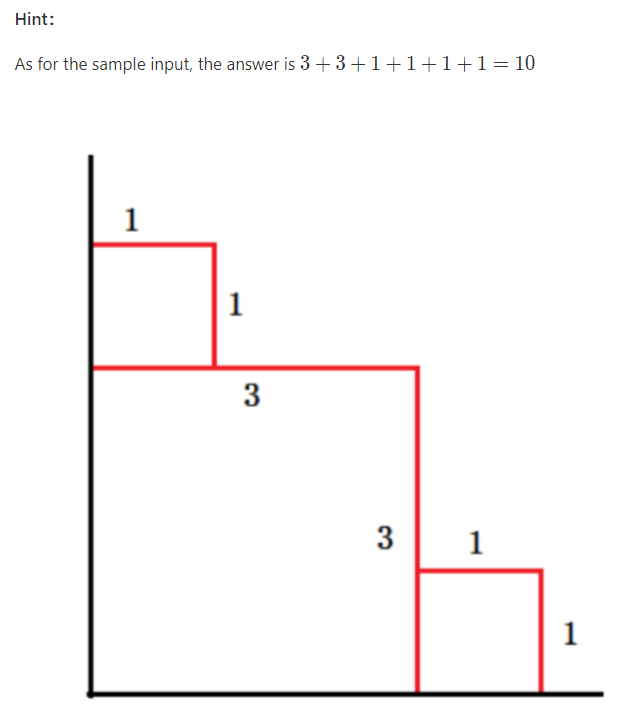
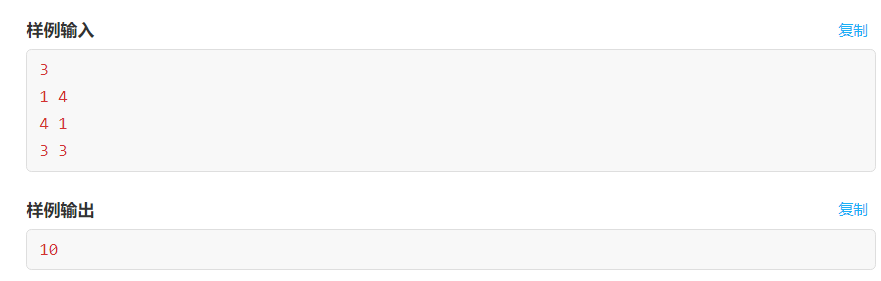
I understand that there are n n tides and ebbs. The range of each time is a rectangle of x × yx × y. find the length of the tide trace after n tides and ebbs.
There is no such i,j ∈ [1,n],i ≠ j,xi ≤ xj and yi ≤ yji,j ∈ [1,n],i ≠ j,xi ≤ xj and yi ≤ yj

Solution:

  each tide may wash away some traces of the previous tide, but it will not wash completely.
  consider to calculate the contribution from the last tide forward, in x and y directions.
  assuming that the range of this tide is [xi,yi][xi,yi], find out the maximum YY greater than or equal to xixi, then the length of new traces in the direction of YY is yi − Yyi − Y, the same is true for the direction of xx.
In this way, the problem is transformed into a problem of finding the maximum value of an interval, which is the second of a line tree.

AC_Code:

#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
const int mod = 1e9+7;
const int MXN = 1e6 + 7;
int n;
int sumx[MXN<<2], sumy[MXN<<2];
int ar[MXN], br[MXN], le[MXN], ri[MXN];
void update(int op,int p,int c,int l,int r,int rt){
    if(l == r){
        if(op == 1) sumx[rt] = max(c,sumx[rt]);
        else sumy[rt] = max(c,sumy[rt]);
        return;
    }
    int mid = (l+r)>>1;
    if(p<=mid)update(op,p,c,l,mid,lson);
    else update(op,p,c,mid+1,r,rson);
    if(op == 1)sumx[rt] = max(sumx[lson], sumx[rson]);
    else sumy[rt] = max(sumy[lson], sumy[rson]);
}
int query(int op,int L,int R,int l,int r,int rt){
    if(L<=l&&r<=R){
        if(op == 1) return sumx[rt];
        else return sumy[rt];
    }
    int mid = (l+r)>>1;
    if(L>mid)return query(op,L,R,mid+1,r,rson);
    else if(R<=mid)return query(op,L,R,l,mid,lson);
    else {
        return max(query(op,L,mid,l,mid,lson),query(op,mid+1,R,mid+1,r,rson));
    }
}
int main(int argc, char const *argv[]){
    scanf("%d", &n);
    int k = 0;
    for(int i = 1; i <= n; ++i){
        scanf("%d%d", &le[i], &ri[i]);
        ar[k++] = le[i];
        ar[k++] = ri[i];
    }
    sort(ar, ar + k);
    k = unique(ar, ar + k) - ar;
    memset(sumx, 0, sizeof(sumx));
    memset(sumy, 0, sizeof(sumy));
    LL ans = 0;
    for(int i = n; i >= 1; --i){
        int a = le[i], b = ri[i];
        le[i] = lower_bound(ar, ar + k, le[i]) - ar + 1;
        ri[i] = lower_bound(ar, ar + k, ri[i]) - ar + 1;
        int my = query(1, le[i], k, 1, k, 1);//Find the maximum Y greater than xi
        ans += b - my;
        int mx = query(2, ri[i], k, 1, k, 1);//Find the maximum X greater than yi
        ans += a - mx;
        //printf("%d %d\n", mx, my);
        update(1, le[i], ar[ri[i]-1], 1, k, 1);//Update yi under this xi
        update(2, ri[i], ar[le[i]-1], 1, k, 1);
    }
    printf("%lld\n", ans);
    return 0;
}

Problem Description: