Reproduced from: About ArrayBlockingQueue

1, introduction

ArrayBlockingQueue, as the name implies: array based blocking queue. Array is to specify the length, so you must specify the length when using ArrayBlockingQueue, that is, it is a bounded queue.

It implements the BlockingQueue interface, with all methods of queue, collection and blocking queue. The queue class diagram is shown in the figure below (the picture comes from the previous article: About Queue:

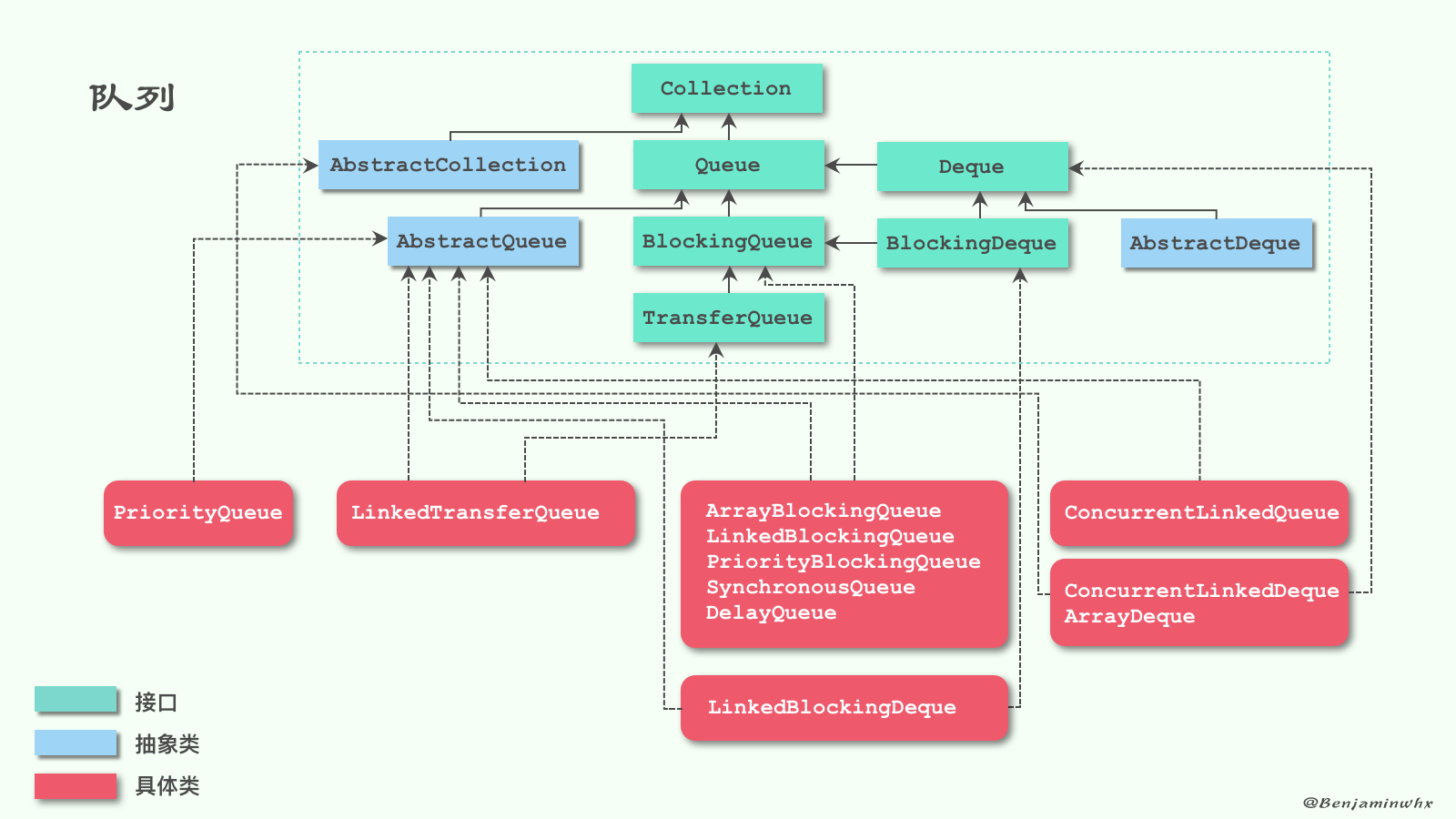
Since it is in the JUC package, it indicates that it is thread safe to use it, and it internally uses ReentrantLock to ensure thread safety. ArrayBlockingQueue supports fair scheduling of producer and consumer threads. Fairness is not guaranteed by default. Fairness usually reduces throughput, but reduces variability and avoids thread starvation.

2. Data structure

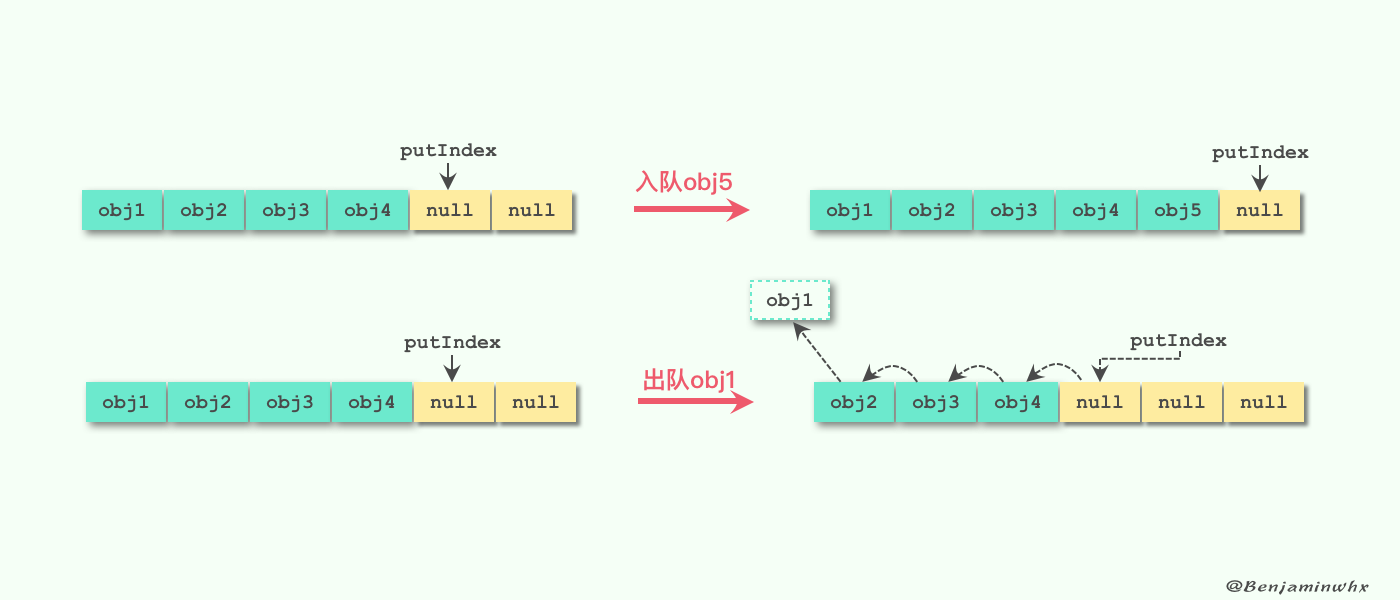
Generally, there are two ways to implement queues: array and linked list. For the implementation of array, we can maintain a queue end pointer so that it can be completed in the O(1) time when entering the queue; however, for the out of queue operation, after deleting the queue head element, we must move all elements in the array forward one position. The complexity of this operation reaches O(n), and the effect is not very good. As shown in the figure below:

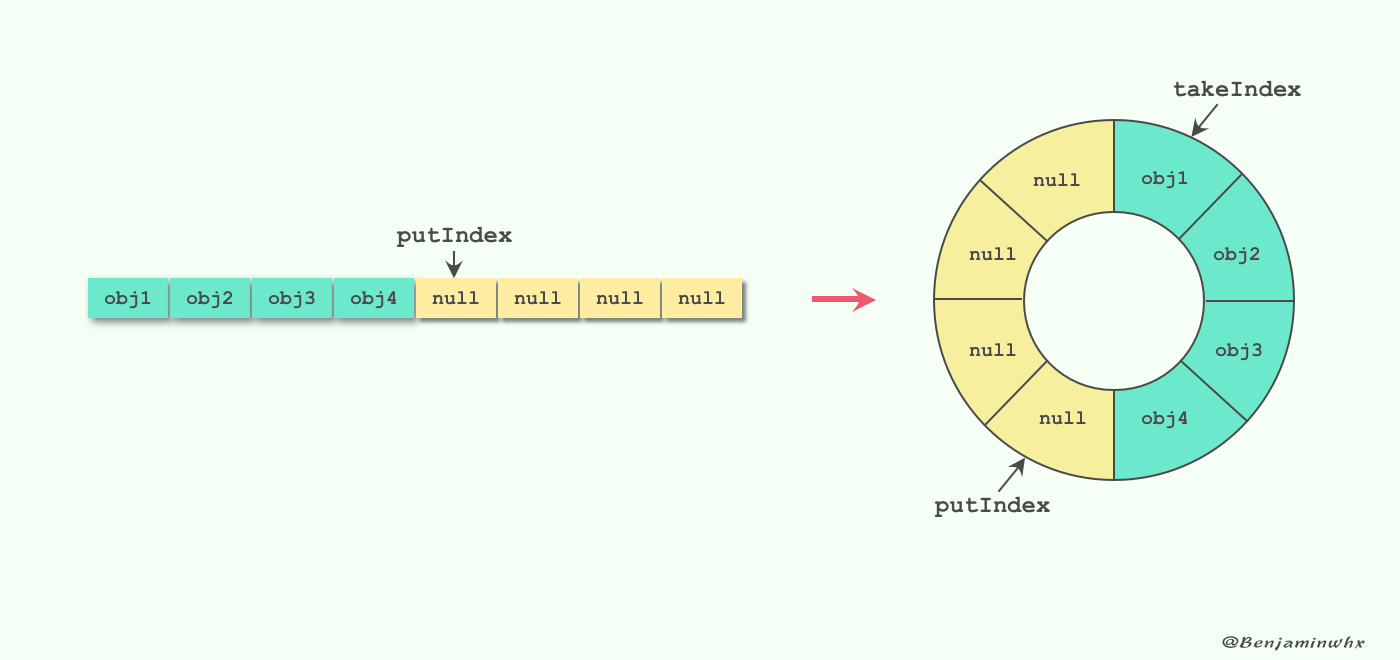
To solve this problem, we can use another logical structure to deal with the relationship between the positions in the array. Suppose we have an array A[1 n] , we can think of it as a ring structure, i.e. A[n] followed by A[1], I believe that children's shoes who have known consistency Hash algorithm should be easy to understand. As shown in the figure below: we can use two pointers to maintain the two positions of the team head and the team tail, so that the entry and exit operations can be completed in O(1) time. Of course, this ring structure is only a logical structure, and the actual physical structure is a common data.

After talking about the data structure of ArrayBlockingQueue, let's see how it implements blocking from the source level.

3. Source code analysis

3.1, attribute

//The underlying structure of the queue
final Object[] items;

//Head pointer
int takeIndex;
//Tail pointer
int putIndex;

//Number of elements in the queue
int count;

final ReentrantLock lock;

//Two states of concurrency
private final Condition notEmpty;
private final Condition notFull;

items is an array to store the data in the queue. count represents the number of elements in the queue. takeIndex and putIndex represent team head and team tail pointers respectively.

3.2. Constructor

public ArrayBlockingQueue(int capacity) {
    this(capacity, false);
}

public ArrayBlockingQueue(int capacity, boolean fair) {
    if (capacity <= 0)
        throw new IllegalArgumentException();
    this.items = new Object[capacity];
    lock = new ReentrantLock(fair);
    notEmpty = lock.newCondition();
    notFull =  lock.newCondition();
}

public ArrayBlockingQueue(int capacity, boolean fair,
                          Collection<? extends E> c) {
    this(capacity, fair);

    final ReentrantLock lock = this.lock;
    lock.lock(); // Lock only for visibility, not mutual exclusion
    try {
        int i = 0;
        try {
            for (E e : c) {
                checkNotNull(e);
                items[i++] = e;
            }
        } catch (ArrayIndexOutOfBoundsException ex) {
            throw new IllegalArgumentException();
        }
        count = i;
        putIndex = (i == capacity) ? 0 : i;
    } finally {
        lock.unlock();
    }
}

The first constructor only needs to set the queue size, which defaults to unfair lock.

The second constructor can manually specify fairness and queue size.

In the third constructor, ReentrantLock is used to lock, and then the incoming collection elements are put into items one by one. The purpose of locking here is not to use its mutex, but to make the elements in items visible to other threads (using the volatile visibility of state in AQS).

3.3, method

3.3.1 team entry method

ArrayBlockingQueue provides the implementation of various queueing operations to meet the needs of different situations. The queueing operations are as follows:

• boolean add(E e);
• void put(E e)；
• boolean offer(E e)；
• boolean offer(E e, long timeout, TimeUnit unit).

add(E e)

public boolean add(E e) {
    return super.add(e);
}

//super.add(e)
public boolean add(E e) {
    if (offer(e))
        return true;
    else
        throw new IllegalStateException("Queue full");
}

You can see that the add method calls the parent class, that is, the add method of AbstractQueue, which actually calls the offer method.

offer(E e)

Let's go to the above add method to see the offer method:

public boolean offer(E e) {
    checkNotNull(e);
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        if (count == items.length)
            return false;
        else {
            enqueue(e);
            return true;
        }
    } finally {
        lock.unlock();
    }
}

The offer method returns false when the queue is full, otherwise it calls the enqueue method to insert the element and returns true.

private void enqueue(E x) {
    final Object[] items = this.items;
    items[putIndex] = x;
    // index operation of ring
    if (++putIndex == items.length)
        putIndex = 0;
    count++;
    notEmpty.signal();
}

The enqueue method first places the element in the putIndex position of items, and then determines to set the putIndex to 0 when putIndex+1 is equal to the length of the queue, that is, the index operation of the ring mentioned above. Finally, wake up the thread waiting to get the element.

offer(E e, long timeout, TimeUnit unit)

The offer (e e e, long timeout, timeunit unit) method only adds the concept of timeout on the basis of offer (e e e).

public boolean offer(E e, long timeout, TimeUnit unit)
        throws InterruptedException {

    checkNotNull(e);
    // Convert timeout to nanoseconds
    long nanos = unit.toNanos(timeout);
    final ReentrantLock lock = this.lock;
    // Obtain an interruptible mutex
    lock.lockInterruptibly();
    try {
        // The purpose of the while loop is to prevent the incoming timeout from not being reached after the interrupt, and continue to retry
        while (count == items.length) {
            if (nanos <= 0)
                return false;
            // Wait for nanos econds, return the remaining waiting time (can be interrupted)
            nanos = notFull.awaitNanos(nanos);
        }
        enqueue(e);
        return true;
    } finally {
        lock.unlock();
    }
}

This method takes advantage of the awaitNanos method of Condition, waiting for the specified time, because the method can be interrupted, so the while loop is used to deal with the problem of remaining time after interruption. After waiting time, the enqueue method is called into the queue.

put(E e)

public void put(E e) throws InterruptedException {
    checkNotNull(e);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == items.length)
            notFull.await();
        enqueue(e);
    } finally {
        lock.unlock();
    }
}

The put method waits until it is woken up by another thread when count equals the length of items. After waking, the enqueue method is called into the queue.

3.3.2 team leaving method

After finishing the method of entering the queue, let's say the method of the queue. ArrayBlockingQueue provides the implementation of a variety of outbound operations to meet the needs of different situations, as follows:

• E poll();
• E poll(long timeout, TimeUnit unit);
• E take().

poll()

public E poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return (count == 0) ? null : dequeue();
    } finally {
        lock.unlock();
    }
}

The poll method is a non blocking method. If there is no element in the queue, null will be returned. Otherwise, dequeue will be called to get the first element out of the queue.

private E dequeue() {
    final Object[] items = this.items;
    @SuppressWarnings("unchecked")
    E x = (E) items[takeIndex];
    items[takeIndex] = null;
    if (++takeIndex == items.length)
        takeIndex = 0;
    count--;
    if (itrs != null)
        itrs.elementDequeued();
    notFull.signal();
    return x;
}

dequeue will get the element of the location according to the takeIndex, and set the location to null. Then, using the ring principle, when the takeIndex reaches the length of the list, it will set to 0, and finally wake up the thread waiting for the element to be put into the queue.

poll(long timeout, TimeUnit unit)

This method is the configurable timeout waiting method of poll(). Like the above offer, it uses the while loop + awaitNanos of Condition to wait. When the waiting time is up, execute dequeue to get the element.

public E poll(long timeout, TimeUnit unit) throws InterruptedException {
    long nanos = unit.toNanos(timeout);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == 0) {
            if (nanos <= 0)
                return null;
            nanos = notEmpty.awaitNanos(nanos);
        }
        return dequeue();
    } finally {
        lock.unlock();
    }
}

take()

public E take() throws InterruptedException {
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == 0)
            notEmpty.await();
        return dequeue();
    } finally {
        lock.unlock();
    }
}

3.3.3 method of obtaining elements

peek()

public E peek() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return itemAt(takeIndex); // null when queue is empty
    } finally {
        lock.unlock();
    }
}

final E itemAt(int i) {
    return (E) items[i];
}

The purpose of locking when getting elements here is to avoid the generation of dirty data.

3.3.4 method of deleting elements

remove(Object o)

We can imagine if we want to traverse the whole data to find an element when deleting an element in the queue, and move all elements behind the element one bit forward. That is to say, the time complexity of the method is O(n).

public boolean remove(Object o) {
    if (o == null) return false;
    final Object[] items = this.items;
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        if (count > 0) {
            final int putIndex = this.putIndex;
            int i = takeIndex;
             // From takeIndex to putIndex, until the same element as element o is found, call removeAt to delete
            do {
                if (o.equals(items[i])) {
                    removeAt(i);
                    return true;
                }
                if (++i == items.length)
                    i = 0;
            } while (i != putIndex);
        }
        return false;
    } finally {
        lock.unlock();
    }
}

The remove method is relatively simple. It traverses from takeIndex to putIndex until it finds the same element as element o and calls removeAt for deletion. Let's focus on the removeAt method.

void removeAt(final int removeIndex) {
    final Object[] items = this.items;
    if (removeIndex == takeIndex) {
        // removing front item; just advance
        items[takeIndex] = null;
        if (++takeIndex == items.length)
            takeIndex = 0;
        count--;
        if (itrs != null)
            itrs.elementDequeued();
    } else {
        // an "interior" remove

        // slide over all others up through putIndex.
        final int putIndex = this.putIndex;
        for (int i = removeIndex;;) {
            int next = i + 1;
            if (next == items.length)
                next = 0;
            if (next != putIndex) {
                items[i] = items[next];
                i = next;
            } else {
                items[i] = null;
                this.putIndex = i;
                break;
            }
        }
        count--;
        if (itrs != null)
            itrs.removedAt(removeIndex);
    }
    notFull.signal();
}

There is a little difference between the way removeAt is handled and what I think. There are two internal situations to consider

• removeIndex == takeIndex
• removeIndex != takeIndex

That is to say, when I think about it, I don't think about the boundary. When removeIndex == takeIndex, you don't need to move the later elements forward as a whole, but only need to point the takeIndex to the next element (remember that the ArrayBlockingQueue mentioned earlier can be compared to a ring).

When removeIndex! = takeindex, move the element after removeIndex forward one bit through putIndex.

4, summary

ArrayBlockingQueue is a blocking queue, in which ReentrantLock is used to realize thread safety, await and signal of Condition are used to realize the function of waiting for wakeup. Its data structure is an array. To be exact, it is a circular array (similar to a circle). All subscripts automatically start from 0 when they reach the maximum length.