A * search algorithm of Routing module

The result of Routing module is the basis of generating reference line in Planning module, which is generally referred to as global path Planning. In Routing module, the core algorithm is to generate global path through A * algorithm, besides abstracting the map as topo map for searching and generating blacklist map through KDtree. This paper mainly introduces how to use A * algorithm in topo in Routing module Search global path in map - global path.

1. Logical framework

The function of Routing module is to search a global path from the starting point to the passing point to the ending point. To complete this function, several problems need to be solved: 1) how to abstract a map into a searchable discrete map with more map information and continuous appearance; 2) how to search a * algorithm in an abstract map; 3) how to use the search results;
Let's first understand the general logic of the routing module: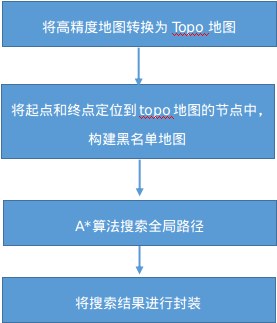

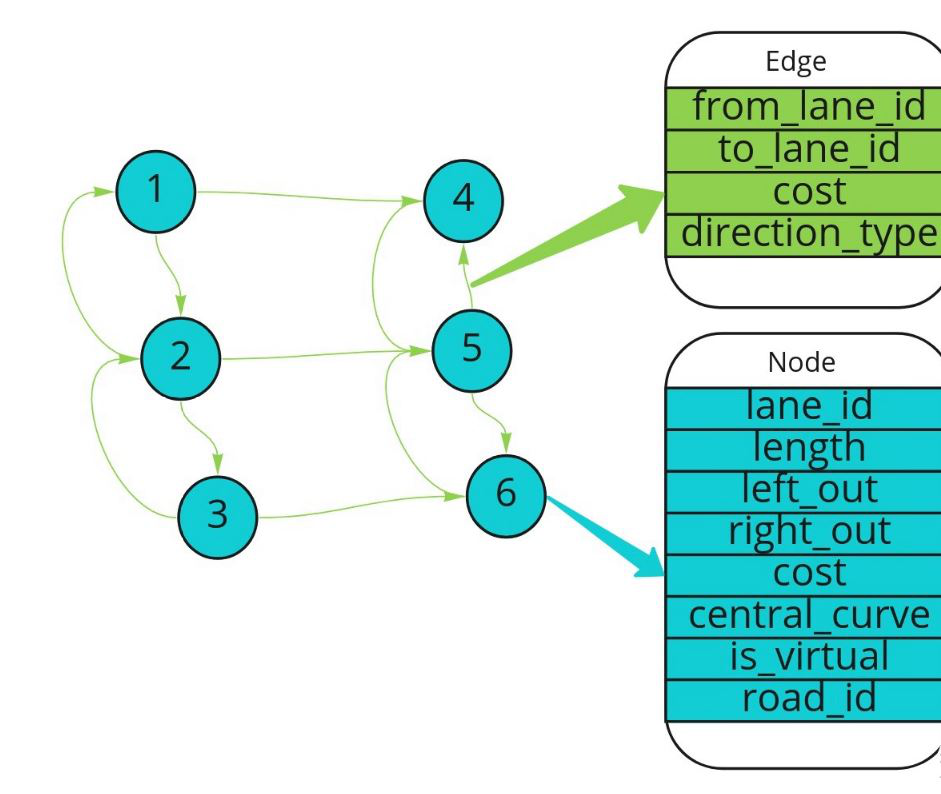
It can be seen from the above figure that routing actually transforms the high-precision map into the topo map. The topo map is composed of A series of nodes and edges. When generating nodes and edges, each node and edge will be given A certain cost. Generally, cost is related to the length of lane, turning and other attributes. Then search the topo graph by A * algorithm, and encapsulate the search results.

2.Topo map

The map information collected in high-precision map includes road, signal light, lane line, object, signal identification and many other information, which can not be directly used in the process of path search, and the main concern is the relationship between the lane and the lane. Therefore, the routing module is mainly to create nodes and edge advance through the top u creator program The result is as follows. There are many parameters defined in the map module. In the process of using, the following parameters are needed, and then A algorithm is used to search A feasible path:
The code of "routing / Topo ﹣ creator" is mainly composed of building node, building edge and building diagram. Its file structure is shown in the following figure: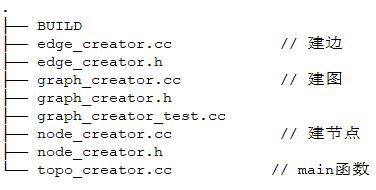

The detailed description of the nodes and graphs in the Topo graph is in the routing/graph directory, and its main information is shown in the detailed structure of the Topo map below: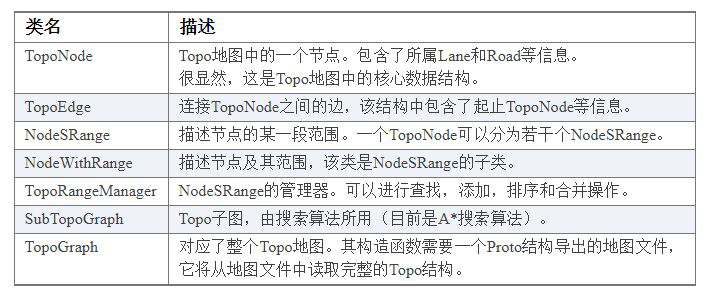

After building the topo map, search the path through algorithm A. algorithm a * is a method based on the graph search. The input of this module is the constructed graph, sub graph, starting point and target point, and the output is the route navigation information. The information of building the topo map can be understood in this way. For the road information in the figure below, it is abstracted as the information of nodes and edges in the figure below: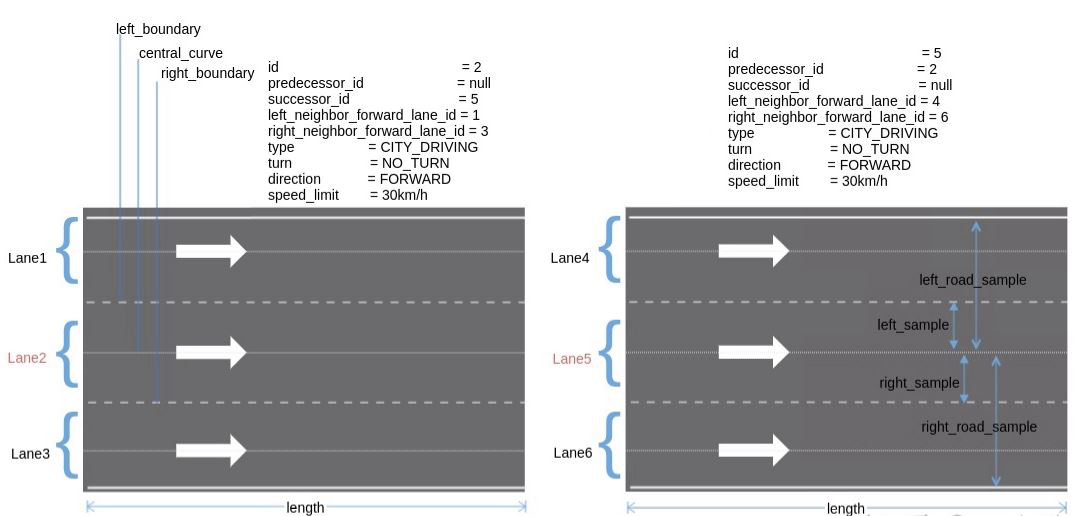

It can be seen from the figure that a road contains multiple lane information. Each lane is a search node, which also has a certain length. The front and rear lanes are connected by the predictor "ID and success" ID, and the left and right lanes are connected by the type of lane line.

3. Process of a * algorithm

1) Add the start grid to the Open List.
2) Repeat the following:
  a) Find the lattice with the lowest estimated cost F in the open list, which is called the current lattice;
  b) Switch it to the Closed List;
  c) Perform the following operations on each of the eight adjacent cells:
     i. If it cannot pass or is already in the close list, skip it; otherwise, it is as follows:;
     ii. If it is not in the open list, add it. Take the current lattice as the parent node of this lattice. Record the F, G and H values of this lattice;
     iii. if it is already in the open list, use the g value as a reference to check whether the new path is better. A lower g value means a better path. If so, change the parent node of this cell to the current cell, recalculate the G and F values of this cell, and sort the open list according to the F value again after the change.
  d) When the target cell is added to the close list, the path is found; or if the target cell is not found, the open list is empty, and the path does not exist.
3) Starting from the target cell, move along the parent node of each cell until returning to the start cell, and save the path.

The process is explained as follows: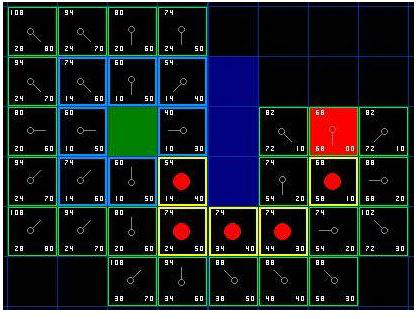

Objective: given A topo map, green is the starting position and red is the target position. The purpose of A * algorithm is to search A sequence of path points from the starting position to the target position.
Step: 1 take the current starting node as the starting point, add the adjacent points of the starting point to the open list, then calculate the cost f value of its adjacent points, then select the minimum f value, remove the minimum node from the open list, and then add it to the close list, and set its parent node as the starting node;
Step 2: set the last node as the current node. If the adjacent point of the current node is not in the open list, add it to it, calculate cost f, find the point with the lowest generation value again, remove the smallest node from the open list, add it to the close list, and set its parent node as the starting node;
Step 3, follow this until the target point is reached, and then backtrack the path to the starting point in turn according to the parent node, or the open list set to be calculated has been calculated, but not to the target point, indicating that the path search failed.

4. Application of a * algorithm in routing

The implementation process of A * algorithm in Apollo code is mainly the search() method in A star strategy.cc
The cost function is F=h+g, where g is the cost from the current node to the starting node, mainly by calculating the generation value of nodes and connected edges, and h is the heuristic function expressed by Manhattan distance:

double distance = fabs(src_point.x() - dest_point.x()) + fabs(src_point.y() - dest_point.y());

The code is interpreted as follows:

/Parameters are all graph nodes, partial graph nodes, start node, target node and result set respectively
bool AStarStrategy::Search(const TopoGraph* graph,
                           const SubTopoGraph* sub_graph,
                           const TopoNode* src_node, const TopoNode* dest_node,
                           std::vector<NodeWithRange>* const result_nodes) {
  //Clear all parameters
  Clear();
  //Log information
  AINFO << "Start A* search algorithm.";
  //std:: priority_queue is a container adapter, where the < operator is initially overloaded, so the output priority is the smallest
  //The generation value as a node that has already passed by
  std::priority_queue<SearchNode> open_set_detail;
  //Pass the source node into struct as the source SearchNode
  SearchNode src_search_node(src_node);
  //The cost value f of the source node is calculated, and the heuristic distance is Manhattan distance
  src_search_node.f = HeuristicCost(src_node, dest_node);
   // The source SearchNode is push ed into the priority queue of the pathfinding node set
  open_set_detail.push(src_search_node);
  // The source node also enters the open set
  open_set_.insert(src_node);
  // g function score, key value, calculate the mobile generation value from the source node to itself
  g_score_[src_node] = 0.0;
  // Set the S value when the source node enters, key value
  enter_s_[src_node] = src_node->StartS();
  // Define the SearchNode variable
  SearchNode current_node;
  //Define next edge set
  std::unordered_set<const TopoEdge*> next_edge_set;
  //Define sub edge set
  std::unordered_set<const TopoEdge*> sub_edge_set;
  //When the open set is not empty, check it repeatedly
  while (!open_set_detail.empty()) {
    // At this time, the node is assigned as the element at the top of the stack in the open priority, and the weight is compared with f
    current_node = open_set_detail.top();
    // Save the starting node of the current SearchNode
    const auto* from_node = current_node.topo_node;
    // If the starting node has reached the final target node, the reverse trace outputs the complete route and returns.
    if (current_node.topo_node == dest_node) {
      if (!Reconstruct(came_from_, from_node, result_nodes)) {// Is it feasible to reconstruct the path
        AERROR << "Failed to reconstruct route.";// Infeasibility indicates intermediate error
        return false;
      }
      return true;// Otherwise, it will return that the node has been found correctly
    }
    open_set_.erase(from_node);// open set node deletion
    open_set_detail.pop();// Delete the SearchNode node in the open set priority queue
     // If the count of the start node from node in the CLOSED set is not 0, it indicates that it has been checked before and is skipped directly
    if (closed_set_.count(from_node) != 0) {
      // if showed before, just skip...
      continue;
    }
    // Add start node to close set
    closed_set_.emplace(from_node);

    // if residual_s is less than FLAGS_min_length_for_lane_change, only move
    // forward
    // Get all adjacent edges of start node from node
    // If the remaining distance s from the start node to the end point is shorter than the flags min length for lane change,
    // Then the lane change is not considered, that is, only the front node is considered, and the left and right nodes are not considered. On the contrary, if s ratio
    // If the flags ﹣ min ﹣ length ﹣ for ﹣ Lane ﹣ change is long, the front and left and right nodes shall be considered.
    const auto& neighbor_edges =
        (GetResidualS(from_node) > FLAGS_min_length_for_lane_change &&
         change_lane_enabled_)
            ? from_node->OutToAllEdge()
            : from_node->OutToSucEdge();
     // Current test's mobile cost g score, initialization specifies 0
    double tentative_g_score = 0.0;
    // Get the inner contained edges from the neighbor edges, and add all the adjacent edges to the set: next edge set
    next_edge_set.clear();
    for (const auto* edge : neighbor_edges) {// For all adjacent edges
      sub_edge_set.clear();// Sub adjacent edge clearing
      sub_graph->GetSubInEdgesIntoSubGraph(edge, &sub_edge_set);// Assign sub edge set to edge
      next_edge_set.insert(sub_edge_set.begin(), sub_edge_set.end());// Import sub edge set into next edge set
    }
    // The target nodes of all adjacent edges are the adjacent nodes that we need to test one by one. We need to test the nodes one by one to find out
    // The node with the lowest total cost f = g + h is the adjacent target node required by the starting node.
    for (const auto* edge : next_edge_set) {// Loop next? Edge? Set
      const auto* to_node = edge->ToNode();
      // The adjacent node to node is in the CLOSED set, indicating that it has been checked before and is ignored directly.
      if (closed_set_.count(to_node) == 1) {
        continue;
      }
      // If the distance from the current edge to the adjacent node is less than flags min length for lane change, it means that it cannot
      // By changing the lane from the current edge to the adjacent node, it is ignored directly.
      if (GetResidualS(edge, to_node) < FLAGS_min_length_for_lane_change) { // If the distance from the edge to the node node is less than the limit value, loop again
        continue;
      }
      // Update the mobile cost value g of the current node
      tentative_g_score =
          g_score_[current_node.topo_node] + GetCostToNeighbor(edge);
      
      // If the type of edge is not forward, but left or right, indicating the situation of lane change, change the movement cost value g
      // Calculation method of.
      if (edge->Type() != TopoEdgeType::TET_FORWARD) {
        tentative_g_score -=
            (edge->FromNode()->Cost() + edge->ToNode()->Cost()) / 2;
      }

      // If the adjacent node to node is in the OPEN set and the current total cost f is greater than the moving cost g from the source node to the adjacent node, it indicates that the current situation
      // The path from the current node to the adjacent node is not optimal and is ignored directly.
      // Because the adjacent node to node is in the OPEN set, this node will be inspected later.
      if (open_set_.count(to_node) != 0 &&
          tentative_g_score >= g_score_[to_node]) {
        continue;
      }
      
      // if to_node is reached by forward, reset enter_s to start_s
      // If you arrive at an adjacent node in a forward (not left or right) way, update the access distance to node to
      // The starting distance to the node.
      if (edge->Type() == TopoEdgeType::TET_FORWARD) {
        enter_s_[to_node] = to_node->StartS();
      } else {

        // else, add enter_s with FLAGS_min_length_for_lane_change
        // If you arrive at the adjacent node to [node] left or right, update the access distance to [node] to
        // The entry distance of the current node from node plus the minimum lane change length is multiplied by the length of the adjacent node to node
        // The ratio to the length of the current node from node (the purpose of this is to normalize so that the final cost dimension is consistent).
        double to_node_enter_s =
            (enter_s_[from_node] + FLAGS_min_length_for_lane_change) /
            from_node->Length() * to_node->Length();
        // enter s could be larger than end_s but should be less than length
        to_node_enter_s = std::min(to_node_enter_s, to_node->Length());
        // if enter_s is larger than end_s and to_node is dest_node
        if (to_node_enter_s > to_node->EndS() && to_node == dest_node) { // If it is satisfied that the enter ﹐ s is larger than the end ﹐ s and the next node is the end point, the loop will be repeated again
          continue;
        }
        enter_s_[to_node] = to_node_enter_s;
      }

      // Update the cost of moving from the source point to the node (because a less expensive path has been found, it must be updated)
      g_score_[to_node] = tentative_g_score;// To node's g-score reassignment
      // Set the adjacent node to be the next node to be inspected
      SearchNode next_node(to_node);
      next_node.f = tentative_g_score + HeuristicCost(to_node, dest_node);// The f value of next'node is g score plus heuristic distance (Manhattan)
      
      // The next node to be inspected is added to the OPEN priority queue
      open_set_detail.push(next_node);

      // Set the parent of to node to from node
      came_from_[to_node] = from_node;
      // If the adjacent nodes are not in the OPEN set, they will be added to the OPEN set for further investigation
      if (open_set_.count(to_node) == 0) {// If no to node is found in the open set, add the node
        open_set_.insert(to_node);
      }
    }
  }
  // Failure to return correctly after the end of the whole cycle indicates that the search fails
  AERROR << "Failed to find goal lane with id: " << dest_node->LaneId();
  return false;
}