1 Preface
The emergence of residual network allows us to train deeper networks, but due to its multi branch reasoning, it is not as fast as plain model without residual connection. RepVGG combines three branches into one branch through the idea of heavy parameters. However, RepVGG cannot reparameterize ResNet, because the reparameterization method can only be applied to Linear Blocks, and the ReLU operation needs to be put outside. In this paper, we propose two operations (RM) of Reserving and Merging to remove residual connections based on ResBlock. Compared with ResNet and RepVGG, RMNet has better speed and accuracy, and is also friendly to high ratio pruning operation.
Thesis: https://arxiv.org/abs/2111.00687 code: https://github.com/fxmeng/RMNet
The code involved in this article has been sorted into the warehouse as a Notebook, https://github.com/MARD1NO/paper_reading/tree/master/RMNet, you can order a star for nothing
2 Introduction
We summarized the main contribution s:
- We find that re parameterization has its limitations. When nonlinear operations (such as ReLU) are placed in the residual branch, re parameterization cannot be carried out
- We propose RM method, which can remove residual connections and remove residual connections between nonlinear layers by preserving input feature mapping and merging it with output feature mapping.
- In this way, we can convert ResNet into a straight tube network, which can achieve better trade off in speed and accuracy, and is also very friendly to pruning
Supplementary materials: refer to the illustration RepVGG written before: https://zhuanlan.zhihu.com/p/352239591
3RM operation
The following figure shows how ResBlock in ResNet removes residual connections:
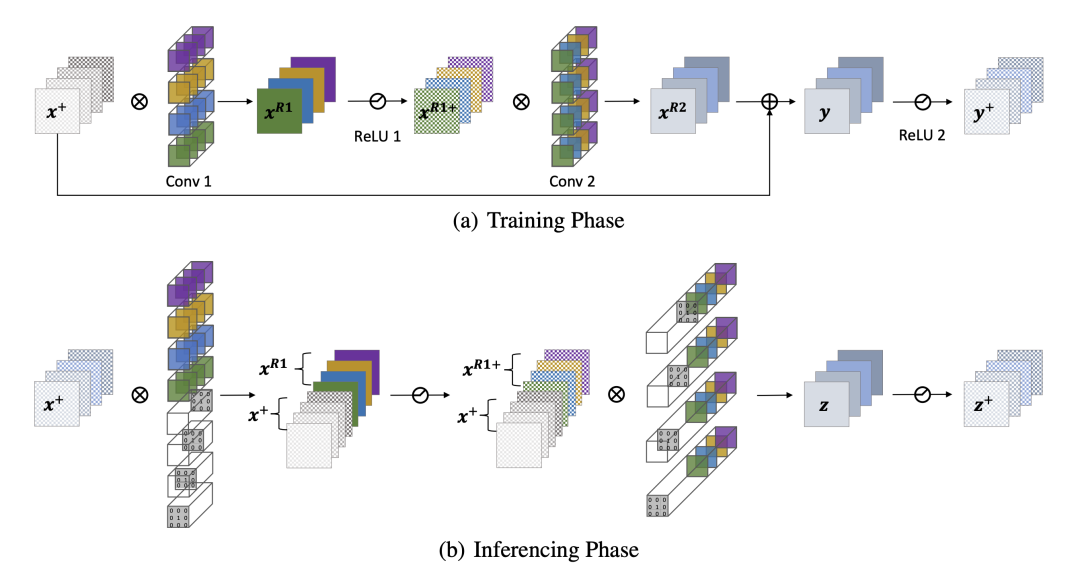
Reserving operation
Assuming that the number of input channels is 4, we insert the convolution kernel with the same number of channels and initialized by Dirac into Conv1 to Reserve the input features.
How to make convolution operate as identity mapping has been analyzed in detail in RepVGG. Here is a brief review:
If the values before and after identity remain unchanged, I will think of using a convolution kernel with a weight equal to 1 and separate channels for convolution, that is, 1x1 Depthwise convolution with a fixed weight of 1. This is equivalent to multiplying each element of each channel by 1, and then outputting it. This is the identity operation we want! The following is a schematic diagram
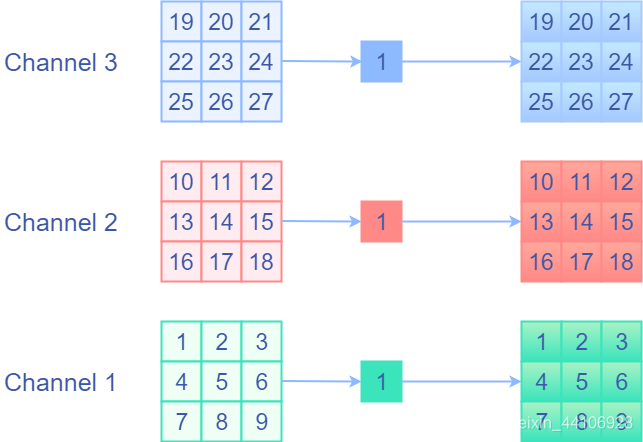
1x1Depthwise convolution equivalent
We expand to the ordinary convolution kernel, that is, set the weight of the current channel to 1 and the weight of other channels to 0. The following is a schematic diagram:
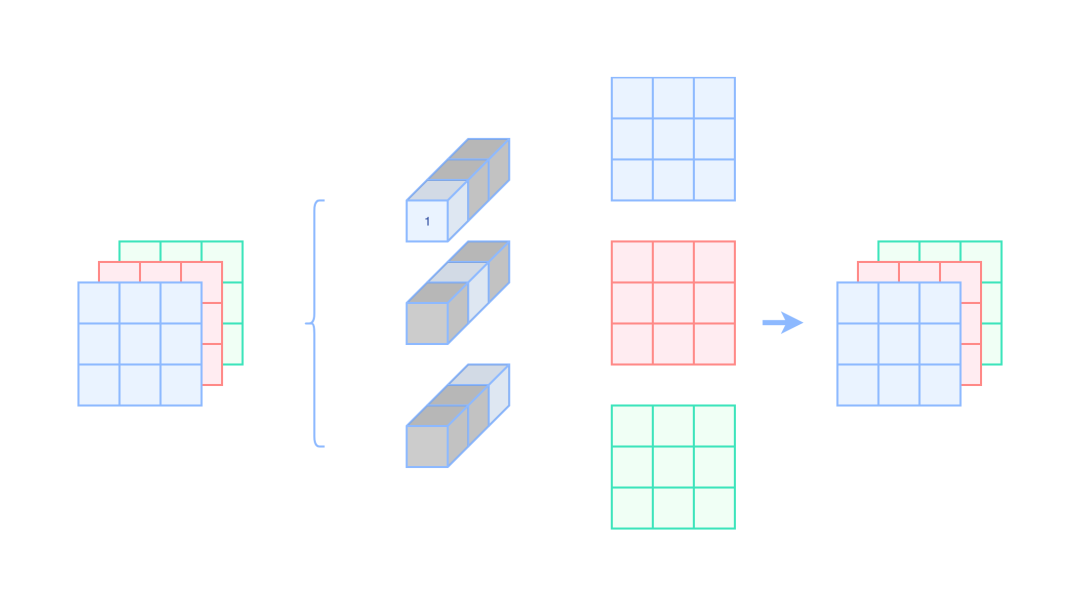
Ordinary 1x1 convolution equivalent Identity
Where the gray places indicate 0
If we want to become 3x3 convolution, we only need to circle 0 around 1x1 convolution.
In PyTorch, it is easy to initialize this convolution kernel. We only need to call nn.init.dirac_(your_weight), assuming that the number of channels is 2, the following is the example code:
import torch
import torch.nn as nn
# Outchannel, Inchannel, Kh, Kw
weight = torch.empty(2, 2, 3, 3)
nn.init.dirac_(weight)
"""
tensor([[[[0., 0., 0.],
[0., 1., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]],
[[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 1., 0.],
[0., 0., 0.]]]])
"""
For ReLU operation, there are two situations:
- For ResNet, each Block has a ReLU operation at the end. This means that every time you enter the next Block, the input must be positive. Then it is possible to directly perform the ReLU operation, as shown in the legend of the paper:

- For networks such as MobileNet2, its ReLU operation is placed in the middle of the Block. At this time, it cannot be guaranteed that the input of the next Block must be positive. Therefore, the ReLU operation cannot be performed directly at this time. Instead, a PReLU is used to set the alpha parameter of the PReLU to 1 for the input features to maintain the linear mapping. For the convoluted features, set the alpha parameter of PReLU to 0, which is equivalent to ReLU. A simple schematic diagram is as follows:
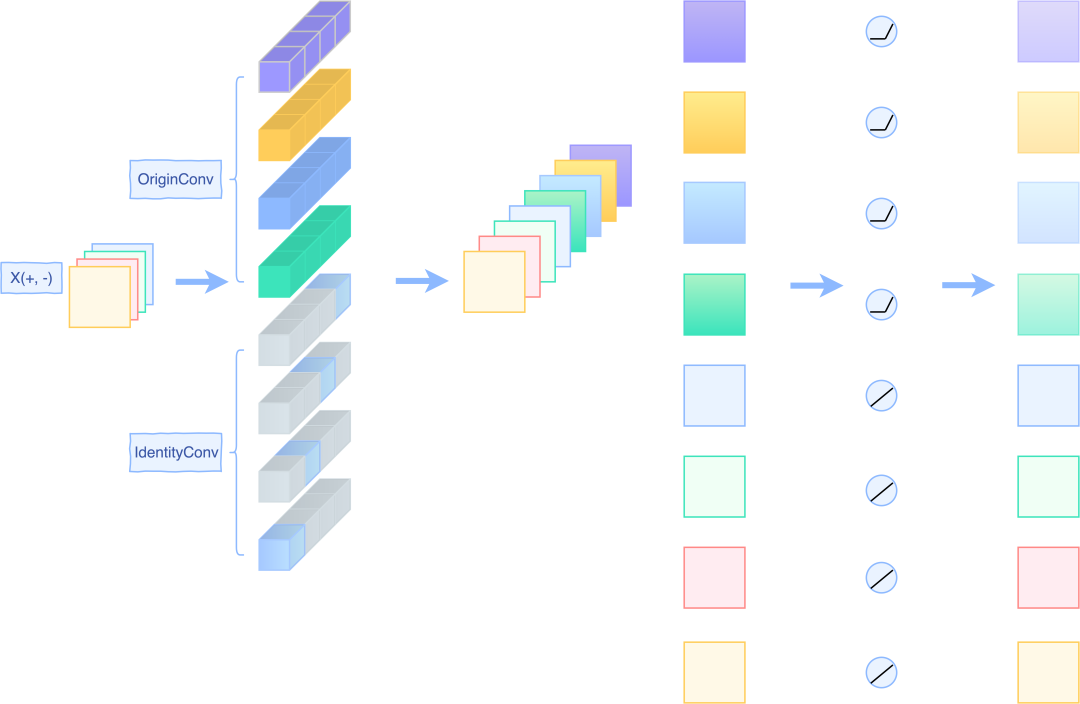
Reserve operation
Merge operation
We splice the weight initialized by Dirac to the convolution kernel for convolution, so that the residual connection can be replaced equivalently, as shown in the following figure:
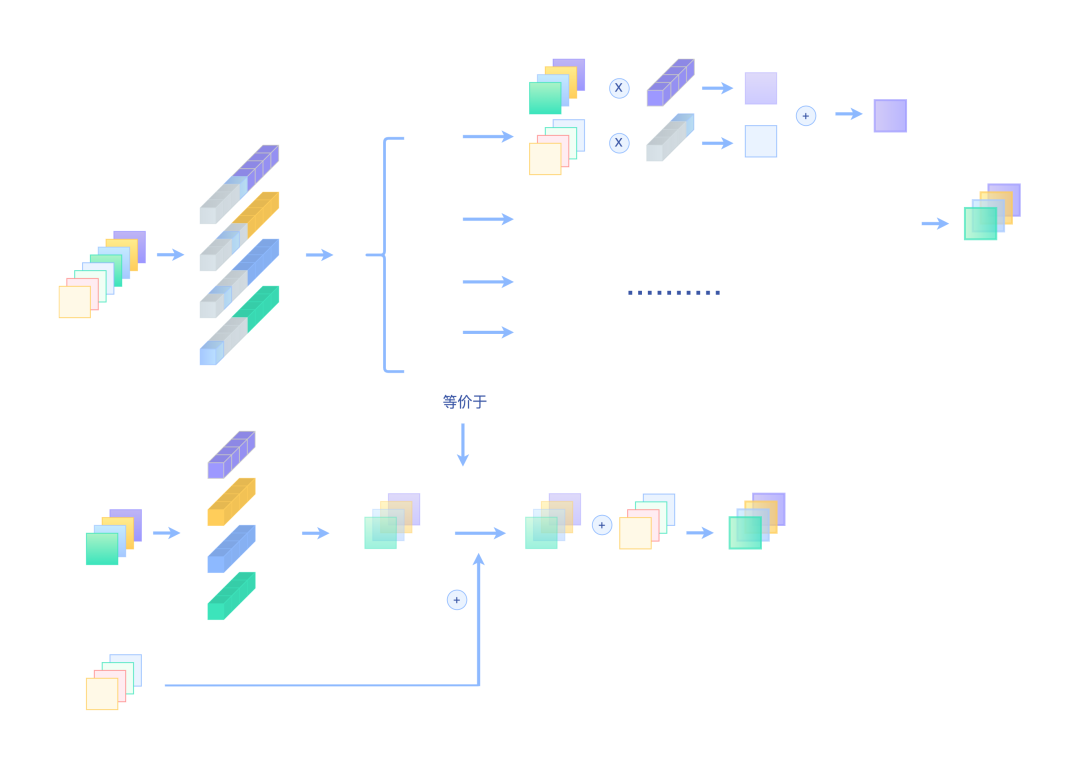
Decomposition of Merge
The upper part is the practice of RMNet, while the lower part is a residual connection operation. In addition to the illustration, we can also verify the equivalence through code
We take ResBlock as an example, and its input is a positive number
import torch
import torch.nn as nn
import numpy as np
class OriginBlock(nn.Module):
def __init__(self, planes):
super(OriginBlock, self).__init__()
self.conv1 = torch.nn.Conv2d(planes, planes, kernel_size=3, padding=1, bias=False)
self.relu1 = torch.nn.ReLU()
self.conv2 = torch.nn.Conv2d(planes, planes, kernel_size=3, padding=1, bias=False)
def forward(self, x):
y = self.conv1(x)
y = self.relu1(y)
y = self.conv2(y)
return y + x
class RMBlock(nn.Module):
def __init__(self, planes):
super(RMBlock, self).__init__()
self.mid_planes = planes * 2
self.Idenconv = torch.nn.Conv2d(planes, self.mid_planes, kernel_size=1, bias=False)
nn.init.dirac_(self.Idenconv.weight.data[:planes])
nn.init.dirac_(self.Idenconv.weight.data[planes:])
self.conv1 = torch.nn.Conv2d(self.mid_planes, self.mid_planes, kernel_size=3, padding=1, bias=False)
self.relu1 = torch.nn.ReLU()
self.conv2 = torch.nn.Conv2d(self.mid_planes, planes, kernel_size=3, padding=1, bias=False)
def forward(self, x):
y = self.Idenconv(x)
y = self.conv1(y)
y = self.relu1(y)
y = self.conv2(y)
return y
planes = 4
OriginResBlock = OriginBlock(planes)
RMResBlock = RMBlock(planes)
"""
Do some initialization
"""
# For conv1
nn.init.dirac_(RMResBlock.conv1.weight.data[:planes]) # Oc, Ic, K, K
torch.nn.init.zeros_(RMResBlock.conv1.weight.data[planes:][:, :planes])
RMResBlock.conv1.weight.data[planes:][:, planes:] = OriginResBlock.conv1.weight.data
# For conv2
nn.init.dirac_(RMResBlock.conv2.weight.data[:, :planes]) # Oc, Ic, K, K
RMResBlock.conv2.weight.data[:, planes:] = OriginResBlock.conv2.weight.data
# Insure the Input is positive.
x = torch.Tensor(np.random.uniform(low=0.0, high=1, size=(1, planes, 4, 4)))
original_res_output = OriginResBlock(x)
rmblock_output = RMResBlock(x)
print("RM output is equal?: ", np.allclose(original_res_output.detach().numpy(), rmblock_output.detach().numpy(), atol=1e-3))
Convert ResNet to VGG
Previously, we removed the residual by connecting it with the diagram and code. There is also down sampling in ResNet. A convolution with stripe = 2 will be added to the bypass branch for down sampling.
For the conversion of down sampling operation, we propose two schemes:
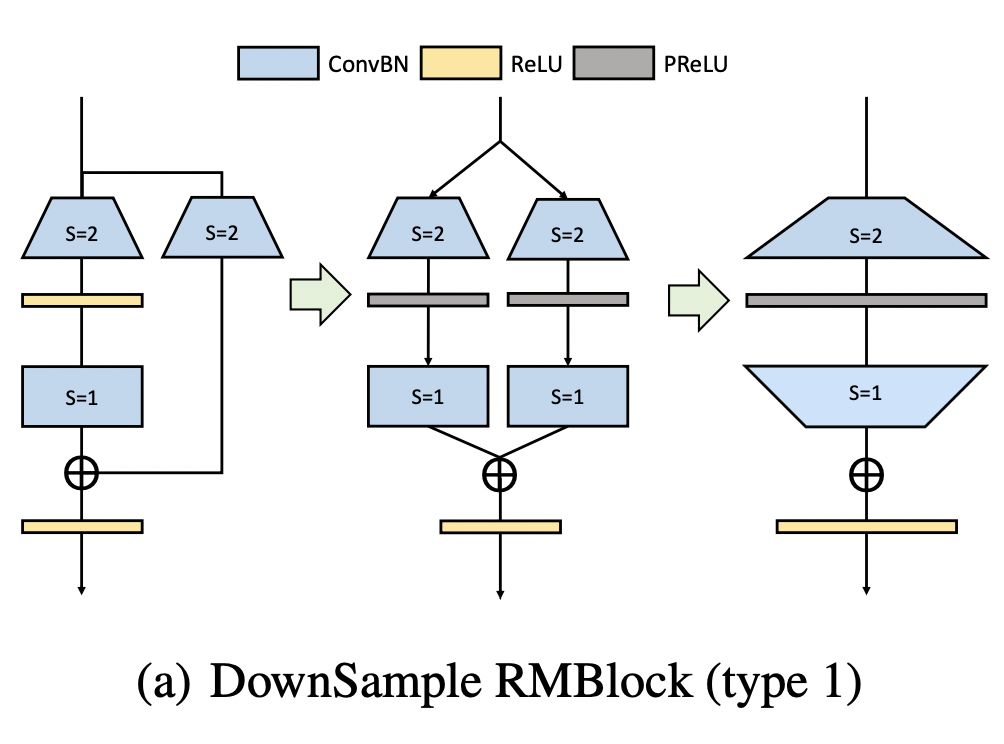
Down sampling operation V1
In the first scheme, we fill the 1x1 convolution with stripe = 2 in the bypass branch into 3x3 convolution through pad complement 0, and expand the number of channels.
At this time, the convolution results are positive and negative (similar to the case of Mobilenetv2 discussed earlier). In order to ensure the identity mapping, we use prelu (residual branch, that is, the left branch, with an alpha weight of 0, which is equivalent to ReLU, and the bypass branch with an alpha weight of 1, which is equivalent to the identity mapping).
Then we connect a Dirac initialized 3x3 convolution to ensure the identity mapping. Finally, we can merge it into the case of the rightmost figure. The corresponding codes of these three steps are as follows:
import torch
import torch.nn as nn
import numpy as np
class OriginDownSample(nn.Module):
def __init__(self, planes):
super(OriginDownSample, self).__init__()
self.conv1 = nn.Conv2d(planes, planes * 2, kernel_size=3, stride=2, padding=1, bias=False)
self.relu1 = nn.ReLU()
self.conv2 = nn.Conv2d(planes * 2, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
self.down_sample = nn.Conv2d(planes, planes * 2, kernel_size=1, stride=2, bias=False)
def forward(self, x):
y = self.conv1(x)
y = self.relu1(y)
y = self.conv2(y)
return y + self.down_sample(x)
class RMDownSampleStage1(nn.Module):
def __init__(self, planes):
super(RMDownSampleStage1, self).__init__()
self.conv1 = nn.Conv2d(planes, planes * 2, kernel_size=3, stride=2, padding=1, bias=False)
# Equals to ReLU.
self.prelu1 = nn.PReLU(planes*2)
nn.init.zeros_(self.prelu1.weight)
self.conv2 = nn.Conv2d(planes * 2, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
self.down_sample1 = nn.Conv2d(planes, planes * 2, kernel_size=3, stride=2, padding=1, bias=False)
# Linear Activation.
self.prelu2 = nn.PReLU(planes*2)
nn.init.ones_(self.prelu2.weight)
self.down_sample2 = nn.Conv2d(planes * 2, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
nn.init.dirac_(self.down_sample2.weight)
def forward(self, x):
branchA = self.conv1(x)
branchA = self.prelu1(branchA)
branchA = self.conv2(branchA)
branchB = self.down_sample1(x)
branchB = self.prelu2(branchB)
branchB = self.down_sample2(branchB)
return branchA + branchB
class RMDownSampleStage2(nn.Module):
def __init__(self, planes):
super(RMDownSampleStage2, self).__init__()
self.conv1 = nn.Conv2d(planes, planes * 4, kernel_size=3, stride=2, padding=1, bias=False)
self.prelu1 = nn.PReLU(planes*4)
self.conv2 = nn.Conv2d(planes * 4, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
def forward(self, x):
y = self.conv1(x)
y = self.prelu1(y)
y = self.conv2(y)
return y
planes = 2
OriginResDownSample = OriginDownSample(planes)
RMDownSample1 = RMDownSampleStage1(planes)
RMDownSample2 = RMDownSampleStage2(planes)
"""
Do Some Initialization
"""
RMDownSample1.conv1.weight = OriginResDownSample.conv1.weight
RMDownSample1.conv2.weight = OriginResDownSample.conv2.weight
# Padding from zero value to convert 1x1 to 3x3 kernel
RMDownSample1.down_sample1.weight = torch.nn.Parameter(
torch.nn.functional.pad(
OriginResDownSample.down_sample.weight.data, [1, 1, 1, 1], value=0.0)
)
x = torch.Tensor(np.random.uniform(low=0.0, high=1, size=(1, planes, 4, 4)))
original_res_output = OriginResDownSample(x)
rmblock_output = RMDownSample1(x)
print("RM output is equal?: ", np.allclose(original_res_output.detach().numpy(),
rmblock_output.detach().numpy(),
atol=1e-4))
RMDownSample2.conv1.weight = torch.nn.Parameter(
torch.cat(
[RMDownSample1.conv1.weight, RMDownSample1.down_sample1.weight], dim=0)
)
RMDownSample2.prelu1.weight = torch.nn.Parameter(
torch.cat(
[RMDownSample1.prelu1.weight, RMDownSample1.prelu2.weight], dim=0)
)
RMDownSample2.conv2.weight = torch.nn.Parameter(
torch.cat(
[RMDownSample1.conv2.weight, RMDownSample1.down_sample2.weight], dim=1)
)
rmblock_outputv2 = RMDownSample2(x)
print("RM output is equal?: ", np.allclose(rmblock_outputv2.detach().numpy(),
rmblock_output.detach().numpy(),
atol=1e-4))
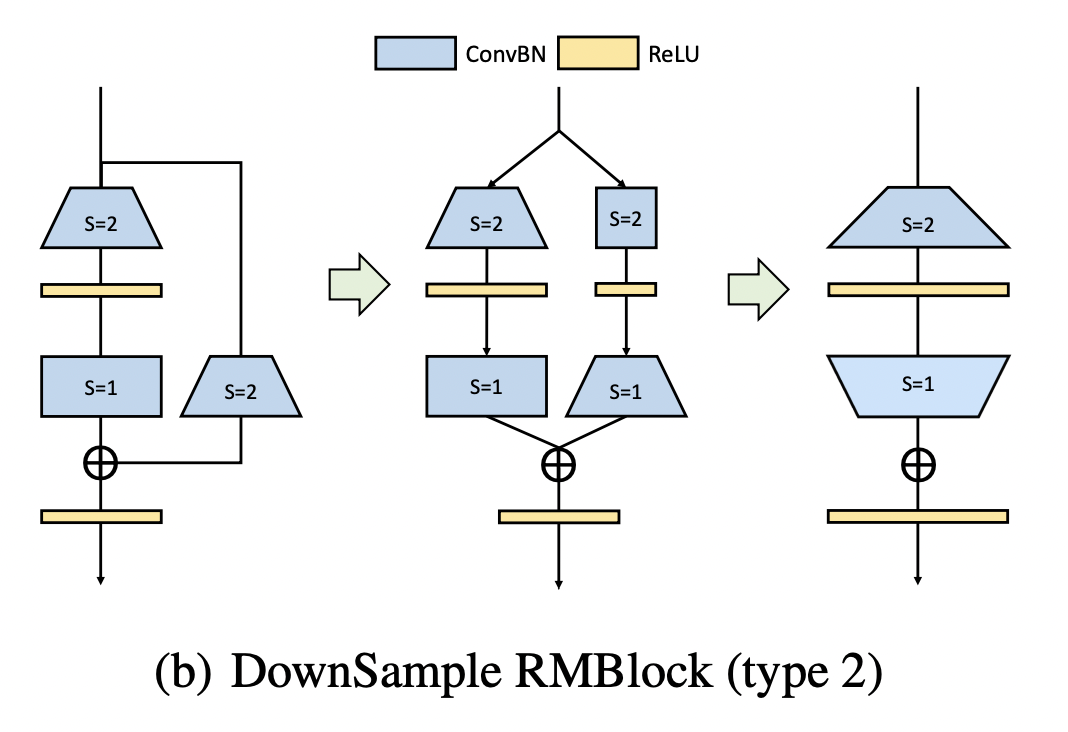
Down sampling operation V2
In the second scheme, the identity mapping convolution with size 3x3 and stripe = 2 is used to reduce the resolution. Then expand the number of channels by 3x3 convolution with stripe = 1, corresponding code:
import torch
import torch.nn as nn
import numpy as np
class OriginDownSample(nn.Module):
def __init__(self, planes):
super(OriginDownSample, self).__init__()
self.conv1 = nn.Conv2d(planes, planes * 2, kernel_size=3, stride=2, padding=1, bias=False)
self.relu1 = nn.ReLU()
self.conv2 = nn.Conv2d(planes * 2, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
self.down_sample = nn.Conv2d(planes, planes * 2, kernel_size=1, stride=2, bias=False)
def forward(self, x):
y = self.conv1(x)
y = self.relu1(y)
y = self.conv2(y)
return y + self.down_sample(x)
class RMDownSampleV2Stage1(nn.Module):
def __init__(self, planes):
super(RMDownSampleV2Stage1, self).__init__()
self.conv1 = nn.Conv2d(planes, planes * 2, kernel_size=3, stride=2, padding=1, bias=False)
self.relu1 = nn.ReLU()
self.conv2 = nn.Conv2d(planes * 2, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
self.identity_down_sample = nn.Conv2d(planes, planes, kernel_size=3, stride=2, padding=1, bias=False)
nn.init.dirac_(self.identity_down_sample.weight)
self.relu2 = nn.ReLU()
self.down_sample2 = nn.Conv2d(planes, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
def forward(self, x):
branchA = self.conv1(x)
branchA = self.relu1(branchA)
branchA = self.conv2(branchA)
branchB = self.identity_down_sample(x)
branchB = self.relu2(branchB)
branchB = self.down_sample2(branchB)
return branchA + branchB
class RMDownSampleV2Stage2(nn.Module):
def __init__(self, planes):
super(RMDownSampleV2Stage2, self).__init__()
self.conv1 = nn.Conv2d(planes, planes * 3, kernel_size=3, stride=2, padding=1, bias=False)
self.relu1 = nn.ReLU()
self.conv2 = nn.Conv2d(planes * 3, planes * 2, kernel_size=3, stride=1, padding=1, bias=False)
def forward(self, x):
y = self.conv1(x)
y = self.relu1(y)
y = self.conv2(y)
return y
planes = 2
OriginResDownSample = OriginDownSample(planes)
RMDownSample1 = RMDownSampleV2Stage1(planes)
RMDownSample2 = RMDownSampleV2Stage2(planes)
"""
Do Some Initialization
"""
RMDownSample1.conv1.weight = OriginResDownSample.conv1.weight
RMDownSample1.conv2.weight = OriginResDownSample.conv2.weight
# Padding from zero value to convert 1x1 to 3x3 kernel
RMDownSample1.down_sample2.weight = torch.nn.Parameter(
torch.nn.functional.pad(
OriginResDownSample.down_sample.weight.data, [1, 1, 1, 1], value=0.0)
)
x = torch.Tensor(np.random.uniform(low=0.0, high=1, size=(1, planes, 4, 4)))
original_res_output = OriginResDownSample(x)
rmblock_output = RMDownSample1(x)
print("RM output is equal?: ", np.allclose(original_res_output.detach().numpy(),
rmblock_output.detach().numpy(),
atol=1e-4))
RMDownSample2.conv1.weight = torch.nn.Parameter(
torch.cat(
[RMDownSample1.conv1.weight, RMDownSample1.identity_down_sample.weight], dim=0)
)
RMDownSample2.conv2.weight = torch.nn.Parameter(
torch.cat(
[RMDownSample1.conv2.weight, RMDownSample1.down_sample2.weight], dim=1)
)
rmblock_outputv2 = RMDownSample2(x)
print("RM output is equal?: ", np.allclose(rmblock_output.detach().numpy(),
rmblock_outputv2.detach().numpy(),
atol=1e-4))
The parameters of the two schemes are
- Scheme 1: Conv1(C*4C*3*3) + PReLU(4C) + Conv2(4C*2C*3*3) = 108C^2 + 4C
- Scheme 2: Conv1(C*3C*3*3) + Conv2(3C*2C*3*3) = 81C^2
The parameter quantity of scheme 2 is only 75% of scheme 1, so we choose scheme 2
Convert MobileNetV2 to MobileNetV1
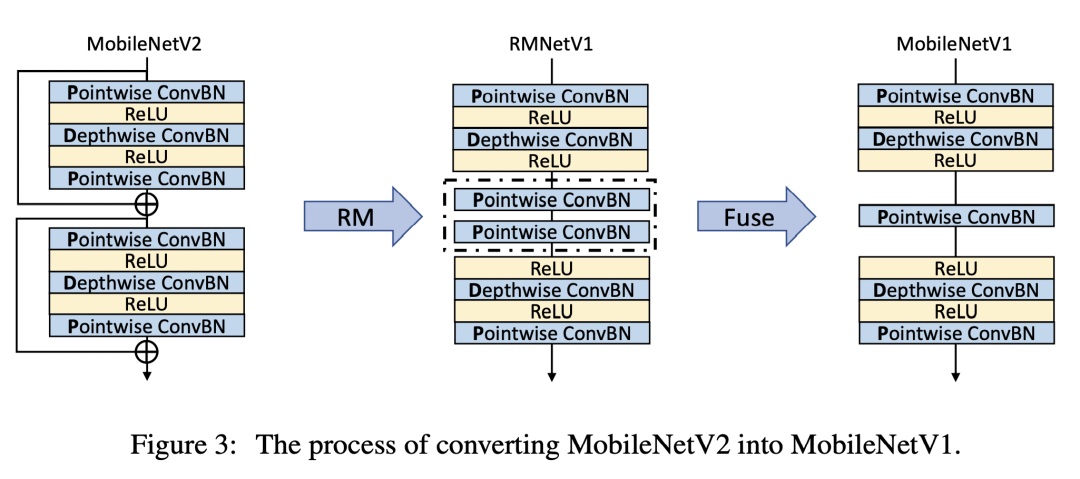
Convert to MobileNetV1
This part of the idea is similar to the previous one. The author only briefly describes it here. Firstly, the residual branch is removed by RM operation. Then the two convolution layers in the middle can be fused into one convolution layer, and the corresponding formula is as follows:
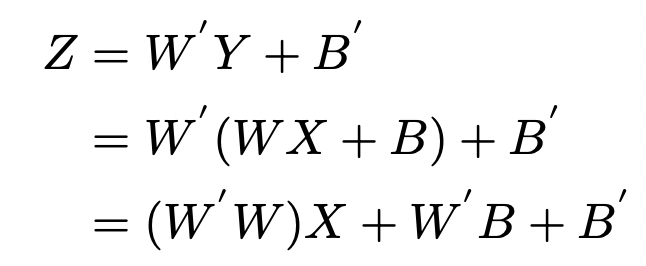
Fusion convolution formula
prune
After removing the residual operation, we are also very friendly to pruning. RMNet can prune in a higher proportion:
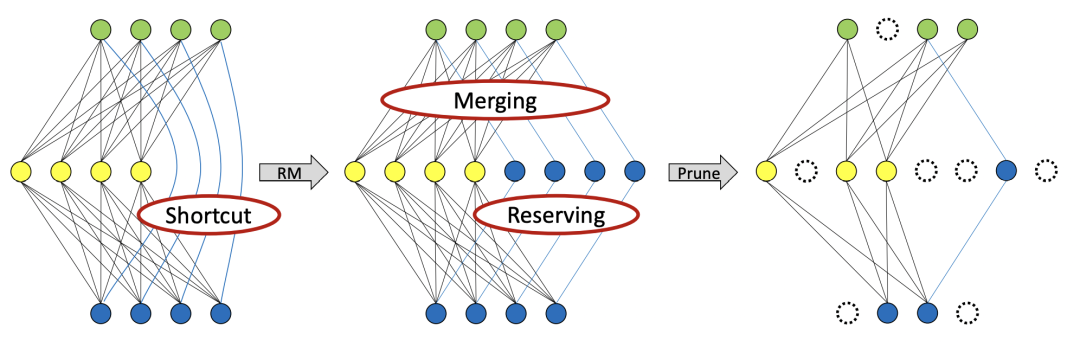
4 Experiment
In the experimental part, the author also briefly introduces it. Interested readers can read the original text.
Firstly, the author shows the results of RepVGG and RMNet in the case of depth deepening. Because RepVGG has no cross layer residual connection, the accuracy decreases when the network deepens, while the accuracy of RMNet is always online:
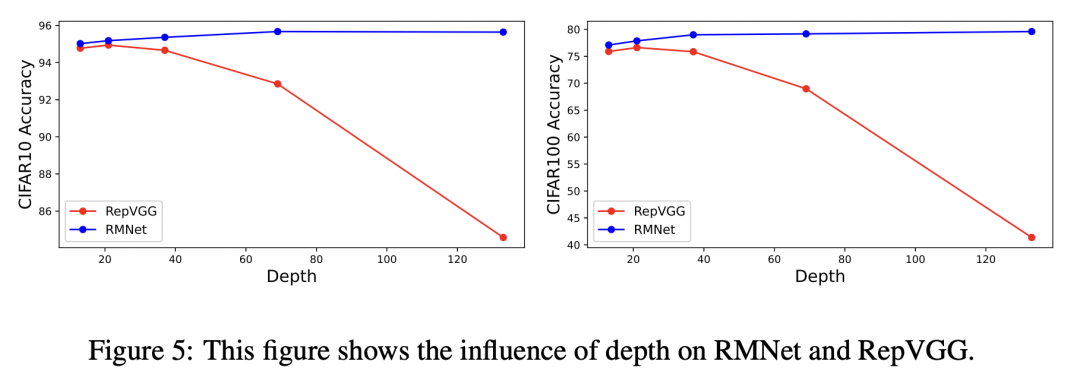
Impact of network deepening
By setting the number of packet convolution channels and appropriate expansion width, RMNet can also achieve a good Trade-off in accuracy and speed. Including RMNet 50x6_32 represents a depth of 50 layers, 6 represents a width ratio, and 32 represents the number of convolution channels per packet. Under the same experimental conditions as RepVGG:
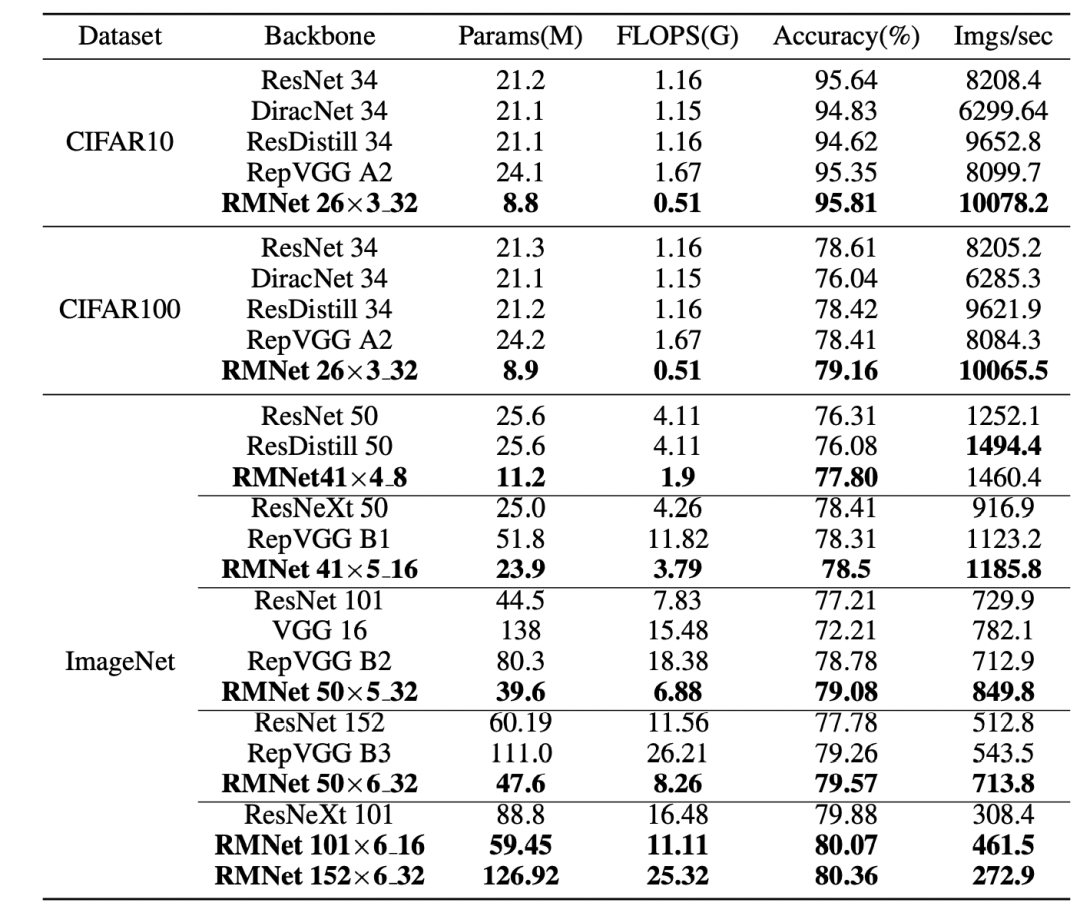
Comparison of data sets
Finally, a Pruning Experiment:
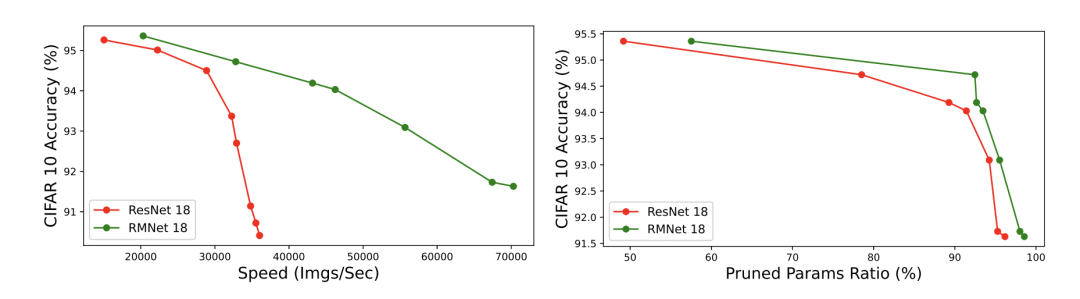
Pruning Experiment
5 Conclusion
In my opinion, this is a sincere work. The RM operation proposed by the author, developed in the original heavy parameter idea, removes the residual connection that people love and hate. Although this operation will double the number of network channels, a high ratio pruning operation can be applied to make up for this defect. I highly recommend you to read the code ~