A case study of common numpy methods for Python data analysis
Statement and introduction
numpy is the basic package of python data scientific computing. This package includes multidimensional data object ndarray and many of its derived objects (such as mask array and matrix). At the same time, these objects also provide common scientific computing methods such as mathematics, logic, shape processing, sorting, selection, discrete Fourier transform, basic linear algebra, basic statistical operation, random simulation and so on.
Create ndarray
Create ndarray directly
#Create an array of ndarray directly through np.array. import numpy as np arr1=np.array([4,6,9]) print(type(arr1[2],arr1) #It is not difficult to see that the type of element here is int <class 'numpy.int32'> [4 6 9]
Type conversion
This code is by Java Architect must see network-Architecture sorting #1. The data types defined in ndarry are generally unified. If they are not unified, they can be converted automatically when the types can be converted. For example, int to float import numpy as np arr1=np.array([4.32,6,9]) print(type(arr1[2],arr1) #It is not difficult to see that the type of the element here is converted to float <class 'numpy.float64'> [4.32 6. 9. ] # 2 float to str import numpy as np arr1=np.array([4.32,'we',9]) print(type(arr1[2],arr1) #result <class 'numpy.str_'>
Create from template
All elements are 0
#ndarray can be initialized through np.zeros and np.ones to specify the size and type. #Create a one-dimensional ndarray with three elements of 0. arr1=np.zeros(3,dtype=float)
All elements are 1
This code is by Java Architect must see network-Architecture sorting #Create an array with 3 rows and 4 columns and all 1 elements. arr1=np.ones((3,4),dtype=int)
Specific element
# Create an array with 2 rows and 3 columns and all elements of 5.12. arr1=np.full((2,3),5.12)
Equal difference array step method
Can pass numpy of arange Method to generate equal difference ndarray,Specify the start value, end value, step size (increment). For example, generate an equal difference array starting with 1, increasing by 3 each time, and taking 20 as the final value. Note: it's less than 20 here. print(np.arange(1,20,3)) #The result is: [ 1 4 7 10 13 16 19] #Of course, the increase here can be negative, that is print(np.arange(20,1,-3)) #The result is [20 17 14 11 8 5]
Bisection array average method
#You can divide the array equally by the starting value and the number of copies, such as generating three equal difference elements from 3 to 15. print(np.linspace(3,15,3)) #As a result, the calculation method is (15-3) / 3, so the step size is 6. [ 3. 9. 15.]
Uniformly distributed random number
#Random numbers can be generated through the np.random module. Here, call its random method to generate uniform random numbers. Uniform distribution, that is, the points in the specified interval have the same probability to be taken. For example: generate 2×2 Array whose elements are uniform random numbers between 0 and 1. print(np.random.random((2,2))) #result [[0.15185125 0.52790783] [0.16011147 0.29797948]]
Normal distribution random number
#Random numbers can be generated through np.random module. Here, call its normal method to generate random numbers with positive distribution. Where the standard normal distribution is 0 of the mean and the standard deviation is 1. print(np.random.normal(0,1,(2,2))) #result [[-0.25384836 -2.06285573] [-2.27651345 0.90667998]]
Random integer
# 1 random numbers can be generated through the np.random module. Here, call its random method to generate random numbers of the specified type. #Generate 6 random numbers between 2 and 20 print(np.random.randint(2,20,6)) #As a result, of course, you can also specify an array of other shape s. [ 9 3 12 11 10 12]
Generate main diagonal array
adopt np.eye Diagonal arrays (matrices) can be generated. print(np.eye(4)) #result [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
data type
Detailed explanation of data types
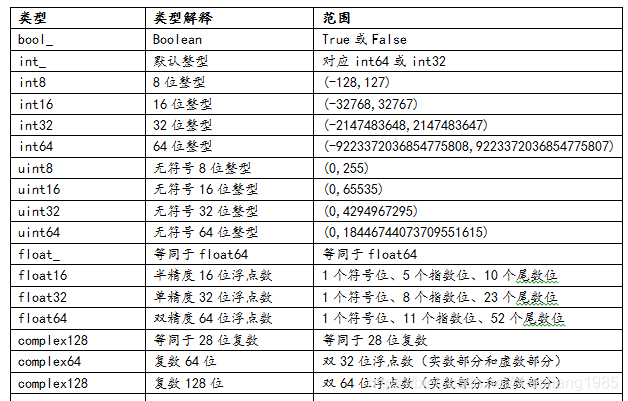
Note: you can view the range of a type (including minimum and maximum values) through numpy Built in methods, such as viewing float16 The maximum value of can be: print(np.finfo(np.float16)) #result Machine parameters for float16 --------------------------------------------------------------- precision = 3 resolution = 1.00040e-03 machep = -10 eps = 9.76562e-04 negep = -11 epsneg = 4.88281e-04 minexp = -14 tiny = 6.10352e-05 maxexp = 16 max = 6.55040e+04 nexp = 5 min = -max But for float16,We can only define up to 65519.0,But the output value is 65500.0,And defined as 65520.0 Is displayed as inf(Infinite integer).
Basic method of ndarray
Dimension ndim
Dimensions are similar to our perspective of looking at things in space. Common ones include 1-dimensional straight line, 2-dimensional plane, 3-dimensional solid, higher dimension, etc. The ndim method is used in np to view dimensions.
print(np.random.randint(1,20,(2,4,5)).ndim) #The result is that the array is 3-dimensional. 3 #It's better to multiply length by width by height.
shape
The shape shape is the size of each shape and returns a tuple. It is obviously (2,4,5) here. Generally, we say it is 2 × four × 5.
print(np.random.randint(1,20,(2,4,5)).shape) #result (2, 4, 5)
Size size
The size statistics is the number of elements in the whole array. Here, it is not difficult to know that the above array has a total of 2 * 4 * 5 = 40 elements.
print(np.random.randint(1,20,(2,4,5)).size) #result 40
Data type dtype
The data type is the type of elements in the current array, such as int and float.
print(np.random.randint(1,20,(2,4,5)).dtype) #result int32
Accessing array elements
# 1 elements can be accessed through the array index (in the form of brackets and subscripts). For example, you can access elements that intersect the first, second and third dimensions in the following ways. Note that the array index starts at 0. arr4=np.random.randint(1,20,(2,4,5)) print(arr4,arr4[0][1][2]) #perhaps print(arr4,arr4[0,1,2]) #The results were random. 15 # 2. You can use the index values: - 1, - 2..., if you want to retrieve in reverse. For example, if you want to get element 8, the reverse corresponding index value is - 2. print(np.array([2,8,9])[-2]) #result 8
Normal array slice
You can access the array by specifying the index range, that is, the slice form. #For example, when accessing the first four elements of a 1-dimensional array, note that because python follows the principle of closing left and opening right, the rightmost value cannot be obtained. That is, the indexes are 0, 1, 2 and 3, excluding 4. print(np.array([2,8,9,10,23,27])[:4]) #result [ 2 8 9 10] #For example, access the 2nd to 4th elements of a 1-dimensional array. The principle is the same as above. print(np.array([2,8,9,10,23,27])[2:4]) #result [ 9 10] #3 index from one position to the last print(np.array([2,8,9,10,23,27])[4:]) #result [23 27] #4 take it from the back to the front, such as - 3 to - 1. Here, it is also closed on the left and open on the right, that is, - 1 cannot be taken. print(np.array([2,8,9,10,23,27])[-3:-1]) #result [10 23]
Skip array slice
#1 index is taken every other bit, for example, starting from 0, an element is taken every 2 index numbers print(np.array([2,8,9,10,23,27])[::2]) #result [ 2 9 23] #2 index spacing specifies the starting index position. For example, the index starts from 3 and takes an element every 2 index numbers. print(np.array([2,8,9,10,23,27])[3::2]) #result [ 2 9 23] #3 element reversal, that is, the output array and the original array elements are reverse. print(np.array([2,8,9,10,23,27])[::-1]) #result [27 23 10 9 8 2] #4 specify the index value reversal elements, that is, the output array is the original array elements in reverse order from the specified index position. The number of elements is the specified value + 1. For example, the output array here should be 4 + 1 = 5 elements. print(np.array([2,8,9,10,23,27])[4::-1]) #result [23 10 9 8 2] Note: the data slice of high-dimensional data is similar.
Shape conversion
Here is by calling reshape Method converts an array into a shape. For example, convert a 1-dimensional array to 2, 2×3 Array of. print(np.array([2,8,9,10,23,27]).reshape(2,3)) #result [[ 2 8 9] [10 23 27]]
merge
# 1. When arrays of the same dimension are merged, np concatenate can be merged, and the original dimension will not be changed after merging. x=np.array([1,2,3,4]) y=np.array([6,7,8]) print(np.concatenate([x,y])) #result [1 2 3 4 6 7 8] Note: multiple arrays can be merged, not necessarily 2. #2. When merging different dimensions (generally one dimension is missing), you need to specify the direction, such as by column (np.vstack) and row (np.hstack) here vstack of v Corresponding word vertical That is, vertical (keep the column direction consistent) hstack of h Corresponding word horizontal I.e. horizontal (keep the row direction consistent) #2.1 vstack vertical merge x=np.array([1,2,3]) y=np.array([[6,7,8],[9,5,10]]) print(np.vstack([x,y])) #As a result, it can be seen that the number of columns is equal, that is, there are three. [[ 1 2 3] [ 6 7 8] [ 9 5 10]] #2.2 hstack horizontal merge x=np.array([[1,2,3],[4,5,6]]) y=np.array([[6,7,8],[9,5,10]]) print(np.hstack([x,y])) #2.2 dstack merge to generate new dimension x=np.array([[1,2,3],[3,2,1]]) y=np.array([[6,7,8],[9,5,10]]) print(np.dstack([x,y])) #result [[[ 1 6] [ 2 7] [ 3 8]] [[ 3 9] [ 2 5] [ 1 10]]]
split
Splitting and merging are the opposite operations. # 1 specify the split middle section, and the rest takes the head and tail of the section. x=np.array([1,2,3,4,5,6]) x1,x2,x3=np.split(x,[2,5]) print (x1,x2,x3) #2 vsplit vertical segmentation, keeping the number of columns unchanged. The number of splits N here is 1 less than the subarray, that is, the subarray is N+1. x=np.array([[1,2,3,4],[5,6,7,8]]) x1,x2=np.vsplit(x,[1]) print (x1,x2) #result [[1 2 3 4]] [[5 6 7 8]] #3 hsplit vertical segmentation, keeping the number of columns unchanged. The split parameter N here refers to the index position. The meeting is divided into two parts. x=np.array([[1,2,3,4],[5,6,7,8]]) x1,x2,x3=np.hsplit(x,[3]) print (x1,x2,x3) #result [[1 2 3] [5 6 7]] [[4] [8]] #4 hsplit vertical segmentation, keeping the number of columns unchanged. If the split parameter here can be a section, it will be divided into three parts. x=np.array([[1,2,3,4],[5,6,7,8]]) x1,x2,x3=np.hsplit(x,[2,3]) print (x1,x2,x3) #result [[1 2][5 6]] [[3] [7]] [[4] [8]]