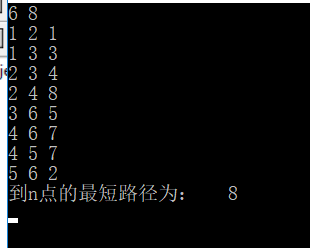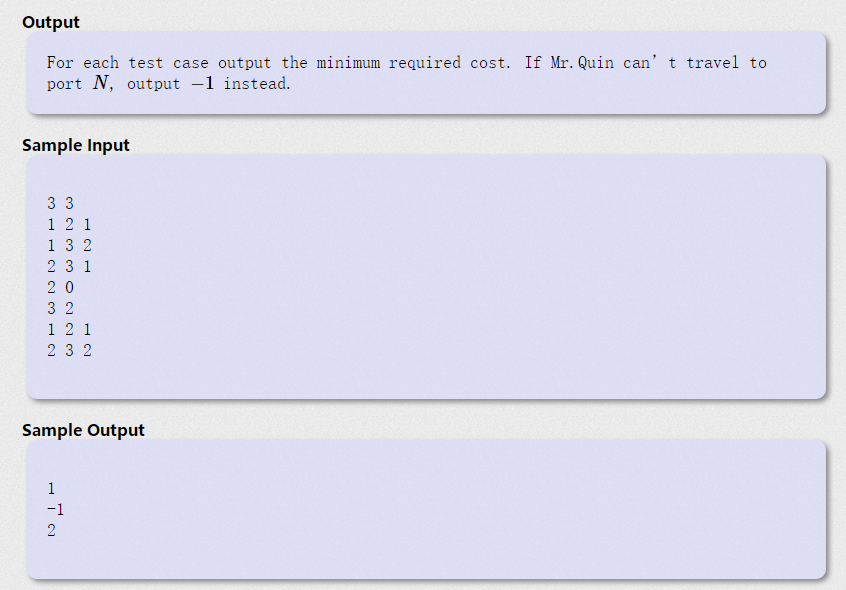
To solve this problem, dfs+bfs can be used, but I will not, so I will only dijkstra algorithm;
In order to solve this problem, we must understand the core idea of Dijstela's algorithm, as I understand it:
I can give any example of a graph: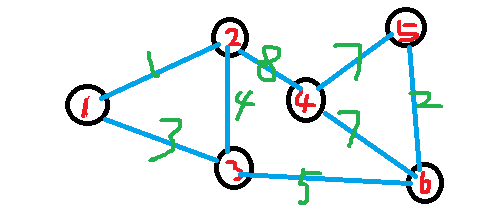
For example, in this graph, find the shortest path of 1 - 6; of course, this point is seldom stored in a two-dimensional array;
Dijkstra thought: I first use the dis [] array to save the distance of all points that 1 can reach, and then set the other points to INF (usually INF to 0x3f3f3f3f3f is enough);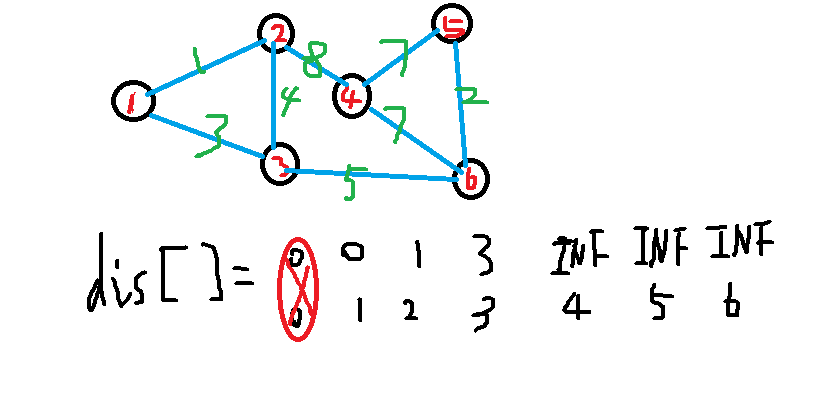
Then I can use the available points as transit stations and find other points that can be reached, and then update the dis array value each time.
For example, we start at 2 o'clock and enumerate all the points that 2 can reach (of course, since 1 has already been found, we should mark it with an array book[1]=1 that it has already passed);
Then 2 can only reach 4 and 3, then compare the distance from 1 to 4 (INF) and the distance from 1 to 2 to 4 (1 + 8), because less than INF, dis[4] is updated to 9;
The same is true for Reactor 3, which is marked every time it passes through the transit station, because it is impossible to walk repeatedly.
So the question arises, how to think about this idea?
First of all, I should make it clear that all points except the first point will be used as transit stations, so the large for cycle is 1-n-1 points. Note: here the large for is only used to indicate that each point needs to be used as a transit station; and there is no necessary logical connection with the content inside;
So the simplest Dijkstra algorithm comes out (because this algorithm does not consider the case of too large arrays):
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
int Map[1000][1000],n,m;//Map is used to record the path value from point a to point b. n denotes how many points are there and m denotes how many edges are given.
int dis[1000],book[1000];//dis is used to indicate the distance from the start point to other points, and book is used to mark whether the loop to this point has been marked.
void dijkstra(int start){//The simplest dijkstra algorithm (in matrix form)
//First, find the distance between this point and other points using a for
int Min=INF;
for(int i=1;i<=n;i++){//Initialize all distances from the start point to the point reachable to the start point
dis[i]=Map[start][i];//Note that dis and Map are only logically related here
}
//Here we need to enumerate n-1 points, because the starting point does not need to be calculated.
//So use a big for loop.
book[start]=1;//The marking start point has been used as a transit point.
for(int i=1;i<=n-1;i++){
//Find the first shortest point to start
//And the marker has been selected.
Min=INF;
int u;//Record the shortest point of start
for(int j=1;j<=n;j++){
if(book[j]==0&&dis[j]<Min){//Search for the smallest distance from a point that has a direct edge to start // Here's the best way to think about undirected graphs
Min=dis[j];
u=j;
}
}
book[u]=1;//The point u has been used as a transit station.
//Then find the distance from the other point of the u-point to the start and the distance through the point of u, and compare the size.
for(int e=1;e<=n;e++){//Here e is the abbreviation of end. It is easy to understand that u is another point that can be reached as a transit station.
if(Map[u][e]<INF){
if(dis[e]>dis[u]+Map[u][e]){//This is the comparison of the above analysis.
dis[e]=dis[u]+Map[u][e];
}
}
}
}
}
void init(int n){
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++){
if(i==j) Map[i][j]=0;//To be oneself is 0.
else Map[i][j]=INF;//Others are set to INF
}
}
}
void read(int m)//This is used for input, because functions are written separately to better understand their functions.
{
int a,b,c;
for(int i=1;i<=m;i++){
cin>>a>>b>>c;
Map[a][b]=c;//Let it be undirected graph
Map[b][a]=c;
}
}
int main(){
cin>>n>>m;
init(n);//Although n and m are global variables, it is more understandable to write parameter transfer in this way.
read(m);
dijkstra(1);//Start at the first point (of course, here can also start at another point)
for(int i=2;i<=n;i++){//The shortest distance output to other points
cout<<"1 reach"<<i<<"The shortest distance is:"<<dis[i]<<"\n";
}
cout<<endl;
return 0;
}
As shown in the figure above, this is the case: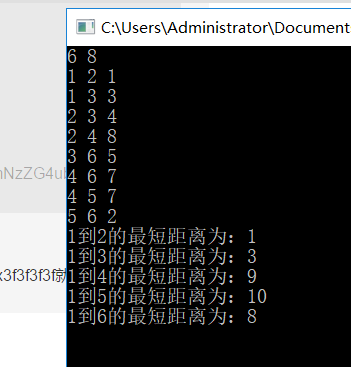
So the above is just the simplest Dijkstra algorithm. It is not enough for AC problem. So how to optimize it?
Here we will use priority queue + structure + adjacency table + Dijkstra; think about it is very complex, but really understand, it is still very useful; below is the AC code of this problem, but I believe that with Dijkstra + heap optimization, the algorithm efficiency will be greatly improved:
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
ll n,m;
struct End_Dis{
ll to,d,c;//To represents the point, d represents the soldier (also known as the distance problem), c is used to record whether the soldier is on the road.
End_Dis(ll a,ll b,ll cc=0):to(a),d(b),c(cc){}
bool operator < (const End_Dis tt) const{
return d>tt.d;//This is special, because the priority queue is from big to small, so I wrote one from big to small, and then this will make the priority queue from small to large (special place).
}
};
vector<End_Dis> a[100000*2];
ll book1[200010];//Has it been swept to mark this point?
ll Dijkstra(ll start){
ll dis[200010];
for(ll i=1;i<=n;i++) dis[i]=INF;//Initialize to INF first
book1[1]=0;//It means that this point has passed.
dis[1]=0;//The distance from oneself to oneself is 0.
priority_queue<End_Dis> q;//Establish a priority queue
q.push(End_Dis(1,0));//Put the first point in
while(!q.empty()) {//Cycle is non-empty
End_Dis t=q.top();
q.pop();
if(book1[t.to]) continue;//Indicates whether this point has been used or not.
for(ll i=0;i<a[t.to].size();i++){//With this point transfer station, enumerate other points to update 1 - the shortest distance of other points
End_Dis x=a[t.to][i];//Remove the object
if((t.c!=x.d)+t.d<dis[x.to]) {//Is the distance from 1 to h of the transfer station + whether the value before it is less than 1-x?
dis[x.to]=(t.c!=x.d)+t.d;
q.push(End_Dis(x.to,dis[x.to],x.d));//Find it and bring in the point behind the transfer station.
}
}
}
return dis[n];
}
void read(ll m){
ll aa,bb,cc;
for(ll i=1;i<=m;i++){
scanf("%lld %lld %lld",&aa,&bb,&cc);
a[aa].push_back(End_Dis(bb,cc));
a[bb].push_back(End_Dis(aa,cc));
}
}
void init(ll n){
for(ll i=1;i<=n;i++){
a[i].clear();
}
}
int main(){
while(~scanf("%lld %lld",&n,&m)){
init(n);
read(m);
int ans=Dijkstra(1);
if(ans==INF)puts("-1");
else printf("%lld\n",ans);
}
return 0;
}
Of course, this question gives me some inspiration. I used to understand the Dijkstra algorithm, but that is very shallow. I believe this heap optimization can be used to solve the graph problem I gave earlier:
Just change the code:
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
ll n,m;
struct End_Dis{
ll to,d;//To denotes a point, d denotes the distance from the previous point to that point.
End_Dis(ll a,ll b):to(a),d(b){}/// Here the constructor has a convenient addition point.
bool operator < (const End_Dis tt) const{//This is useful when using priority queues
return d>tt.d;//This is special, because the priority queue is from big to small, so I wrote one from big to small, and then this will make the priority queue from small to large (special place).
}
};
vector<End_Dis> a[100000*2];//Use adjacency tables to store other points that a point can reach, such as a[aa][i].to denote the point from AA to to
ll book1[200010];//Used to mark whether this point has been swept or not// Used to mark whether this point has been used as a transit station
ll Dijkstra(ll start){
ll dis[200010];//Represents distance
for(ll i=1;i<=n;i++) dis[i]=INF;//Initialize to INF first
book1[start]=0;//Indicates that this point has passed // Here's what you need to pay attention to because this is different from the simplest Dijkstra algorithm.
dis[start]=0;//The distance from oneself to oneself is 0.
priority_queue<End_Dis> q;//Establish a priority queue
q.push(End_Dis(start,0));//Put the first point in
while(!q.empty()) {//Cycle is non-empty
End_Dis t=q.top();
q.pop();
if(book1[t.to]) continue;//Indicates whether this point has been used or not.
for(ll i=0;i<a[t.to].size();i++){//With this point transfer station, enumerate other points to update 1 - the shortest distance of other points
End_Dis x=a[t.to][i];//Objects that take out the point to which t.to can reach
if(dis[x.to]>dis[t.to]+x.d){//Comparison of the distance from start to x.to point and from start to t.to with the sum of t.to to x.d
//Update the distance of this point
dis[x.to]=dis[t.to]+x.d;
q.push(End_Dis(x.to,dis[x.to]));//Add this point to the priority queue
}
}
}
return dis[n];
}
void read(ll m){//Because it's undirected graph
ll aa,bb,cc;
for(ll i=1;i<=m;i++){
scanf("%lld %lld %lld",&aa,&bb,&cc);
a[aa].push_back(End_Dis(bb,cc));
a[bb].push_back(End_Dis(aa,cc));
}
}
void init(ll n){//Every clearance
for(ll i=1;i<=n;i++){
a[i].clear();
}
}
int main(){
while(~scanf("%lld %lld",&n,&m)){
init(n);
read(m);
int ans=Dijkstra(1);
if(ans==INF)puts("-1");//If you can't reach n point that long, output -1
else printf("reach n The shortest path of the point is: %lld\n",ans);
}
return 0;
}
This is what I think is the best version of the Dijkstra algorithm.