Preface

Weekly Contest 122 Of Minimum string starting from leaf node:

Given a binary tree whose root node is root, each node in the book has a value from 0 to 25, respectively representing the letters' a 'to' z ': the value 0 represents' a', the value 1 represents' b ', and so on.

Find the smallest string in dictionary order, starting from a leaf node of the tree and ending at the root node.

(tip: any shorter prefix in a string is smaller in the dictionary order: for example, "ab" is smaller than "aba" in the dictionary order. Leaf node refers to a node without child nodes.)

Example 1: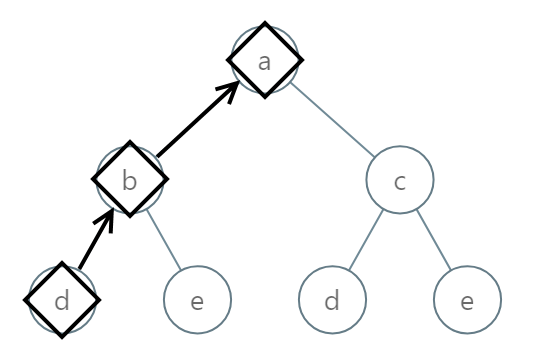

Input: [0,1,2,3,4,3,4]
Output: "dba"

Example 2: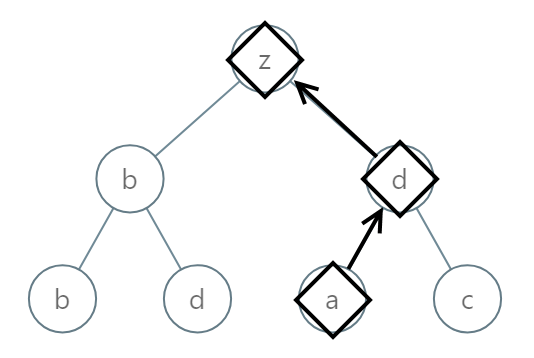

Input: [25,1,3,1,3,0,2]
Output: "adz"

Example 3: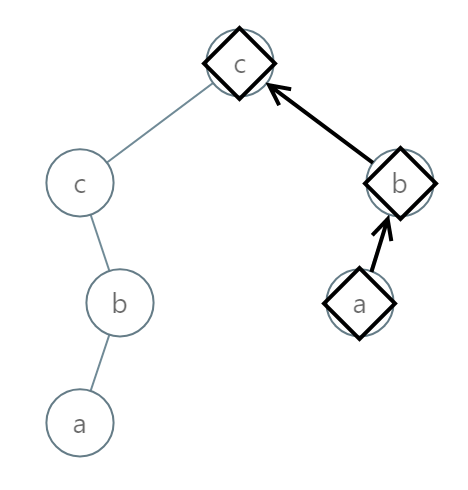

Input: [2,2,1,null,1,0,null,0]
Output: "abc"

Tips:

1. The number of nodes in a given tree is between 1 and 1000.
2. Each node in the tree has a value between 0 and 25.

Solving problems

This problem can be regarded as a special kind of middle order traversal, but the left and right subtree values need to be compared in the process of recursion.

Implementation code

   /**
     * 988. Minimum string starting from leaf node
     * On the basis of middle order traversal
     * Definition for a binary tree node.
     * public class TreeNode {
     *     int val;
     *     TreeNode left;
     *     TreeNode right;
     *     TreeNode(int x) { val = x; }
     * }
     * @param root
     * @return
     */
    public String smallestFromLeaf(TreeNode root) {
        // The node value is [0,25], so you need to add 'a' to get the corresponding char
        char c = (char)('a' + root.val);
        if (root.left == null && root.right == null) {//Left right subtree
            return "" + c;
        } else if (root.left == null) {//Left subtree is empty, traverse right subtree
            String str = smallestFromLeaf(root.right);
            return str + c;//
        } else if (root.right == null) {//Right subtree is empty, traverse left subtree
            return smallestFromLeaf(root.left) + c;
        } else {//Left and right subtrees are not empty
            String s1 = smallestFromLeaf(root.left);
            String s2 = smallestFromLeaf(root.right);
            if (s1.compareTo(s2) < 0) {//Compare the minimum strings of left and right subtrees
                return s1 + c;
            } else {
                return s2 + c;
            }
        }
    }