In the previous chapter, we introduced heap. In this chapter, we introduced a new tree structure, Segment Tree.

Why use segment trees?

For a class of problems, we are concerned with line segments (or intervals).

The most classic line segment tree problem, interval dyeing: there is a wall, the length is n, each time select a section of wall for dyeing.

After 4-9 is dyed orange, green is drawn for 7-15. Orange is covered with green.

1-5 is painted blue, 6-12 is painted red.

How many colors can we see after m operations? How many colors can we see in [i, j] interval after m operations?

The whole question: We focus on intervals. The dyeing operation (update interval) query operation (query interval) dyeing operation traverses the interval once, and the query traverses the interval once.

Another Classical Problem: Interval Query

Query the maximum, minimum, or interval number sum of an interval [i, j]. Essential: Statistical query based on intervals

For example: the most consumed registered users in 2017? The least consumed users? The users with the longest learning time? The total number of celestial bodies in a space zone?

A dynamic query is not limited to the historical data of 2017. It is possible that in 2018 he is still consuming and the data is still changing. A celestial body runs from one interval to another.

For this kind of interval class problem, using segment tree, its time complexity will change to O(logn) level. When you see logn, you should realize that segment tree is also a binary tree structure.

For a given interval, two operations are updated: updating the value of an element or an interval in the interval; querying: the maximum, minimum, or interval number and interval number of an interval [i, j].

Realization: (Section tree interval itself is fixed, 2017 registered users)

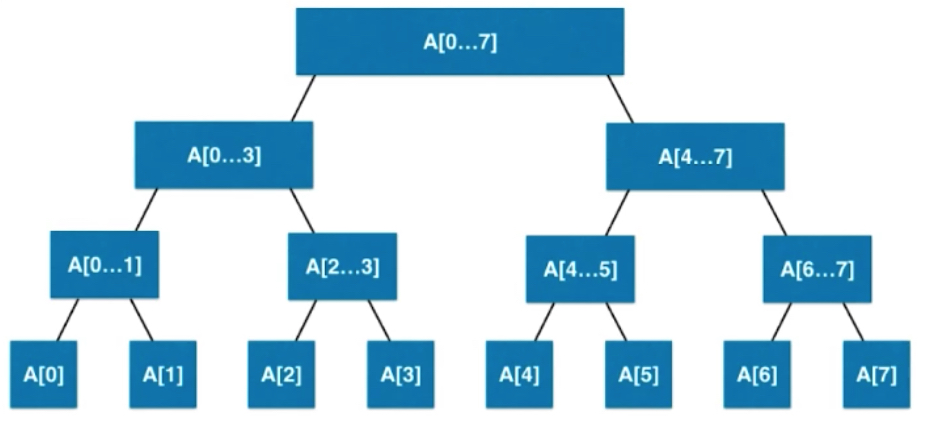
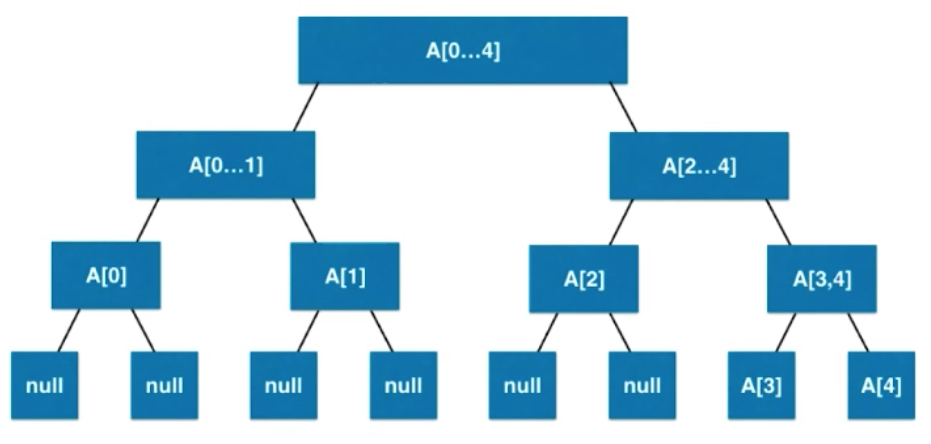
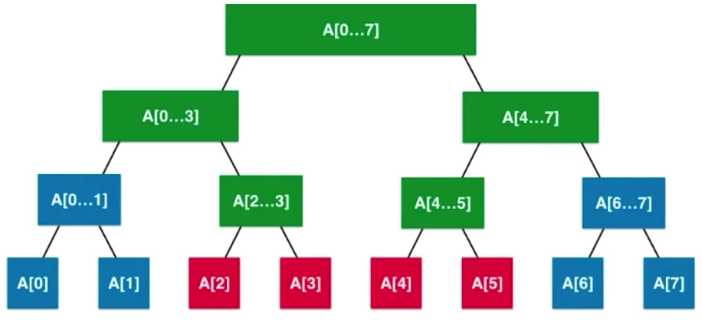
Like all binary trees, it has one node. Each node represents the corresponding information in an interval. Take peace as an example. The last layer is a single node with an interval length of 1.

Query intervals 2-5 for synthesis.

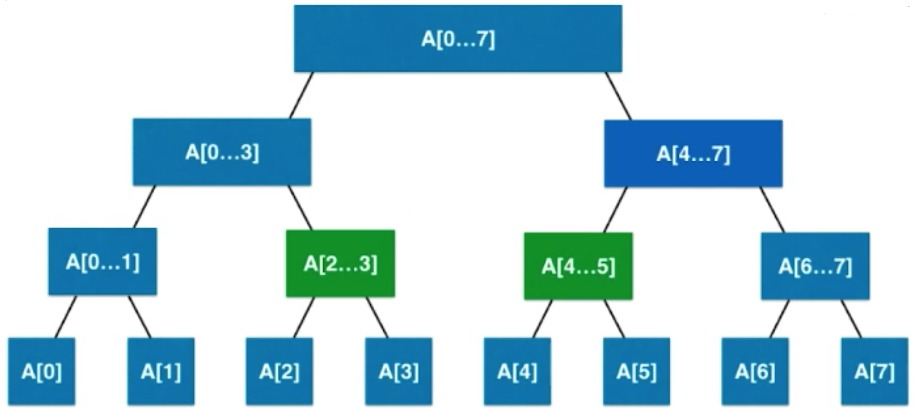
Basic Representation of Line Segment Tree

The nodes stored by each node correspond to the sum of numbers (sum, for example).

Eight elements, 2 ^ 3 power, full binary tree.

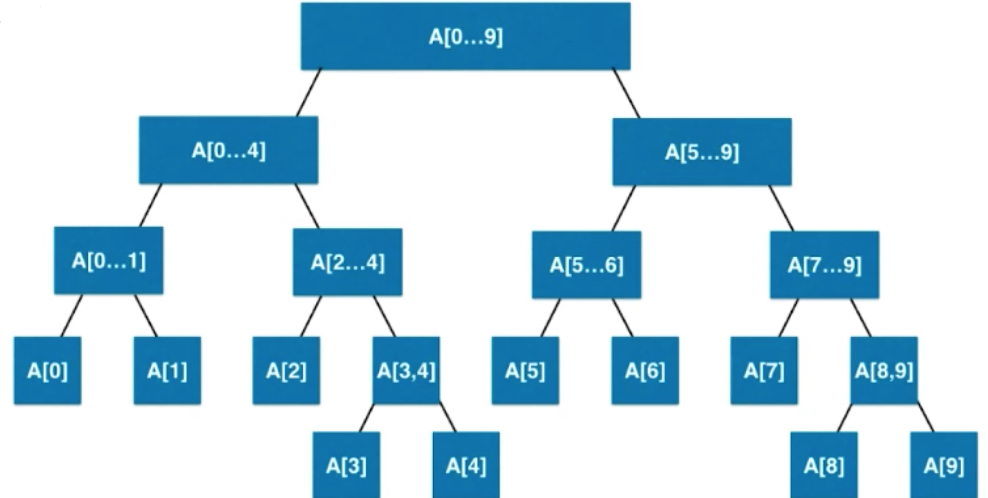
If you can't be divided equally, it's a little more on the right. Leaf nodes may be on the penultimate level.

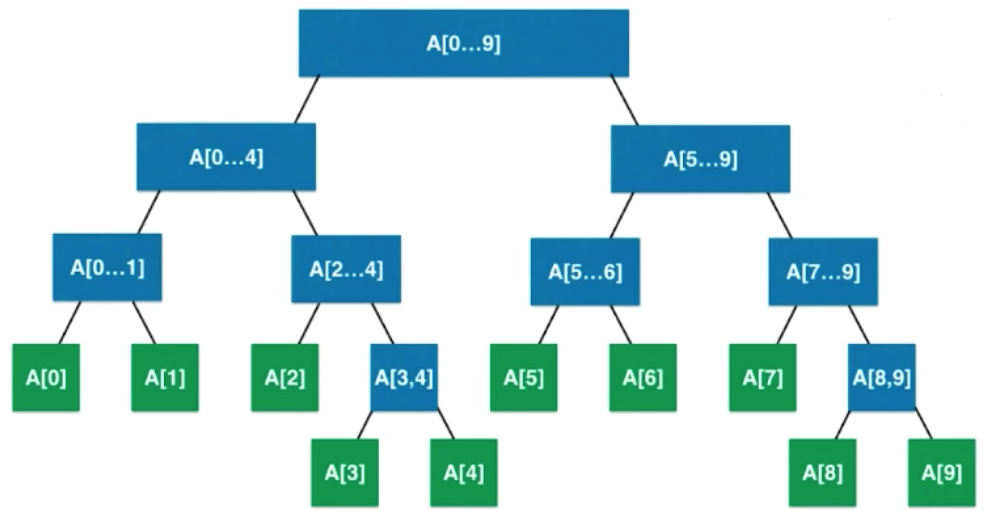
The segment tree is not a complete binary tree; the segment tree is a balanced binary tree. Definition of balanced binary tree: The difference between the maximum depth and the minimum depth is at most 1. For example, the leaf node in the figure above is located at either depth 4 or depth 5.

The heap is also a balanced binary tree, and the complete binary tree itself is a balanced binary tree. Although segment tree is not a complete binary tree, it satisfies the definition of segment tree.

Balanced binary trees do not degenerate into linked lists, but are still log-level.

The segment tree is a balanced binary tree and can still be represented by an array. As a full binary tree, if there are n elements in an interval, how many nodes does the array represent?

For full binary tree: h layer, there are 2 ^ h-1 nodes (about 2h), the last layer (h-1 layer), there are 2(h-1) nodes, the number of nodes in the last layer is roughly equal to the sum of all the nodes in the front layer.

If n=2^k requires only 2n space; in the worst case, if n=2^k+1 requires 4n space

If there are N element arrays in the interval, how many nodes are needed? 4 n space is needed.
Our segment tree does not consider adding elements, i.e. fixed intervals, but uses 4n static space (which is guaranteed to be absolutely complete).

It can be seen that a lot of space is wasted. Modern computer space changes time. This part of waste can not be wasted. The expansion part can be solved. Node storage can avoid waste.

package cn.mtianyan.segment;

public class SegmentTree<E> {

    private E[] tree;
    private E[] data; // Store copies of entire segment tree data

    public SegmentTree(E[] arr) {

        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++)
            data[i] = arr[i];

        tree = (E[]) new Object[4 * arr.length];
    }

    /**
     * Get the array size
     *
     * @return
     */
    public int getSize() {
        return data.length;
    }

    /**
     * Pass in index to get the location data
     *
     * @param index
     * @return
     */
    public E get(int index) {
        if (index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal.");
        return data[index];
    }

    /**
     * Returns the index of the left child node of the element represented by an index in the array representation of a complete binary tree
     *
     * @param index
     * @return
     */
    private int leftChild(int index) {
        return 2 * index + 1;
    }

    /**
     * Returns the index of the right child node of the element represented by an index in the array representation of a complete binary tree
     *
     * @param index
     * @return
     */
    private int rightChild(int index) {
        return 2 * index + 2;
    }
}

There is no need to find the father node of a node in the segment tree. Line segment tree space 4n.

Create a segment tree.

The information stored in the root node is the synthesis of the two children's information (recursive), and how to merge is determined by the business. Recursively, there is only one element per se.

package cn.mtianyan.segment;

public interface Merger<E> {
    E merge(E a, E b);
}

public class SegmentTree<E> {

    private E[] tree;
    private E[] data; // Store copies of entire segment tree data
    private Merger<E> merger; // Users can pass in merge rules

    public SegmentTree(E[] arr, Merger<E> merger) {
        this.merger = merger;
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++)
            data[i] = arr[i];

        tree = (E[]) new Object[4 * arr.length];
        buildSegmentTree(0, 0, arr.length - 1); // The root node index is 0, and the left and right endpoints of the interval.
    }

    /**
     * Create a line segment tree representing the interval [l...r] at the location of treeIndex
     *
     * @param treeIndex
     * @param l
     * @param r
     */
    private void buildSegmentTree(int treeIndex, int l, int r) {

        // Recursion to the end.
        if (l == r) {
            tree[treeIndex] = data[l];
            return;
        }

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);

        // We need to know the corresponding interval range of left and right subtrees.
        // int mid = (l + r) / 2; integer exception possible
        int mid = l + (r - l) / 2;
        buildSegmentTree(leftTreeIndex, l, mid);
        buildSegmentTree(rightTreeIndex, mid + 1, r);

        // Business-related value consolidation
        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    /**
     * Traverse the node median information in the print tree.
     * @return
     */
    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        res.append('[');
        for(int i = 0 ; i < tree.length ; i ++){
            if(tree[i] != null)
                res.append(tree[i]);
            else
                res.append("null");

            if(i != tree.length - 1)
                res.append(", ");
        }
        res.append(']');
        return res.toString();
    }

Here, parameters are added to the constructor so that users can pass in merger rules to change the merge rules within the class. Similar to the incoming element comparator in the precedence queue in the previous chapter.

package cn.mtianyan;

import cn.mtianyan.segment.SegmentTree;

public class Main {

    public static void main(String[] args) {

        Integer[] nums = {-2, 0, 3, -5, 2, -1};
//        SegmentTree<Integer> segTree = new SegmentTree<>(nums,
//                new Merger<Integer>() {
//                    @Override
//                    public Integer merge(Integer a, Integer b) {
//                        return a + b;
//                    }
//                });

        SegmentTree<Integer> segTree = new SegmentTree<>(nums,
                (a, b) -> a + b);
        System.out.println(segTree);
    }
}

The implementation of anonymous inner classes can be rewritten to Lambda expressions, and the input (a,b) returns a+b.

Query of Line Segment Tree

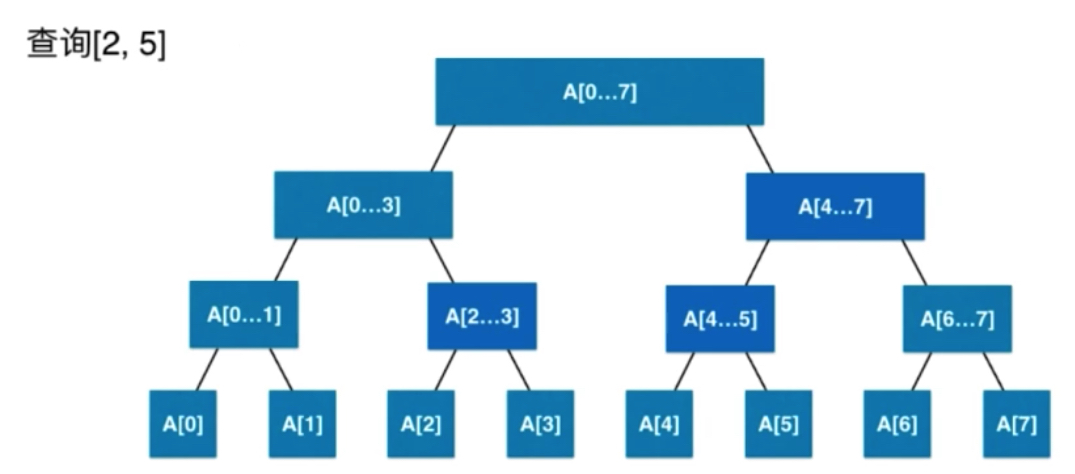
It is equivalent to querying the sum of all elements in the 2-5 interval. From the root node down, we know the partition location, the left node queries [2,3] the right node queries [4,5], after finding two nodes, we can merge.

Depending on the height of the tree, the height is at the logn level.

    /**
     * Returns the value of the interval [queryL, queryR]
     *
     * @param queryL
     * @param queryR
     * @return
     */
    public E query(int queryL, int queryR) {

        if (queryL < 0 || queryL >= data.length ||
                queryR < 0 || queryR >= data.length || queryL > queryR)
            throw new IllegalArgumentException("Index is illegal.");

        return query(0, 0, data.length - 1, queryL, queryR);
    }

    /**
     * In the range of [l...r] in the line segment tree rooted by treeIndex, the value of the search interval [queryL...queryR]
     *
     * @param treeIndex We all pass in the interval range l r of the tree index; it can be packaged into a node class in a segment tree, where each node stores its interval range.
     * @param l
     * @param r
     * @param queryL
     * @param queryR
     * @return
     */
    private E query(int treeIndex, int l, int r, int queryL, int queryR) {
        // The left and right boundaries of the nodes coincide with the desired ones.
        if (l == queryL && r == queryR)
            return tree[treeIndex];

        int mid = l + (r - l) / 2;
        // The nodes of treeIndex are divided into [l...mid] and [mid+1...r].

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);

        // There is no relationship between the user's focus area and the left child.
        if (queryL >= mid + 1)
            // Go to the right subtree
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
            // The user focus area has nothing to do with the right
        else if (queryR <= mid)
            return query(leftTreeIndex, l, mid, queryL, queryR);

        // Part left, part right queryL R is split in two
        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult, rightResult);
    }

        System.out.println(segTree.query(0, 2));
        System.out.println(segTree.query(2, 5));
        System.out.println(segTree.query(0, 5));

Operation results:

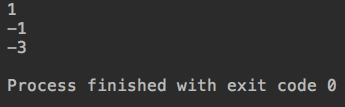
Running result 1 is -2+0+3; [0,5] all elements and

LeetCode Segment Tree Problem

https://leetcode-cn.com/problems/range-sum-query-immutable/description/

1. Region and Retrieval - Array immutable (not involving update operations of segment trees)

package cn.mtianyan.leetcode_303;

import cn.mtianyan.segment.SegmentTree;

class NumArray {

    private SegmentTree<Integer> segmentTree;
    public NumArray(int[] nums) {

        if(nums.length > 0){
            Integer[] data = new Integer[nums.length];
            for (int i = 0; i < nums.length; i++)
                data[i] = nums[i];
            segmentTree = new SegmentTree<>(data, (a, b) -> a + b);
        }

    }

    public int sumRange(int i, int j) {

        if(segmentTree == null)
            throw new IllegalArgumentException("Segment Tree is null");

        return segmentTree.query(i, j);
    }
}

When submitting our custom data structure, internal classes are changed to private, otherwise compilation errors will occur.

In the case of immutable arrays, sometimes better solutions can be obtained without using segment trees.

package cn.mtianyan.leetcode_303;

/**
 * Arrays are preprocessed.
 */
public class NumArray2 {

    private int[] sum; // sum[i] stores the sum of the first I elements, sum[0] = 0
    // That is sum[i] stores the sum of nums[0...i-1]
    // sum(i, j) = sum[j + 1] - sum[i]
    // There will be an offset here.
    public NumArray2(int[] nums) {

        sum = new int[nums.length + 1];
        sum[0] = 0;
        for(int i = 1 ; i < sum.length ; i ++)
            sum[i] = sum[i - 1] + nums[i - 1];
    }

    public int sumRange(int i, int j) {
        return sum[j + 1] - sum[i];
    }
}

The limitation of this problem is that the data is invariable, so other better schemes can be adopted. The better application scenario of segment tree is that the data will be updated and queried simultaneously.

Leetcode 307

Region and Retrieval - Array Modifiable

package cn.mtianyan.leetcode_307;

/**
 * Ideas for using sum arrays: TLE Time Limit Exceed timeout
 * update It's O(n) complexity, sumRange is still O(1)
 */
class NumArray {

    private int[] data; // Original array backup
    private int[] sum;

    public NumArray(int[] nums) {

        data = new int[nums.length];
        for (int i = 0; i < nums.length; i++)
            data[i] = nums[i];

        sum = new int[nums.length + 1];
        sum[0] = 0;
        for (int i = 1; i <= nums.length; i++)
            sum[i] = sum[i - 1] + nums[i - 1];
    }

    public int sumRange(int i, int j) {
        return sum[j + 1] - sum[i];
    }

    /**
     * update When an element is present, the whole array changes.
     *
     * @param index
     * @param val
     */
    public void update(int index, int val) {
        data[index] = val;
        // Reconstruct the sum array and update it from the index+1 position
        for (int i = index + 1; i < sum.length; i++)
            sum[i] = sum[i - 1] + data[i - 1];
    }
}

It was overtime when the teacher submitted it, but I submitted it both at LeetCode.com and LeetCode.cn, and there was no overtime.

Segment Tree Adds Update Operations.

    /**
     * Update the value of index location to e
     * @param index
     * @param e
     */
    public void set(int index, E e){

        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal");

        data[index] = e; // Replace the index position with a new value
        set(0, 0, data.length - 1, index, e);
    }

    /**
     * Update the value of index in the line segment tree rooted by treeIndex to e
     * @param treeIndex
     * @param l
     * @param r
     * @param index
     * @param e
     */
    private void set(int treeIndex, int l, int r, int index, E e){

        if(l == r){
            tree[treeIndex] = e;
            return;
        }
        // Find the leaf corresponding to index
        int mid = l + (r - l) / 2;
        // The nodes of treeIndex are divided into [l...mid] and [mid+1...r].

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if(index >= mid + 1)
            set(rightTreeIndex, mid + 1, r, index, e);
        else // index <= mid
            set(leftTreeIndex, l, mid, index, e);

        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

This process is very similar to the previous binary search tree updating. In fact, it is to find the location of index in the line segment tree, whether it is a left subtree or a right subtree. In the binary search tree, we compare the size relationship between the key and the current element. In the segment tree, you can see which half of index is after splitting it into two parts for the current interval.

The index position changes tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);

Question no. 307

package cn.mtianyan.leetcode_307;

import cn.mtianyan.segment.SegmentTree;

class NumArray2 {
    private SegmentTree<Integer> segTree;

    public NumArray2(int[] nums) {

        if(nums.length != 0){
            Integer[] data = new Integer[nums.length];
            for(int i = 0 ; i < nums.length ; i ++)
                data[i] = nums[i];
            segTree = new SegmentTree<>(data, (a, b) -> a + b);
        }
    }

    public void update(int i, int val) {
        if(segTree == null)
            throw new IllegalArgumentException("Error");
        segTree.set(i, val);
    }

    public int sumRange(int i, int j) {
        if(segTree == null)
            throw new IllegalArgumentException("Error");
        return segTree.query(i, j);
    }
}

You can see that using segment trees, the time is shorter. O(logn) was originally O(n)

For line segment trees, update and query operations can be completed within O(logn) time complexity. The process of creation is actually O(n) complexity, or O(4n) complexity, 4N space, each space assignment.

The data is updated dynamically and then queried for two operations. It is very suitable to use segment tree. This is a high-level data structure for competition.

More topics related to segment trees

Without participating in algorithm contest, segment tree is not a key point.

Line segment tree is not a complete binary tree, but it can be seen as a full binary tree, and then use arrays to store. This is consistent with the previous pile.

Understanding the structure of tree, the meaning of content stored by node is different, and the meaning of sub-tree is different. Give the structure a reasonable definition and deal with special problems efficiently.

Create line segment tree, query line segment tree, update line segment tree. After recursion, we should also integrate. In fact, it is a thought of post-order traversal.

Update an interval.

All elements in [2,5] interval + 3

logn finds the interval of interest, finds two nodes, and updates the nodes.

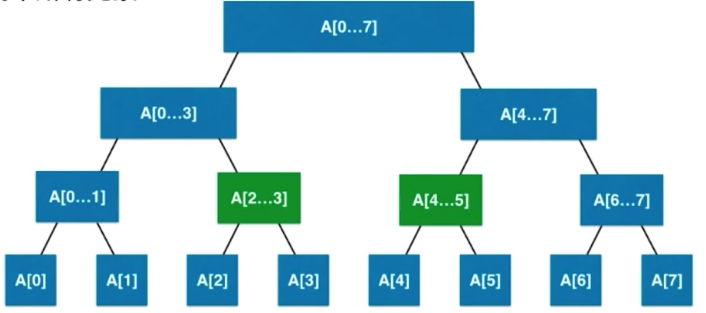
If it's a summation, add 6, because two elements in each node are added 3. The ancestor nodes are updated, and the leaf nodes are updated.

If the leaf node is also updated, it will be an O(n) complexity operation.

Laziness Updates, Laziness Spreads

Reducing the capacity of dynamic arrays has also been used. Use the lazy array to record the content of the last update. Next time you visit the node, if it is updated in the lazy array, do the operation again.

When the interval is updated, the logn is still used to query whether the node exists in the lazy array. Teachers will provide additional code.

Two-stack Line Segment Tree

We are currently a one-dimensional segment tree.

The matrix is divided into four blocks. Each node has four children, and each child is a smaller matrix.

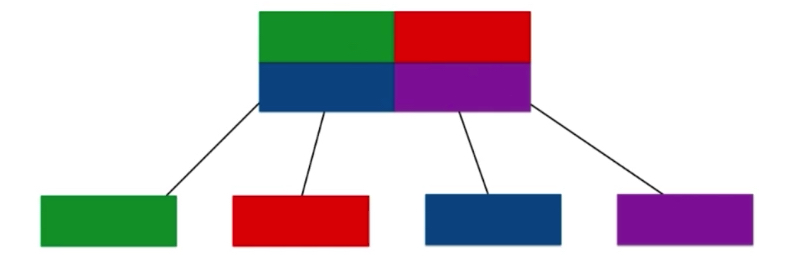
Higher dimensional data is still available, and large data units are broken down into smaller ones.

Dynamic Segment Tree

Storage space of array 4n, chain dynamic segment tree.

Node class: left boundary and right boundary of the interval, left and right children, their own values. To deal with many nodes, we can use the chain dynamic segment tree.

The amount of data is too large. We dynamically create dynamic segment trees according to our needs.

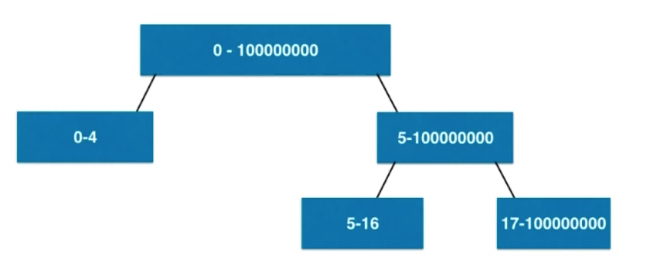
For example, when we only focus on 5-16, it can be implemented as shown above.

Another important data structure related to interval operations is the tree array Binary Index Tree.

Interval-related problems RMQ Range Minimum Query can also be solved by other good methods.

The next chapter goes on to look at a new tree structure, the unique n-fork tree, which can deal with string-related problems quickly, the dictionary tree.