catalogue
1, Longest common subsequence (discontinuous) -- dynamic programming
1.1 difference between longest common subsequence and longest common substring
1.2 the idea of finding the longest common subsequence (LCS): dynamic programming
II Longest common substring (continuous) -- sliding window
2.2 realization Method 1: sliding window
2.3 realization Method 2: dynamic programming (high complexity)
III Longest common prefix (continuous)
IV. longest increasing subsequence (discontinuous) -- greedy + dichotomy
5, Longest continuous increasing subsequence (continuous)
I Longest common subsequence (discontinuous) -- dynamic programming
Longest common subsequence-II_ Niuke Tiba_ Niuke network
Given two strings str1 and str2, the longest common subsequence of the two strings is output. "- 1" is returned if the longest common subsequence is empty. For the data given at present, there will only be one longest common subsequence

1.1 difference between longest common subsequence and longest common substring
- Subsequence: that is, the subsequence of a given sequence, which is the result of removing zero or more elements in a given sequence.
- Substring: a substring composed of any consecutive characters in a given string is called the substring of the string.
Explain again to a diagram:
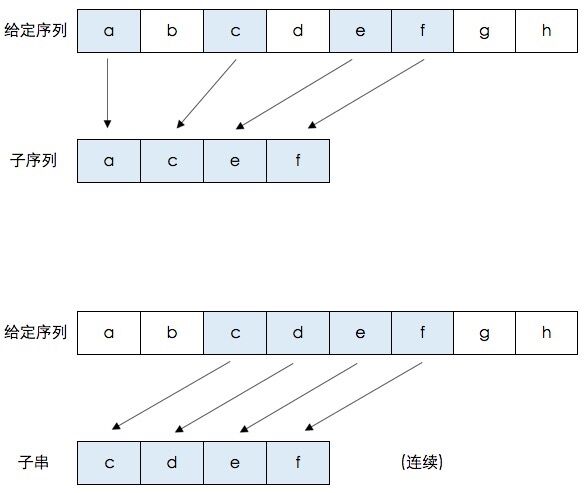
- Subsequence: {a,b,c,d,e,f,g,h}. Its subsequence example: {a,c,e,f} that is, after the elements B, D, G and H are removed, the result obtained by maintaining the original element sequence is the subsequence. Similarly, {a,h},{c,d,e} are its subsequences.
- Substring: {c,d,e,f} that is, the string composed of continuous elements c,d,e,f is the substring of a given sequence. Similarly, {a,b,c,d},{g,h} are all its substrings.
1.2 the idea of finding the longest common subsequence (LCS): dynamic programming
(1) Recursive formula: carry out dynamic programming and construct LCS array
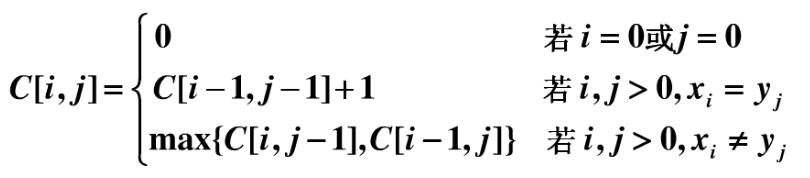
- c[i,j] represents the length of LCS of Xi and Yj;
- Where x = {X1... XM}, Y ={y1...yn}, xi = {X1... Xi}, Yj={y1... yj};
- If the last element of Xi and Yj is equal, the LCS of Xi and Yj is equal to the LCS of {Xi minus the last element} and {Yj minus the last element} Plus the last element where S1 and S2 are equal. C[i-1][j-1]+1;
- If the last element of Xi is not equal to the last element of Yj, the LCS of Xi and Yj is equal to: {Xi minus the LCS of the last element} and Yj, {Yj minus the largest sequence in the LCS of the last element} and Xi. max{C[i,j-1], C[i-1][j]}
(2) According to the LCS array, the longest common subsequence is constructed
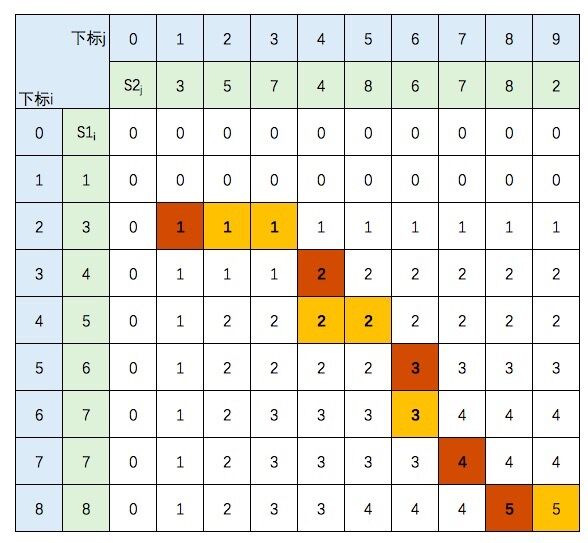
Take the LCS array of S1 = {1,3,4,5,6,7,7,8} and S2 = {3,5,7,4,8,6,7,8,2} as an example:
Note: there is not only one LCS for S1 and S2 in this paper. This paper does not focus on outputting all LCS of two sequences, but only introduces how to output one LCS through the above table.
2.1) the first result:
We will invert the LCS of S1 and S2 from the last element c[8][9]:
- c[8][9] = 5, and S1 [8]= S2 [9], so push back. The value of c[8][9] comes from the value of c[8][8] (because c[8][8] > C [7] [9]).
- c[8][8] = 5, And S1[8] = S2[8], so push back, and the value of C [8] [8] comes from c[7][7].
- And so on, if S1 [i] is encountered= S2 [J], and c[i-1][j] = c[i][j-1], please select one direction here (in case of such a situation later, the same direction is also selected).
The first result is:
This is the backward path. The brown square is the equal element, that is, LCS = {3,4,6,7,8}
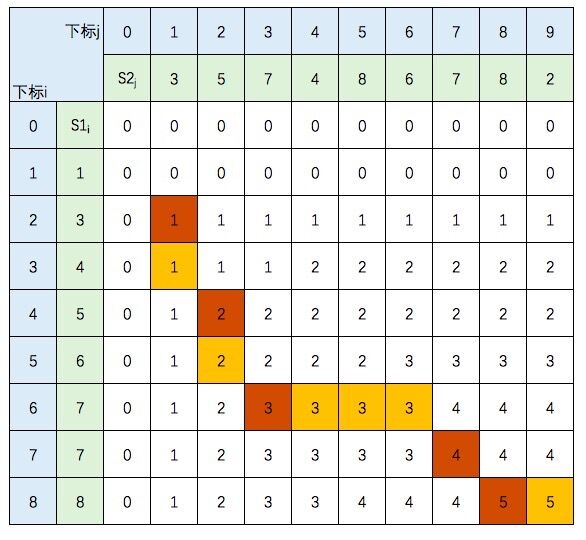
2.2) the second result:
If S1 [i] is encountered= S2 [J], and c[i-1][j] = c[i][j-1]. If you choose another direction, you will get another result, that is, LCS ={3,5,7,7,8}.
1.3 implementation
function LCS( s1 , s2 ) {
let l1 = s1.length;
let l2 = s2.length;
if(l1<=0 || l2<=0){
return -1;
}
let dp = [];
for(let i=0;i<=l1;i++){
dp[i] = []
for(let j=0;j<=l2;j++){
dp[i][j] = 0;
}
}
for(let i=1;i<=l1;i++){
for(let j=1;j<=l2;j++){
if(s1[i-1]===s2[j-1]){
dp[i][j] = dp[i-1][j-1]+1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])
}
}
}
//Push the LCS backward and forward according to dp
let res = [];
let m = l1,n = l2;
while(m>0 && n>0){
if(s1[m-1]===s2[n-1]){
res.unshift(s1[m-1]);
m--;
n--;
}else{
if(dp[m-1][n]>dp[m][n-1]){
m--;
}else{
n--;
}
}
}
if(res.length<=0){
return -1;
}else{
return res.join("");
}
}
module.exports = {
LCS : LCS
};II Longest common substring (continuous) -- sliding window
Longest common substring_ Niuke Tiba_ Niuke network

2.1 ideas
The idea of using sliding windows
2.2 realization Method 1: sliding window
/**
* longest common substring
* @param str1 string String the string
* @param str2 string String the string
* @return string character string
*/
function LCS( str1 , str2 ) {
//Look for a substring of a shorter string to see if it is a substring of a longer string
//1. Store a short string in STR1
if(str1.length > str2.length){
[str1, str2] = [str2, str1];
}
let len = str1.length;
let maxlen = 0; //Increase the maximum length in sequence. The maximum length is maxlen+1
let res = ''; //Longest common substring
//2. Look for substrings of shorter strings. Just look for a substring longer than the previous common substring
for(let i=0; i<len; i++){
// Current substring. Substring with length maxlen+1
let tempstr = str1.slice(i-maxlen, i+1);
if(str2.indexOf(tempstr) != -1){ //The substring exists in str2
res = tempstr;
maxlen++; //Continue to look for substrings with maximum length of maxlen+1
}
}
return res;
}
module.exports = {
LCS : LCS
};2.3 realization Method 2: dynamic programming (high complexity)
When you see the "maximum value" of two strings, you generally think of two-dimensional dp. It is natural to think of the length of the longest common substring of the first I characters of str1 and the first j characters of str2 as dp[i][j]. However, since the substring definition must be a continuous sequence of the original string, the definition cannot find a recursive relationship, so it needs to add a qualification - the length of the longest common substring ending with str1[i-1] and str2[j-1]. (the current longest common substring ends with str1[i-1] and str2[j-1]). maxlen is used to record the length of the current longest common substring.
/**
* longest common substring
* @param str1 string String the string
* @param str2 string String the string
* @return string character string
*/
function LCS( str1 , str2 ) {
//1. One of them is an empty string
if(str1 == null || str2 == null){
return "";
}
//2. Dynamic planning
let l1 = str1.length;
let l2 = str2.length;
let dp = new Array(l1);
let maxlen = 0;
let index = 0;
for(let i=0; i<l1; i++){
dp[i] = new Array(l2);
}
//initialization. If the initial value is not assigned to 0, it will directly become NaN when added
for(let i=0; i<l1; i++){
for(let j=0; j<l2; j++){
dp[i][j] = 0;
}
}
for(let i=0;i<l1;i++){
for(let j=0;j<l2;j++){
if(str1[i] == str2[j]){
if(i==0 || j==0){
dp[i][j] = 1;
}else{
dp[i][j] = dp[i-1][j-1]+1;
}
if(maxlen < dp[i][j]){
maxlen = dp[i][j];
index = i;
}
}//if
}//for
}//for
if(maxlen == 0) return "";
return str1.slice(index-maxlen+1, index+1);
}
module.exports = {
LCS : LCS
};III Longest common prefix (continuous)
Longest common prefix_ Niuke Tiba_ Niuke network
3.1 description
Give you a length of String array of n strs, write a function to find the longest public prefix in the string array and return this public prefix.
3.2 ideas:
- Sort the string array;
- Then just compare the first and last two strings;
- Find the longest common prefix of the first and last two characters;
3.3 realization:
/**
*
* @param strs string One dimensional array of strings
* @return string character string
*/
function longestCommonPrefix( strs ) {
if(!strs.length) return ""
if(strs.length === 1) return strs[0]
strs.sort();
let start = strs[0]; //Smallest string
let end = strs[strs.length-1]; //Maximum string
//Just look for the longest common prefix of start and end
let res = "";
for(let i=0; i<start.length;i++){
if(start[i]===end[i]){
res+=start[i];
}else{
break;
}
}
return res
}
module.exports = {
longestCommonPrefix : longestCommonPrefix
};
IV. longest increasing subsequence (discontinuous) -- greedy + dichotomy
Longest increasing subsequence_ Niuke Tiba_ Niuke network
4.1 description


4.2 ideas
1) Step 1: use greed + dichotomy to find the length of the longest increasing subsequence
Let's talk about the solution of greed + bisection, and illustrate the basic idea by giving an example. Assuming that the array arr is [2,3,1,2,3], the increasing subsequence is stored in the vec array, and the maximum increasing subsequence length ending with element i is stored in the maxLen array, then traverse the array arr and execute the following update rules:
- Initially, vec is [2], maxLen[1]
- Next, 3 is encountered. Since the last element of vec is less than 3, it is updated directly. vec is [2,3], maxLen[1,2]
- Next, we encounter 1. Since the last element of vec is greater than 1, we find the subscript of the first element greater than or equal to 1 in vec and replace it with 1. At this time, vec is [1,3], maxLen[1,2,1]
- Next, we encounter 2. Since the last element of vec is greater than 2, we find the subscript of the first element greater than or equal to 2 in vec and replace it with 2. At this time, vec is [1,2], maxLen[1,2,1,2]
- Next, 3 is encountered. Since the last element of vec is less than 3, it is updated directly. vec is [1,2,3] and maxLen is [1,2,1,2,3]
- At this time, the size of vec is the length of the longest increasing subsequence in the whole sequence (but vec is not necessarily the final solution of this problem)
2) Step 2: fill in the longest increasing subsequence
Assuming that our original array is arr1, the maxLen obtained is [1,2,3,1,3].
- Since the number of elements in the longest increasing subsequence from element arr[2] to arr[4] remains unchanged, it can be concluded that arr[2] > arr[4];
- Because we need to find the incremental subsequence with the smallest dictionary order, we choose the incremental subsequence ending in arr[4].
4.3 realization
- res array: used to store the current longest incremental subsequence
- maxLen array: stores the maximum increment subsequence length ending with element i
/**
* retrun the longest increasing subsequence
* @param arr int Integer one-dimensional array
* @return int Integer one-dimensional array
*/
function LIS( arr ) {
// 1. Array arr length is 0
if(arr.length<=0){
return [];
}
let res = [arr[0]]; //Current longest increment subsequence
let maxLen = new Array(arr.length).fill(1); //Maximum increment subsequence length ending with element i
// 2. Traverse the arr to find the longest increasing subsequence
for(let i=1;i<arr.length;i++){
//2.1 add res directly to the last element greater than the longest increasing subsequence res
if(arr[i]>res[res.length-1]){
res.push(arr[i]);
maxLen[i] = res.length;
}else{
//2.2 the last element less than res.
//Find the first element > = arr[i] in res by dichotomy and replace with arr[i]
let low = 0;
let high = res.length-1;
while(low<=high){
let mid = Math.floor((low+high)/2);
if(res[mid]<arr[i]){
low = mid+1;
}else if(res[mid]>arr[i]){
high = mid-1;
}else{
low = mid;
break;
}
}
res[low] = arr[i];
maxLen[i] = low+1;
}
}
//3. Fill in the longest increasing subsequence. Find from back to front
let result = [];
for(let i=arr.length-1,j=res.length;j>0;i--){
if(maxLen[i]==j){ //The increment subsequence ending with element i is the longest increment subsequence
result.unshift(arr[i]);
j--;
}
}
return result;
}
module.exports = {
LIS : LIS
};5, Longest continuous increasing subsequence (continuous)
5.1 problems


5.2 ideas
Traverse the array and record the current number of consecutive elements;
If it is discontinuous, set the count variable to 1;
5.3 realization
/**
* @param {number[]} nums
* @return {number}
*/
var findLengthOfLCIS = function(nums) {
//1. Array length < = 1
if(nums.length<=1){
return nums.length;
}
let res = 0;
let count = 1;
//2. Traverse the array. If the next element is incremented, count+1; Otherwise, count=1, count again
for(let i=0;i<nums.length-1;i++){
if(nums[i]<nums[i+1]){
count++;
}else{
count=1;
}
res = Math.max(count,res);
}
return res;
};