After reading this article, you can do the following two questions together:

• 104. Maximum depth of binary tree
• 559.n maximum depth of fork tree

Force button topic link (opens new window)

Given a binary tree, find its maximum depth. The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node.

Note: leaf nodes refer to nodes without child nodes.

Example: given binary tree [3,9,20,null,null,15,7],

  Returns its maximum depth 3.

1, Recursive method

You can use the pre order (left and right) or post order traversal (left, right and middle). The pre order is the depth, and the post order is the height. The height of the root node is the maximum depth of the binary tree, so in this problem, we calculate the maximum depth of the binary tree through the height of the root node in the later order.

In fact, many students did not think about this clearly, and many problem solutions did not explain it clearly. I first use postorder traversal (left, right, middle) to calculate the height of the tree.

• Determine the parameters and return value of the recursive function: the parameter is the root node of the incoming tree, and the return returns the depth of the tree, so the return value is of type int.

The code is as follows:

int getdepth(treenode* node)

• Determine the termination condition: if it is an empty node, it returns 0, indicating that the height is 0.

The code is as follows:

if (node == null) return 0;

• Determine the logic of single-layer recursion: first find the depth of its left subtree, then the depth of its right subtree, and finally take the value with the largest left and right depth, and then + 1 (plus 1 because the current intermediate node is included) is the depth of the tree with the current node as the root node.

The code is as follows:

int leftdepth = getdepth(node->left);       // Left
int rightdepth = getdepth(node->right);     // right
int depth = 1 + max(leftdepth, rightdepth); // in
return depth;

Therefore, the overall c + + code is as follows:

class solution {
public:
    int getdepth(treenode* node) {
        if (node == null) return 0;
        int leftdepth = getdepth(node->left);       // Left
        int rightdepth = getdepth(node->right);     // right
        int depth = 1 + max(leftdepth, rightdepth); // in
        return depth;
    }
    int maxdepth(treenode* root) {
        return getdepth(root);
    }
};

After code reduction, the c + + code is as follows:

class solution {
public:
    int maxdepth(treenode* root) {
        if (root == null) return 0;
        return 1 + max(maxdepth(root->left), maxdepth(root->right));
    }
};

The simplified code can't see what kind of traversal mode it is or the steps of the recursive trilogy. Therefore, if you are not proficient in the operation of binary tree, try not to learn directly from the simplified code.

Of course, the preamble can also be used for this problem. The code is as follows: (fully shows the process of seeking deep backtracking)

class solution {
public:
    int result;
    void getdepth(treenode* node, int depth) {
        result = depth > result ? depth : result; // in

        if (node->left == null && node->right == null) return ;

        if (node->left) { // Left
            depth++;    // Depth + 1
            getdepth(node->left, depth);
            depth--;    // Backtracking, depth-1
        }
        if (node->right) { // right
            depth++;    // Depth + 1
            getdepth(node->right, depth);
            depth--;    // Backtracking, depth-1
        }
        return ;
    }
    int maxdepth(treenode* root) {
        result = 0;
        if (root == 0) return result;
        getdepth(root, 1);
        return result;
    }
};

It can be seen that the traversal order of the previous order (middle left and right) is used, which is the real logic of seeking depth!

Note that the above code is to reflect the details. The code is simplified as follows:

class solution {
public:
    int result;
    void getdepth(treenode* node, int depth) {
        result = depth > result ? depth : result; // in
        if (node->left == null && node->right == null) return ;
        if (node->left) { // Left
            getdepth(node->left, depth + 1);
        }
        if (node->right) { // right
            getdepth(node->right, depth + 1);
        }
        return ;
    }
    int maxdepth(treenode* root) {
        result = 0;
        if (root == 0) return result;
        getdepth(root, 1);
        return result;
    }
};

2, Iterative method

Using iterative method, sequence traversal is the most appropriate, because the maximum depth is the number of layers of binary tree, which is very consistent with the way of sequence traversal. In the binary tree, the binary tree is traversed layer by layer. Record the number of traversed layers is the depth of the binary tree, as shown in the figure:

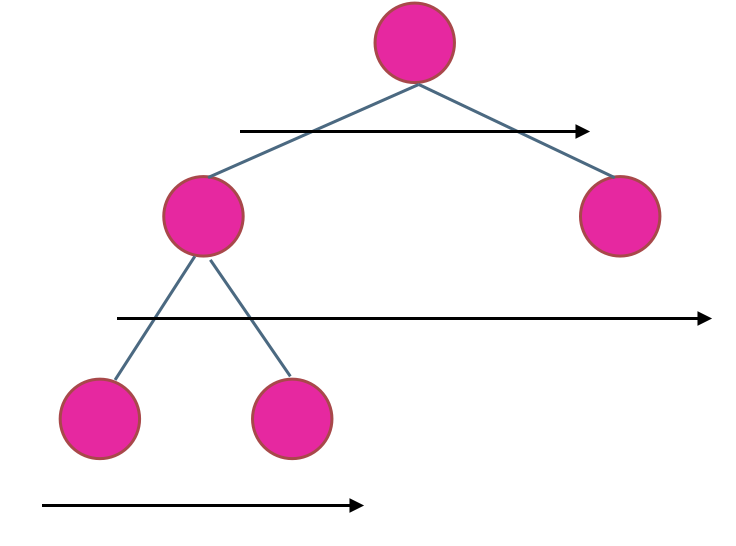
  Therefore, the iterative method of this problem is a template problem, which can be solved by using the template of binary tree sequence traversal.

If you are not clear about sequence traversal, you can read this article: Binary tree: sequence traversal! (opens new window)

The c + + code is as follows:

class solution {
public:
    int maxdepth(treenode* root) {
        if (root == null) return 0;
        int depth = 0;
        queue<treenode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // Recording depth
            for (int i = 0; i < size; i++) {
                treenode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return depth;
    }
};

By the way, we can solve the problem of the maximum depth of n-ary tree

3, 559.n maximum depth of fork tree

Force button topic link (opens new window)

Given an n-ary tree, find its maximum depth.

The maximum depth is the total number of nodes on the longest path from the root node to the farthest leaf node.

For example, given a 3-ary tree:

  We should return to its maximum depth, 3.

Idea:

Recursive method and iterative method can still be provided to solve this problem. The idea is the same as that of binary tree. The code is directly given as follows:

(1) Recursive method

c + + Code:

class solution {
public:
    int maxdepth(node* root) {
        if (root == 0) return 0;
        int depth = 0;
        for (int i = 0; i < root->children.size(); i++) {
            depth = max (depth, maxdepth(root->children[i]));
        }
        return depth + 1;
    }
};

(2) Iterative method

It is still sequence traversal, and the code is as follows:

class solution {
public:
    int maxdepth(node* root) {
        queue<node*> que;
        if (root != null) que.push(root);
        int depth = 0;
        while (!que.empty()) {
            int size = que.size();
            depth++; // Recording depth
            for (int i = 0; i < size; i++) {
                node* node = que.front();
                que.pop();
                for (int j = 0; j < node->children.size(); j++) {
                    if (node->children[j]) que.push(node->children[j]);
                }
            }
        }
        return depth;
    }
};