Given a binary tree and a target sum, judge whether there is a path from root node to leaf node in the tree. The sum of all node values on this path is equal to the target sum.
explain: A leaf node is a node that has no children.
Example: Given the following binary tree, and the target sum = 22
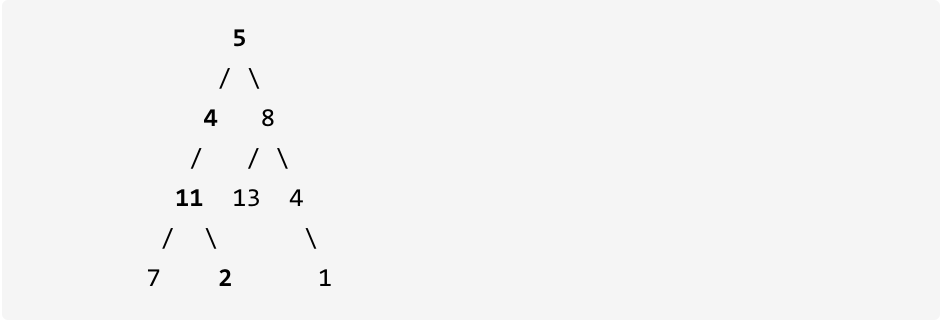
Returns true because there is a path 5 - > 4 - > 11 - > 2 from the root node to the leaf node with the target and 22.
1, Train of thought
In this problem, we need to traverse the path from the root node to the leaf node to see if the sum is the target sum.
1.1 recursion
You can use depth first traversal (the first, middle and last order of this problem is OK, it doesn't matter, because there is no processing logic in the node) to traverse the binary tree
- Determine the parameters and return types of recursive functions
Parameter: the root node of the binary tree and a counter are required. This counter is used to calculate whether the sum of one edge of the binary tree is exactly the target sum. The counter is of type int.
Let's look at the return value. When does a recursive function need a return value? When is the return value not required? Here are three points:
- If you need to search the whole binary tree and do not need to deal with the recursive return value, the recursive function does not return the value. (this situation is 113. Path summation ii introduced in the second half of this paper)
- If you need to search the whole binary tree and need to process the recursive return value, the recursive function needs to return the value. (in this case, we are 236. Nearest common ancestor of binary tree
- (opens new window) (introduced in)
- If you want to search for one of the qualified paths, recursion must return a value, because if you encounter a qualified path, you must return it in time. (situation of this topic)
In this problem, we need to find a path that meets the conditions, so the recursive function needs to return the value in time. What is the return type?
As shown in the figure:
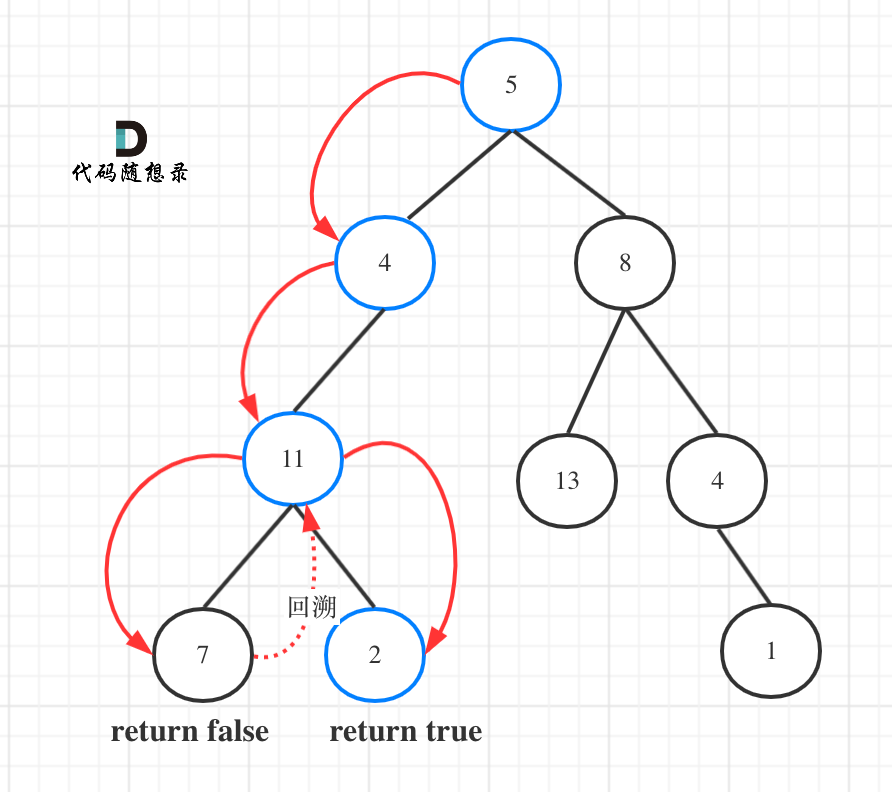
As can be seen from the figure, the traversal route does not traverse the whole tree, so the recursive function needs to return a value, which can be represented by bool type.
So the code is as follows:
bool traversal(treenode* cur, int count) // Note the return type of the function
- Determine termination conditions
First, how does the counter count the sum of this path?
Do not accumulate and judge whether it is equal to the target sum. The code is troublesome. You can use decrement to make the counter count initially the target sum, and then subtract the value on the traversal path node each time. If the last count == 0 and the leaf node is reached at the same time, it indicates that the target and node are found. If the leaf node is traversed and the count is not 0, it is not found.
The recursive termination condition code is as follows:
if (!cur->left && !cur->right && count == 0) return true; // Leaf node encountered and count is 0 if (!cur->left && !cur->right) return false; // If a leaf node is encountered and no suitable edge is found, return directly
- Determine the logic of single-layer recursion
Because the termination condition is to judge the leaf node, do not let the empty node enter the recursion in the process of recursion. The recursive function has a return value. If the recursive function returns true, it indicates that an appropriate path has been found and should be returned immediately.
The code is as follows:
if (cur->left) { // Left (empty nodes do not traverse)
// If the leaf node returns true, it returns true directly
if (traversal(cur->left, count - cur->left->val)) return true; // Notice the logic of backtracking
}
if (cur->right) { // Right (empty nodes do not traverse)
// If the leaf node returns true, it returns true directly
if (traversal(cur->right, count - cur->right->val)) return true; // Notice the logic of backtracking
}
return false;
The above code contains backtracking. Without backtracking, how to retreat and find another path.
Backtracking is hidden in traversal (cur - > left, count - cur - > left - > VAL), because count - cur - > left - > Val is directly passed in as a parameter. After the function ends, the value of count does not change.
In order to reflect the backtracking process, it can be changed to the following code:
if (cur->left) { // Left
count -= cur->left->val; // Recursion, processing nodes;
if (traversal(cur->left, count)) return true;
count += cur->left->val; // Backtracking, undo processing results
}
if (cur->right) { // right
count -= cur->right->val;
if (traversal(cur->right, count)) return true;
count += cur->right->val;
}
return false;
The overall code is as follows:
class solution {
private:
bool traversal(treenode* cur, int count) {
if (!cur->left && !cur->right && count == 0) return true; // Leaf node encountered and count is 0
if (!cur->left && !cur->right) return false; // Return directly when leaf node is encountered
if (cur->left) { // Left
count -= cur->left->val; // Recursion, processing nodes;
if (traversal(cur->left, count)) return true;
count += cur->left->val; // Backtracking, undo processing results
}
if (cur->right) { // right
count -= cur->right->val; // Recursion, processing nodes;
if (traversal(cur->right, count)) return true;
count += cur->right->val; // Backtracking, undo processing results
}
return false;
}
public:
bool haspathsum(treenode* root, int sum) {
if (root == null) return false;
return traversal(root, sum - root->val);
}
};
The code above is simplified as follows:
class solution {
public:
bool haspathsum(treenode* root, int sum) {
if (root == null) return false;
if (!root->left && !root->right && sum == root->val) {
return true;
}
return haspathsum(root->left, sum - root->val) || haspathsum(root->right, sum - root->val);
}
};
Is it found that the simplified code can not see the analysis process at all, so we should analyze the problem clearly and pursue code simplification. I have emphasized this many times!
1.2 iteration
If the stack is used to simulate recursion, what about backtracking? At this time, an element in the stack should record not only the node pointer, but also the sum of path values from the head node to the node. In c + +, we use the pair structure to store the elements in the stack.
Defined as: pair < tree node *, int > pair < node pointer, path value >
This is an element in the stack. The following code is the preamble traversal simulated by stack, as follows: (detailed comments)
class solution {
public:
bool haspathsum(treenode* root, int sum) {
if (root == null) return false;
// At this time, pair < node pointer, path value > should be placed in the stack
stack<pair<treenode*, int>> st;
st.push(pair<treenode*, int>(root, root->val));
while (!st.empty()) {
pair<treenode*, int> node = st.top();
st.pop();
// If the node is a leaf node and the path value of the node is equal to sum, then true is returned
if (!node.first->left && !node.first->right && sum == node.second) return true;
// Right node. When pressing in a node, record the path value of the node
if (node.first->right) {
st.push(pair<treenode*, int>(node.first->right, node.second + node.first->right->val));
}
// When pressing a node into the left node, the path value of the node is also recorded
if (node.first->left) {
st.push(pair<treenode*, int>(node.first->left, node.second + node.first->left->val));
}
}
return false;
}
};
2, 113. Path summation ii
Given a binary tree and a target sum, find all paths whose sum of paths from root node to leaf node is equal to the given target sum.
explain: A leaf node is a node that has no children.
Example: given the following binary tree, as well as the target and sum = 22,
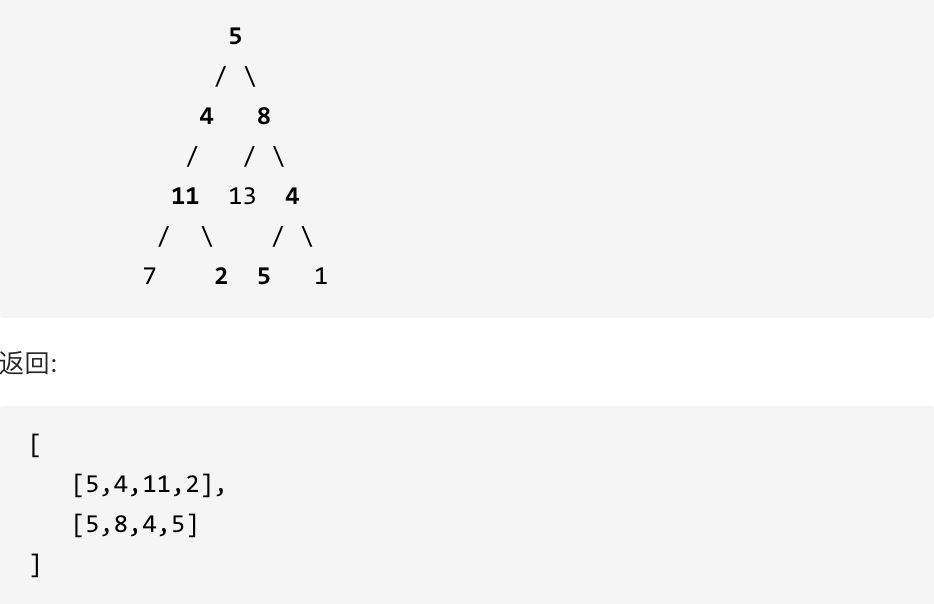
2.1 ideas
113. Path summation ii needs to traverse the whole tree and find all paths, so the recursive function does not return values!
As shown in the figure:
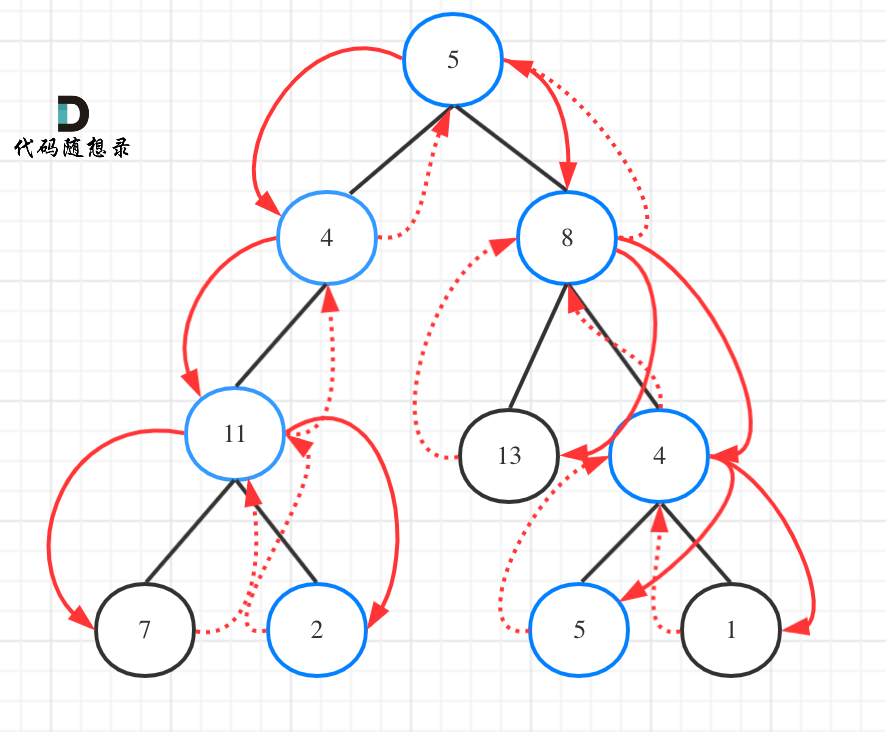
In order to reflect the details as much as possible, I write the following code (this code is not concise, but the logic is very clear)
class solution {
private:
vector<vector<int>> result;
vector<int> path;
// The recursive function does not need to return a value because we have to traverse the entire tree
void traversal(treenode* cur, int count) {
if (!cur->left && !cur->right && count == 0) { // A leaf node was encountered and a path with sum was found
result.push_back(path);
return;
}
if (!cur->left && !cur->right) return ; // If a leaf node is encountered and no suitable edge is found, return directly
if (cur->left) { // Left (empty nodes do not traverse)
path.push_back(cur->left->val);
count -= cur->left->val;
traversal(cur->left, count); // recursion
count += cur->left->val; // to flash back
path.pop_back(); // to flash back
}
if (cur->right) { // Right (empty nodes do not traverse)
path.push_back(cur->right->val);
count -= cur->right->val;
traversal(cur->right, count); // recursion
count += cur->right->val; // to flash back
path.pop_back(); // to flash back
}
return ;
}
public:
vector<vector<int>> pathsum(treenode* root, int sum) {
result.clear();
path.clear();
if (root == null) return result;
path.push_back(root->val); // Put the root node into the path
traversal(root, sum - root->val);
return result;
}
};
113. I didn't write the iterative method of path sum ii. It's troublesome and unnecessary to record all paths in an iterative way. If you are interested, you can study it further.
3, Summary
This article explains in detail when a recursive function needs a return value and what does not need a return value through 112. Path sum and 113. Path sum ii on leetcode.
These two questions are very good questions to master this knowledge. After reading this article, you will feel the difference between searching the whole tree and searching a certain path.
For 112. Path summation, I still give recursive method and iterative method. The practical iterative method of this problem will be more complex. It's enough to master the recursive method!