Complete leetcode intensive lecture of algorithm interview of large factory 23. And check the collection
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
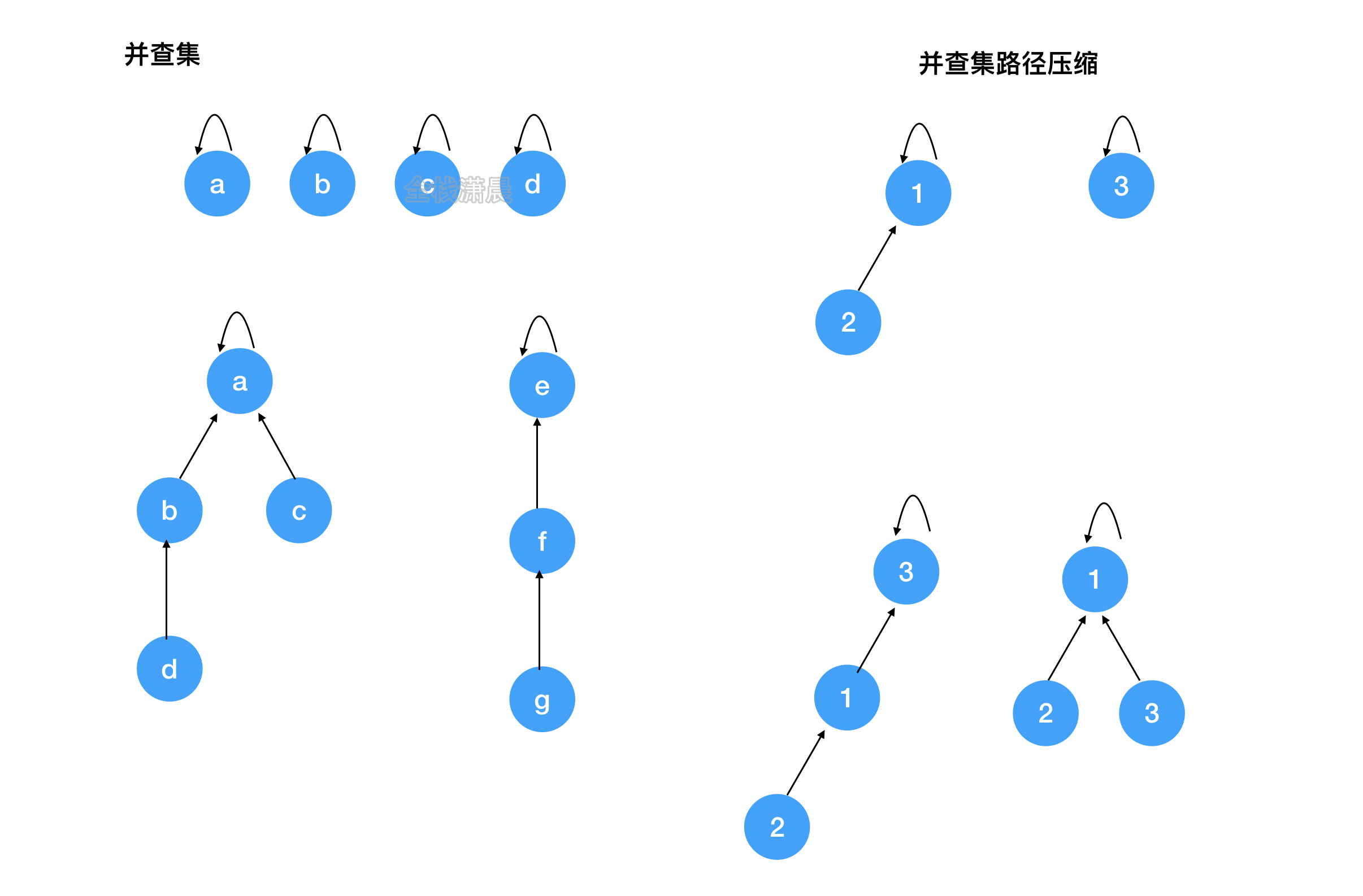
Union & find: used for merging and querying some elements
Find: determines which subset an element belongs to. It can be used to determine whether two elements belong to the same subset. Path compression is added, and the complexity is close to O(1)
Union: merge two subsets into the same set
// 0,1,2,3
//parent: 0,1,2,3
//size: 1,1,1,1
class UnionFind{
constructor(n){ //Construct a set of size n
this.count = n
this.parent = new Array(n)
this.size = new Array(n) // The size array records the size of each tree
for (let i = 0; i < n; i++) {
this.parent[i] = i; // You are your own parent
this.size[i] = 1;
}
}
union(p,q){ //Connected node p and node q, p and q are indexes
let rootP = this.find(p);
let rootQ = this.find(q);
if(rootP === rootQ) return
// A small number of elements are connected to a large number of elements, which is more balanced
if (this.size[rootP] > this.size[rootQ]) {
this.parent[rootQ] = rootP;
this.size[rootP] += this.size[rootQ];
} else {
this.parent[rootP] = rootQ;
this.size[rootQ] += this.size[rootP];
}
this.count--;
}
isConnected(p, q) { //Judge whether P and Q are connected
return this.find(p)=== this.find(q)
}
find(x) { //Find the root of node x
while (this.parent[x] != x) {
// Path compression
this.parent[x] = this.parent[this.parent[x]];
x = this.parent[x];
}
return x;
}
getCount() { //Returns the number of subsets
return this.count;
}
}
// 0,1,2,3
//parent: 0,1,2,3
//rank: 1,1,1,1
//Using rank optimization
class UnionFind {
constructor(n) { //Construct a set with n nodes
this.count = n //Total number of concurrent queries
this.parent = new Array(n)
this.rank = new Array(n) // The rank array records the weight of each tree
for (let i = 0; i < n; i++) {
this.parent[i] = i; // You are your own parent
this.rank[i] = 1; //Number of nodes on each collection
}
}
union(p, q) { //Connected node p and node q, p and q are indexes
let rootP = this.find(p);
let rootQ = this.find(q);
if (rootP === rootQ) return
// The elements with small depth are connected under the elements with large depth
if (this.rank[rootP] > this.rank[rootQ]) {
this.parent[rootQ] = rootP;
} else if (this.rank[rootP] < this.rank[rootQ]) {
this.parent[rootP] = rootQ;
} else {
this.parent[rootP] = rootQ;
this.rank[rootQ]++
}
this.count--;
}
isConnected(p, q) { //Judge whether P and Q are connected
return this.find(p) === this.find(q)
}
find(x) { //Find the root of node x
while (this.parent[x] != x) {
// Path compression
this.parent[x] = this.parent[this.parent[x]];
x = this.parent[x];
}
return x;
}
getCount() { //Returns the number of subsets
return this.count;
}
}200. Number of islands (medium)
The animation is too large. Click to view it
Method 1.dfs
- Idea: cycle the grid and traverse the four sides of each coordinate in depth first. Pay attention not to cross the boundary. When encountering land, add 1 and sink the surrounding land, so that the calculation will not be repeated
- Complexity: time complexity O(mn), m and N are the number of rows and columns. The space complexity is O(mn). In the worst case, all grids need recursion, and the recursion stack depth reaches m * n
js:
const numIslands = (grid) => {
let count = 0
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {//Cyclic grid
if (grid[i][j] === '1') {//If it is land, count + +,
count++
turnZero(i, j, grid)
}
}
}
return count
}
function turnZero(i, j, grid) {//Sinking the surrounding land
if (i < 0 || i >= grid.length || j < 0
|| j >= grid[0].length || grid[i][j] === '0') return //Check the validity of coordinates
grid[i][j] = '0'//Turn the land around into sea water
turnZero(i, j + 1, grid)
turnZero(i, j - 1, grid)
turnZero(i + 1, j, grid)
turnZero(i - 1, j, grid)
}java:
class Solution {
void dfs(char[][] grid, int r, int c) {
int nr = grid.length;
int nc = grid[0].length;
if (r < 0 || c < 0 || r >= nr || c >= nc || grid[r][c] == '0') {
return;
}
grid[r][c] = '0';
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int nr = grid.length;
int nc = grid[0].length;
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
dfs(grid, r, c);
}
}
}
return num_islands;
}
}Method 2.bfs
- Idea: cycle the grid, breadth first traverse the surrounding coordinates, add 1 when encountering land, sink the surrounding land, and do not repeat the calculation of the number of land
- Complexity: time complexity O(mn),m and N are the number of rows and columns. The spatial complexity is O(min(m, n)), and the queue length needs to be able to accommodate the smaller of M and N in the worst case
js:
const numIslands = (grid) => {
let count = 0
let queue = []
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j] === '1') {
count++
grid[i][j] = '0' // Mark to avoid repeated traversal
queue.push([i, j]) //Join queue
turnZero(queue, grid)
}
}
}
return count
}
function turnZero(queue, grid) {
const dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]]
while (queue.length) {//When there are elements in the queue
const cur = queue.shift() //Take out the team head element
for (const dir of dirs) {//Breadth first diffusion in four directions
const x = cur[0] + dir[0]
const y = cur[1] + dir[1]
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] !== '1') {
continue
}//Check coordinate validity
grid[x][y] = '0' //Sunken land
queue.push([x, y]) //Four nodes join the queue
}
}
}java:
class Solution {
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int nr = grid.length;
int nc = grid[0].length;
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
grid[r][c] = '0';
Queue<Integer> neighbors = new LinkedList<>();
neighbors.add(r * nc + c);
while (!neighbors.isEmpty()) {
int id = neighbors.remove();
int row = id / nc;
int col = id % nc;
if (row - 1 >= 0 && grid[row-1][col] == '1') {
neighbors.add((row-1) * nc + col);
grid[row-1][col] = '0';
}
if (row + 1 < nr && grid[row+1][col] == '1') {
neighbors.add((row+1) * nc + col);
grid[row+1][col] = '0';
}
if (col - 1 >= 0 && grid[row][col-1] == '1') {
neighbors.add(row * nc + col-1);
grid[row][col-1] = '0';
}
if (col + 1 < nc && grid[row][col+1] == '1') {
neighbors.add(row * nc + col+1);
grid[row][col+1] = '0';
}
}
}
}
}
return num_islands;
}
}Method 3. Joint search
- Idea:
- Complexity: the time complexity is O(mn). The time complexity is actually O(mn * f(mn)). F is the complexity when using parallel search path compression, which is a constant, so it can be ignored. m and n are the number of rows and columns. The space complexity is O(mn), and the space of the search set
js:
class UnionFind {
constructor(n) { //Construct a set with n nodes
this.count = n //Total number of concurrent queries
this.parent = new Array(n)
this.size = new Array(n) // The size array records the weight of each tree
for (let i = 0; i < n; i++) {
this.parent[i] = i; // You are your own parent
this.size[i] = 1; //Number of nodes on each collection
}
}
union(p, q) { //Connected node p and node q, p and q are indexes
let rootP = this.find(p);
let rootQ = this.find(q);
if (rootP === rootQ) return
// A small number of elements are connected to a large number of elements, which is more balanced
if (this.size[rootP] > this.size[rootQ]) {
this.parent[rootQ] = rootP;
this.size[rootP] += this.size[rootQ];
} else {
this.parent[rootP] = rootQ;
this.size[rootQ] += this.size[rootP];
}
this.count--;
}
isConnected(p, q) { //Judge whether P and Q are connected
return this.find(p) === this.find(q)
}
find(x) { //Find the root of node x
while (this.parent[x] != x) {
// Path compression
this.parent[x] = this.parent[this.parent[x]];
x = this.parent[x];
}
return x;
}
getCount() { //Returns the number of subsets
return this.count;
}
}
var numIslands = function (grid) {
let m = grid.length
if (m === 0) return 0
let n = grid[0].length
const dummy = -1
const dirs = [[1, 0], [0, 1]]//Direction array right down
const uf = new UnionFind(m * n)
for (let x = 0; x < m; x++) {
for (let y = 0; y < n; y++)
if (grid[x][y] === '0') {//If the mesh is 0, merge with dummy
uf.union(n * x + y, dummy)
}
else if (grid[x][y] === '1') {//If the grid is 1, try down to the right
for (let d of dirs) {
let r = x + d[0]
let c = y + d[1]
if (r >= m || c >= n) continue //Coordinate legitimacy
if (grid[r][c] === '1') { //If 1 is below the right side of the current grid, it will be merged with the current grid
uf.union(n * x + y, n * r + c)
}
}
}
}
return uf.getCount() //Return and query the number of sets minus one
};Java:
class Solution {
class UnionFind {
int count;
int[] parent;
int[] rank;
public UnionFind(char[][] grid) {
count = 0;
int m = grid.length;
int n = grid[0].length;
parent = new int[m * n];
rank = new int[m * n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
parent[i * n + j] = i * n + j;
++count;
}
rank[i * n + j] = 0;
}
}
}
public int find(int i) {
if (parent[i] != i) parent[i] = find(parent[i]);
return parent[i];
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {
parent[rooty] = rootx;
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
} else {
parent[rooty] = rootx;
rank[rootx] += 1;
}
--count;
}
}
public int getCount() {
return count;
}
}
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int nr = grid.length;
int nc = grid[0].length;
int num_islands = 0;
UnionFind uf = new UnionFind(grid);
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
grid[r][c] = '0';
if (r - 1 >= 0 && grid[r-1][c] == '1') {
uf.union(r * nc + c, (r-1) * nc + c);
}
if (r + 1 < nr && grid[r+1][c] == '1') {
uf.union(r * nc + c, (r+1) * nc + c);
}
if (c - 1 >= 0 && grid[r][c-1] == '1') {
uf.union(r * nc + c, r * nc + c - 1);
}
if (c + 1 < nc && grid[r][c+1] == '1') {
uf.union(r * nc + c, r * nc + c + 1);
}
}
}
}
return uf.getCount();
}
}547. Number of provinces(medium)
Method 1.dfs
- Idea: depth first traversal, whether visited records have been accessed, loop the province array, and recursively find the adjacent cities in the isConnected matrix.
- Complexity: time complexity O(n^2), n is the number of cities, traversing each element in the matrix. Space complexity O(n), recursion depth no more than n
js
var findCircleNum = function(isConnected) {
const rows = isConnected.length;
const visited = new Set();//Whether the record has been accessed
let count = 0;//Number of provinces
for (let i = 0; i < rows; i++) {
if (!visited.has(i)) {//If you haven't visited
dfs(isConnected, visited, rows, i);//Depth first traversal
count++;//Number of provinces + 1
}
}
return count;
};
const dfs = (isConnected, visited, rows, i) => {
for (let j = 0; j < rows; j++) {
if (isConnected[i][j] == 1 && !visited.has(j)) {//If i, j are connected
visited.add(j);
dfs(isConnected, visited, rows, j);//Recursive traversal
}
}
};java:
class Solution {
public int findCircleNum(int[][] isConnected) {
int rows = isConnected.length;
boolean[] visited = new boolean[rows];
int count = 0;
for (int i = 0; i < rows; i++) {
if (!visited[i]) {
dfs(isConnected, visited, rows, i);
count++;
}
}
return count;
}
public void dfs(int[][] isConnected, boolean[] visited, int rows, int i) {
for (int j = 0; j < rows; j++) {
if (isConnected[i][j] == 1 && !visited[j]) {
visited[j] = true;
dfs(isConnected, visited, rows, j);
}
}
}
}Method 2.bfs
- Idea: breadth first traversal, follow the matrix, and then find adjacent cities to join the queue. If the queue is not empty, keep out of the queue and continue traversal
- Complexity: time complexity O(n^2), n is the number of cities, traversing each element in the matrix. The space complexity is O(n), and the longest queue and visited array is n
js:
var findCircleNum = function(isConnected) {
const rows = isConnected.length;
const visited = new Set();//Whether the record has been accessed
let count = 0;
const queue = new Array();
for (let i = 0; i < rows; i++) {
if (!visited.has(i)) {//Not visited
queue.push(i); //Join queue
while (queue.length) {//The queue is not empty to continue the cycle
const j = queue.shift();//Out of the team
visited.add(j);
for (let k = 0; k < rows; k++) {//Loop neighboring cities to join the queue
if (isConnected[j][k] === 1 && !visited.has(k)) {
queue.push(k);
}
}
}
count++;
}
}
return count;
};Java:
class Solution {
public int findCircleNum(int[][] isConnected) {
int rows = isConnected.length;
boolean[] visited = new boolean[rows];
int count = 0;
Queue<Integer> queue = new LinkedList<Integer>();
for (int i = 0; i < rows; i++) {
if (!visited[i]) {
queue.offer(i);
while (!queue.isEmpty()) {
int j = queue.poll();
visited[j] = true;
for (int k = 0; k < rows; k++) {
if (isConnected[j][k] == 1 && !visited[k]) {
queue.offer(k);
}
}
}
count++;
}
}
return count;
}
}Method 3. Joint search
- Idea: circular matrix, merge when encountering adjacent cities, and finally return and check the number of sets in the set
- Complexity: time complexity O(n^2). N is the number of cities. It needs to traverse the matrix. After path compression, it needs to find the parent node in the joint query set. The complexity is constant. The space complexity is O(n), that is, the space of the parent
js:
class UnionFind{
constructor(n){ //Construct a set of size n
this.count = n
this.parent = new Array(n)
this.size = new Array(n) // The size array records the size of each tree
for (let i = 0; i < n; i++) {
this.parent[i] = i; // You are your own parent
this.size[i] = 1;
}
}
union(p,q){ //Connected node p and node q, p and q are indexes
let rootP = this.find(p);
let rootQ = this.find(q);
if(rootP === rootQ) return
// A small number of elements are connected to a large number of elements, which is more balanced
if (this.size[rootP] > this.size[rootQ]) {
this.parent[rootQ] = rootP;
this.size[rootP] += this.size[rootQ];
} else {
this.parent[rootP] = rootQ;
this.size[rootQ] += this.size[rootP];
}
this.count--;
}
isConnected(p, q) { //Judge whether P and Q are connected
return this.find(p)=== this.find(q)
}
find(x) { //Find the root of node x
while (this.parent[x] != x) {
// Path compression
this.parent[x] = this.parent[this.parent[x]];
x = this.parent[x];
}
return x;
}
getCount() { //Returns the number of subsets
return this.count;
}
}
var findCircleNum = function(isConnected) {
const rows = isConnected.length;
const uf = new UnionFind(rows)
for (let i = 0; i < rows; i++) {
for (let j = i + 1; j < rows; j++) {
if (isConnected[i][j] == 1) {//Merger of adjacent cities
uf.union(i, j);
}
}
}
return uf.getCount();
};Java:
class Solution {
public int findCircleNum(int[][] isConnected) {
int rows = isConnected.length;
int[] parent = new int[rows];
for (int i = 0; i < rows; i++) {
parent[i] = i;
}
for (int i = 0; i < rows; i++) {
for (int j = i + 1; j < rows; j++) {
if (isConnected[i][j] == 1) {
union(parent, i, j);
}
}
}
int count = 0;
for (int i = 0; i < rows; i++) {
if (parent[i] == i) {
count++;
}
}
return count;
}
public void union(int[] parent, int index1, int index2) {
parent[find(parent, index1)] = find(parent, index2);
}
public int find(int[] parent, int index) {
if (parent[index] != index) {
parent[index] = find(parent, parent[index]);
}
return parent[index];
}
}