1, Bracket matching problem

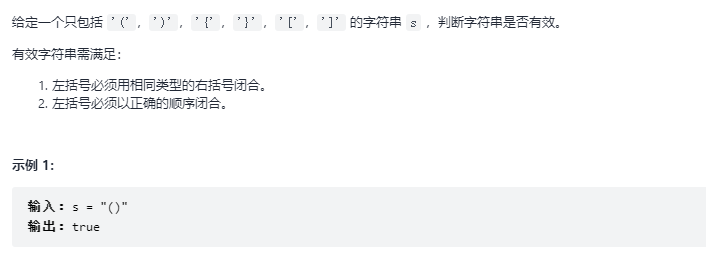
1. Title Requirements:  

 

2. General idea

After traversing the string, if it is an open parenthesis, let it enter the stack. If it is a right parenthesis, let it match the top element of the stack (provided that there are elements in the stack). If the matching is successful, let the top element out of the stack. If the matching fails, return false until traversing the string. If there are no elements in the stack, return true.

3. Code implementation

bool isValid(char * s){
    Stack stack;
    StackInit(&stack);//initialization
    int i = 0;
    while(s[i] != '\0'){
        //Push 
        if(s[i] == '{' || s[i] == '[' || s[i] == '('){
            StackPush(&stack,s[i]);
        }else{
            //When stack is empty
            if(StackEmpty(&stack)){
                StackDestroy(&stack);  //Destroy stack
                return false;
            }
            if((StackTop(&stack) == '(' && s[i] == ')') ||
               (StackTop(&stack) == '{' && s[i] == '}') ||
               (StackTop(&stack) == '[' && s[i] == ']')){  
                   StackPop(&stack);   //If it matches, it will be out of the stack
               }else{
                   //Mismatch
                   StackDestroy(&stack);
                   return false;
               }
        }
        i++;
    }
    //After traversal, the stack is empty
    if(StackEmpty(&stack)){
         StackDestroy(&stack);
        return true;
    }
    StackDestroy(&stack);
    return false;
}

2, Implement stack with queue

1. Title Requirements:  

2. General idea

It is implemented with two queues q1 and q2. To realize stack entry, you can select a queue that is not empty for queue entry operation (both queues can be started). Assuming that the elements are now in q1, to realize stack exit, put the elements in q1 into q2 until there is one element left in q1 and let it out of the queue.

3. Code implementation

//Stack with two queues
typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() {
    MyStack* ms = (MyStack*)malloc(sizeof(MyStack));
    if(ms == NULL){
        return NULL;
    }
    QueueInit(&ms->q1);
    QueueInit(&ms->q2);
    return ms;
}

void myStackPush(MyStack* obj, int x) {
    //Add elements to the queue that is not empty and simulate stacking
    if(QueueEmpty(&obj->q1) ){
        QueuePush(&obj->q2,x);
    }else{
        QueuePush(&obj->q1,x);
    }
}

int myStackPop(MyStack* obj) {
    //When q1 is empty, put the elements in q2 into q1 until there is only one element left in q2, and then q2 goes out of the queue to simulate the stack
    int ret = 0;
    if(QueueEmpty(&obj->q1)){
        while(QueueSize(&obj->q2) != 1){
            QueuePush(&obj->q1,QueueFront(&obj->q2));
            QueuePop(&obj->q2);
        }
        ret = QueueFront(&obj->q2);
        QueuePop(&obj->q2);
    }else{
         while(QueueSize(&obj->q1) != 1){
            QueuePush(&obj->q2,QueueFront(&obj->q1));
            QueuePop(&obj->q1);
        }
        ret = QueueFront(&obj->q1);
        QueuePop(&obj->q1);
    }
    return ret;
}
//The stack top element is equivalent to the queue tail element
int myStackTop(MyStack* obj) {
    if(QueueEmpty(&obj->q1)){
        return QueueBack(&obj->q2);
    }else{
        return QueueBack(&obj->q1);
    }
}

bool myStackEmpty(MyStack* obj) {
    if(QueueSize(&obj->q1) == 0 && QueueSize(&obj->q2) == 0){
        return true;
    }
    return false;
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

3, Implement queue with stack

1. Title Requirements

2. General idea

It is implemented with two stacks s1 and s2. s1 is used to simulate the queue and s2 is used to simulate the queue. Directly stack s1 when entering the queue; When leaving the queue, first judge whether there are elements in s2. If not, put the elements in s1 into s2, and then stack s2.

3. Code implementation

typedef struct {
    //s1 is used to enter the queue and s2 is used to exit the queue
    Stack s1;  
    Stack s2;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));
    if(q == NULL){
        return NULL;
    }
    StackInit(&q->s1);
    StackInit(&q->s2);
    return q;
}
//Queue
void myQueuePush(MyQueue* obj, int x) {
    StackPush(&obj->s1,x);
}
//Out of queue
int myQueuePop(MyQueue* obj) {
    //If s2 is not empty, move the elements in s1 to s2 first
    if(StackEmpty(&obj->s2)){
        while(!StackEmpty(&obj->s1)){
            StackPush(&obj->s2,StackTop(&obj->s1));
            StackPop(&obj->s1);
        }
    }
    int ret =  StackTop(&obj->s2);
    StackPop(&obj->s2);
    return ret;
    
}
//Return the header element, which is similar to that out of the queue
int myQueuePeek(MyQueue* obj) {
    if(StackEmpty(&obj->s2)){
        while(!StackEmpty(&obj->s1)){
            StackPush(&obj->s2,StackTop(&obj->s1));
            StackPop(&obj->s1);
        }
    }
   return StackTop(&obj->s2);
}

bool myQueueEmpty(MyQueue* obj) {
    if(StackEmpty(&obj->s1) && StackEmpty(&obj->s2)){
        return true;
    }
    return false;
}

void myQueueFree(MyQueue* obj) {
    if(obj != NULL){
        StackDestroy(&obj->s1);
        StackDestroy(&obj->s2);
        free(obj);
    }
}

4, Design a circular queue

1. Title Requirements

2. General idea

  Circular queues are stored in a sequential structure. Use two pointers to mark the head and tail of the team, as shown in the figure:

 

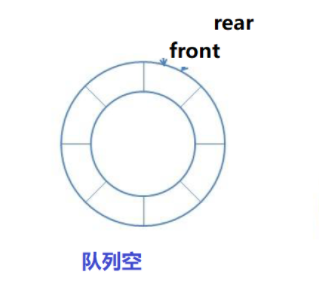
  However, there will be a problem, that is, when the queue is empty and the queue is full, the rear and front coincide, so it is impossible to judge whether the queue is full or empty. There are three ways to solve this problem:

Method 1:   We can use less storage space, as shown in the figure, which means that the queue is full.

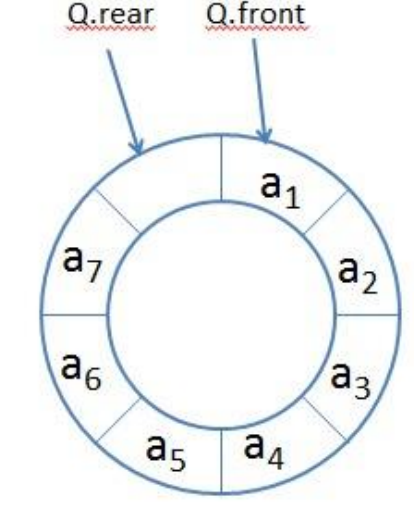
  Method 2: mark with a flag, set it to 0 at the beginning, set the flag to 1 when inserting elements, and set it to 0 when deleting elements; In this way, when front equals rear, judge the flag.

Method 3: use a count to count. Only when the count is zero, the queue is empty.

3. Code implementation

Method 3 is used here

typedef struct {
    int* array;//Store data
    int front; //Right
    int rear;  //Team tail
    int count; //count
    int N; //Queue capacity
} MyCircularQueue;

//initialization
MyCircularQueue* myCircularQueueCreate(int k) {
    //Apply for space for the queue first
    MyCircularQueue* q = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    if(q == NULL ){
        return NULL;
    }
    //Then apply for space for the array in the queue
    q->array = (int*)malloc(sizeof(int) * k);
    if(q->array == NULL){
        //If it fails, first release the space of the queue and pay attention to the rigor of the code
        free(q);
        return NULL;
    }
    q->front = q->rear = q->count = 0;
    q->N = k;
    return q;
}

//Determine whether the queue is empty
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return 0 == obj->count;
}

//Determine whether the queue is full
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return obj->count == obj->N;
}

//Queue
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj)){
        return false;
    }
    obj->array[obj->rear] = value;
    if(obj->rear == obj->N - 1){
        obj->rear = 0;
    }else{
        obj->rear++;
    }
    obj->count++;
    return true;
}
//Out of queue
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj)){
        return false;
    }
    if(obj->front == obj->N - 1){
        obj->front = 0;
    }else{
        obj->front++;
    }
    obj->count--;
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj)){
        return -1;
    }
    return obj->array[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj)){
        return -1;
    }
    //Pay attention to the calculation method of getting the tail element
    return obj->array[(obj->rear - 1 + obj->N) % obj->N];
}

//Free up space
void myCircularQueueFree(MyCircularQueue* obj) {
    if(obj){
        if(obj->array){
            free(obj->array);
        }
        free(obj);nhj 
    }
}