1. Stack
1.1 concept
Stack: a special linear table that allows insertion and deletion of elements only at a fixed end. One end for data insertion and deletion is called the top of the stack, and the other end is called the bottom of the stack. The data elements in the stack follow the principle of Last In First Out LIFO (Last In First Out).
Stack pressing: the stack insertion operation is called stack entering / stack pressing / stack entering, and the input data is at the top of the stack.
Stack out: stack deletion is called stack out. The output data is at the top of the stack.
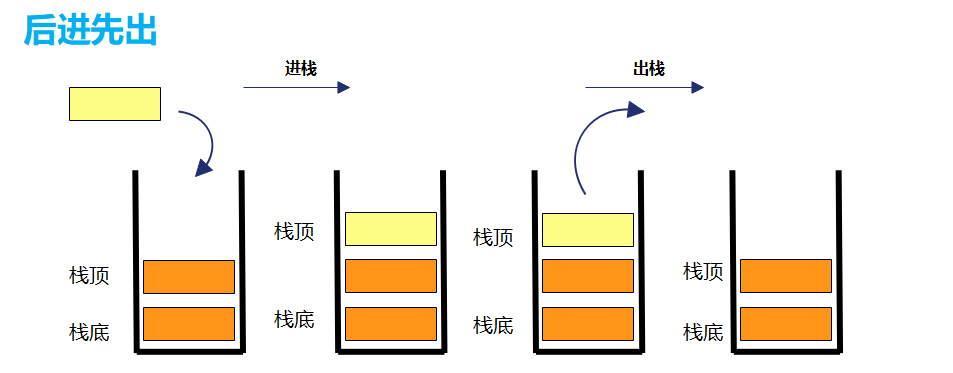
Push and Pop of Stack follow the principle of first in and last out, as shown in the figure:
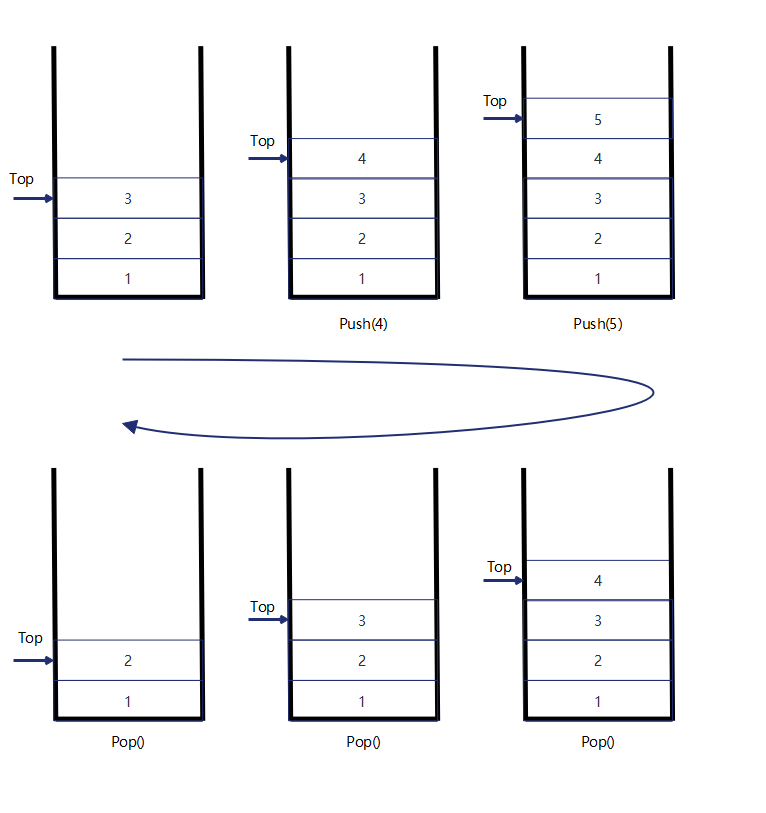
1.2 realization
- It is realized by using the sequence table, that is, it is realized by tail insertion + tail deletion
- Using a linked list, you can start and end
Header insertion: stack in O(1) stack out O(1)
Tail interpolation: stack in O(N) stack out O(N)
Relatively speaking, the implementation of sequence table is simpler, so we give priority to using sequence table to implement stack.
public class MyStack {
//Simple implementation, using the int element is enough, and the expansion problem is not considered
private int[] elem = new int[100];
private int usedSize = 0;// How many valid elements exist in the stack
//Push
public void push(int val){
elem[usedSize] = val;
usedSize++;
}
//Take the top element of the stack (the last element that comes in)
public int peek(){
return elem[usedSize - 1];
}
//Out of stack
public int pop(){
int ret = elem[usedSize - 1];
usedSize--;
return ret;
}
}
2. Queue
2.1 concept
Queue: a special linear table that only allows data insertion at one end and data deletion at the other end. The queue has a first in first out FIFO (first in first out) in the queue: the end where the insertion operation is performed is called Tail/Rear out of the queue: the end where the deletion operation is performed is called Head/Front
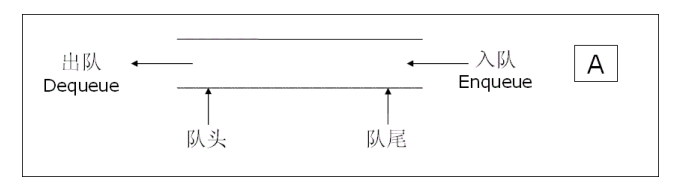
2.2 realization
The queue can also be implemented in the structure of array and linked list. It is better to use the structure of linked list, because if the structure of array is used, the efficiency will be relatively low.
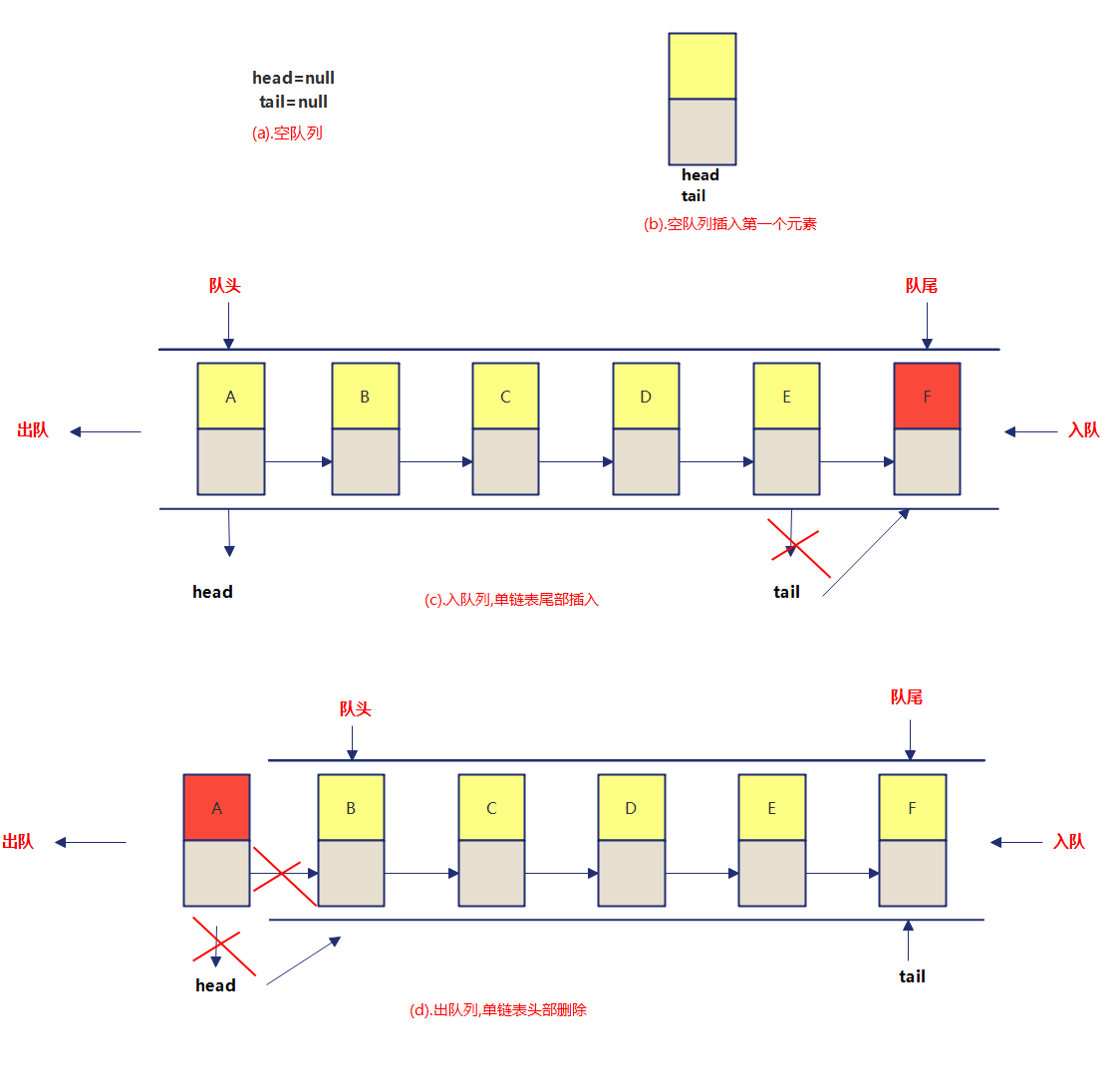
public class MyQueueByLinkedList {
/**
* Node This class is called "inner class", which defines the class in a class or method
* static The effect is that creating an instance of Node does not depend on the instance of MyQueueByLinkedList class
*/
static class Node{
public int val;
Node next = null;
public Node(int val){
this.val = val;
}
}
// To create a linked list, you must have a head node. The head node here is not a puppet node
// Based on the linked list to achieve the queue, you can enter the queue, you can insert from the tail, and the outgoing queue is deleted from the head;
// You can also insert in the queue from the head and delete out of the queue from the tail
// Either way, it's best to record the head and tail
private Node head = null;
private Node tail = null;
// Queue entry (for the queue of the standard library, the queue entry operation is called offer)
public void offer(int val) {
Node newNode = new Node(val);
if(head == null){
head = newNode;
tail = newNode;
return;
}
//If not empty
tail.next = newNode;
tail = newNode;
}
// Out of queue
public Integer poll(){
// If the current queue is empty, it is obviously unscientific to go to poll
if(head == null){
// If out of the queue fails, an error value is returned
return null;
}
int ret = head.val;
head = head.next;
if(head == null){
//After deleting the current element, the queue becomes empty
tail = null;
}
return ret;
}
// Take the first element of the team
public Integer peek() {
if(head == null){
return null;
}
return head.val;
}
}
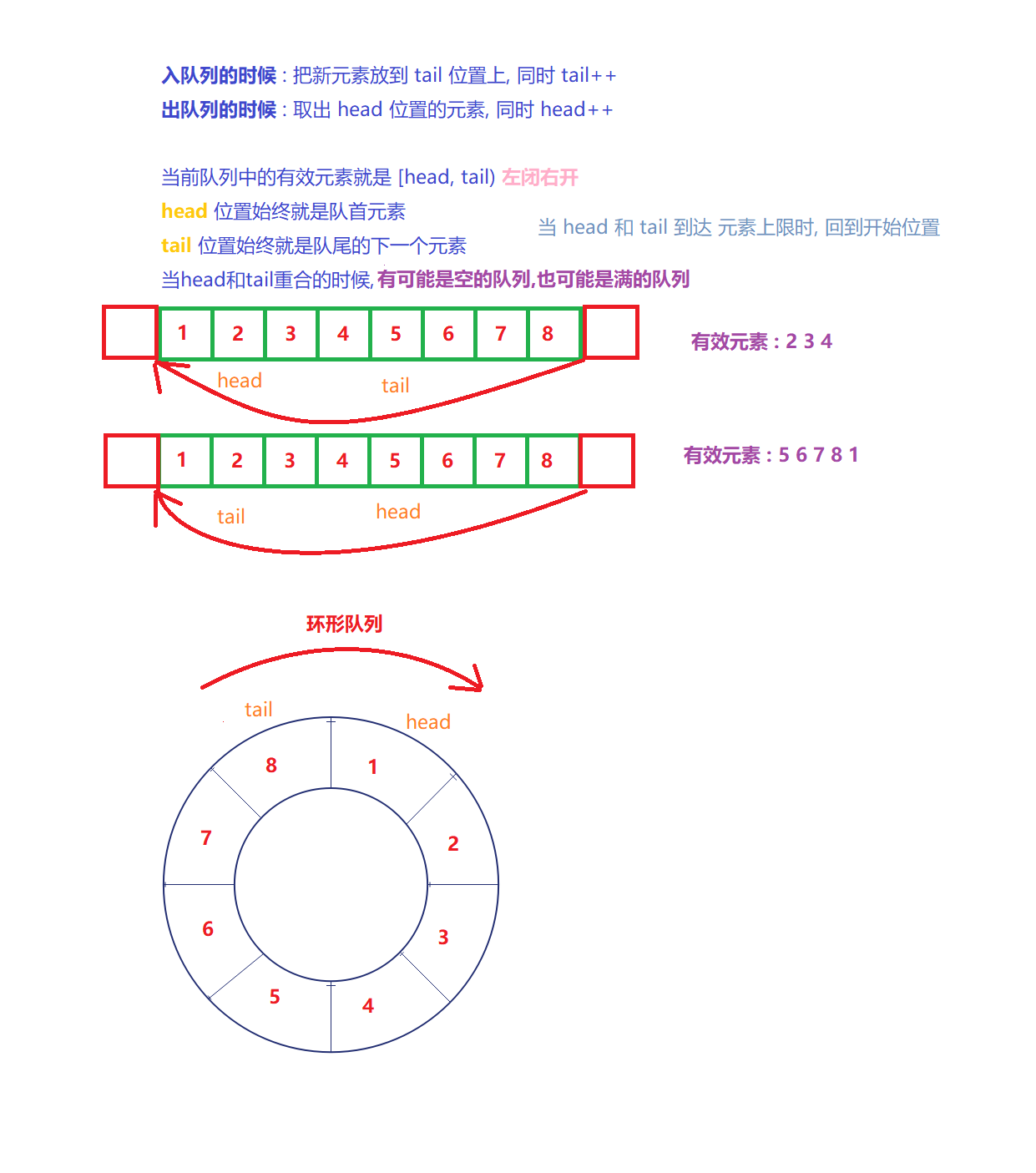
2.3 circular queue
In practice, we sometimes use a queue called circular queue. For example, circular queues can be used when the operating system course explains the producer consumer model.
Ring queues are usually implemented using arrays.
public class MyQueueByArray {
private int[] elem = new int[100];
// [head,tail) the range of valid elements. Note that tail may precede head
private int head = 0; // Indicates a subscript to the first element
private int tail = 0; // Indicates the subscript to the next element of the tail
private int size = 0; // Number of elements
public void offer(int val){
if (size == elem.length) {
//The queue is full and cannot continue inserting
return ;
}
// Ensure that the subscript of this operation cannot exceed the bounds
elem[tail] = val;
tail++;
// After tail + +, if it exceeds the valid range of the array, start from the beginning
if (tail >= elem.length){
tail = 0;
}
size++;
}
public Integer poll(){
if (size == 0){
return null;
}
Integer ret = elem[head];
head++;
if(head >= elem.length){
head = 0;
}
size--;
return ret ;
}
public Integer peek(){
if(size == 0){
return null;
}
return elem[head];
}
}
3. Dual Ended queue (Deque)
3.1 concept
**Dual ended queue (deque) * * refers to a queue that allows both ends to enter and leave the queue. Deque is the abbreviation of "double ended queue".
That means that elements can be out of the team and in the team from the head of the team, or out of the team and in the team from the end of the team.
4. Stack and queue in Java
Stack
| method | explain |
|---|---|
| E push(E item) | Stack pressing |
| E pop() | Out of stack |
| E peek() | View stack top element |
| boolean empty() | Determine whether the stack is empty |
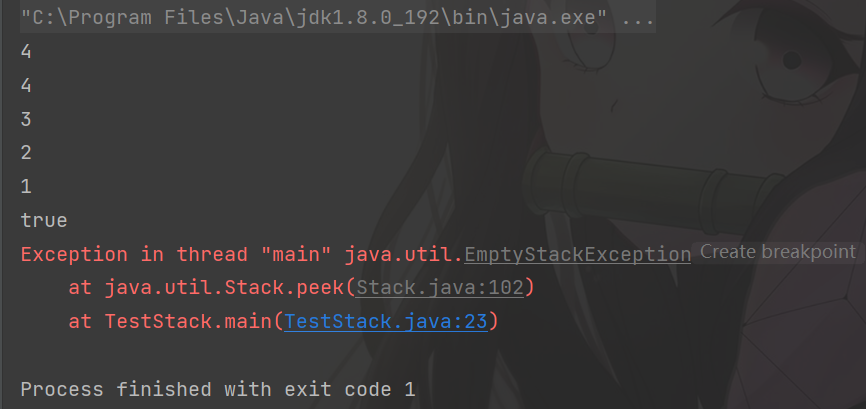
Demonstration of Stack method:
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
//Stack pressing
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
//View stack top element
System.out.println(stack.peek());
//Out of stack
int ret = stack.pop();
System.out.println(ret); //4
ret = stack.pop();
System.out.println(ret); //3
ret = stack.pop();
System.out.println(ret); //2
ret = stack.pop();
System.out.println(ret); //1
//Determine whether the stack is empty
System.out.println(stack.empty());
//At this time, the stack is empty. If you view the top element of the stack or exit the stack, an exception will be reported (emptystackeexception)
System.out.println(stack.peek());
System.out.println(stack.pop());
}
Operation results:
Queue
| error handling | Throw exception | Return special value |
|---|---|---|
| Queue | add(e) | offer(e) |
| Out of queue | remove() | poll() |
| Team leader element | element() | peek() |
Deque
| Head / tail | Head element (team leader) | Tail element (tail) | ||
|---|---|---|---|---|
| error handling | Throw exception | Return special value | Throw exception | Return special value |
| Queue | addFirst(e) | offerFirst(e) | addLast(e) | offerLast(e) |
| Out of queue | removeFirst() | pollFirst() | removeLast() | pollLast() |
| Get element | getFirst() | peekFirst() | getLast() | peekLast() |
Summary:
Stack:
Push, pop, peek. When the current stack is empty, pop or peek will generate an exception
Queue:
add,remove,element if the current operation fails, an exception will be thrown;
Offer, poll and peek will return an error value if the operation fails;
5. LeetCode topic
Question 1: valid parentheses
Valid parentheses
LeetCode 20:
Description:
Given a string s that only includes' (',') ',' {','} ',' [','] ', judge whether the string is valid.
Valid strings must meet:
- The left parenthesis must be closed with the same type of right parenthesis.
- The left parentheses must be closed in the correct order.
Problem solving ideas:
1. Traverse the string and take out the characters in the string in turn
1.1 if the extracted string is an open bracket, such as' (',' [',' {'. Put it on the stack
1.2 if the extracted string is a closing bracket, such as') ','] ','} '. Compare it with the top element of the stack to see if it matches
a) After matching, it comes out of the stack, and then continues to traverse
b) If there is no match, return false directly
1.3 if the stack is empty and the extracted character is a right parenthesis, false will be returned without the string "] ()"
2. After traversal, judge whether the stack is empty
2.1 if it is empty, the meaning of the question is satisfied. return true;
2.2 if it is not empty, it means there are not enough matching characters, return false; for example, the string "["
Drawing analysis:
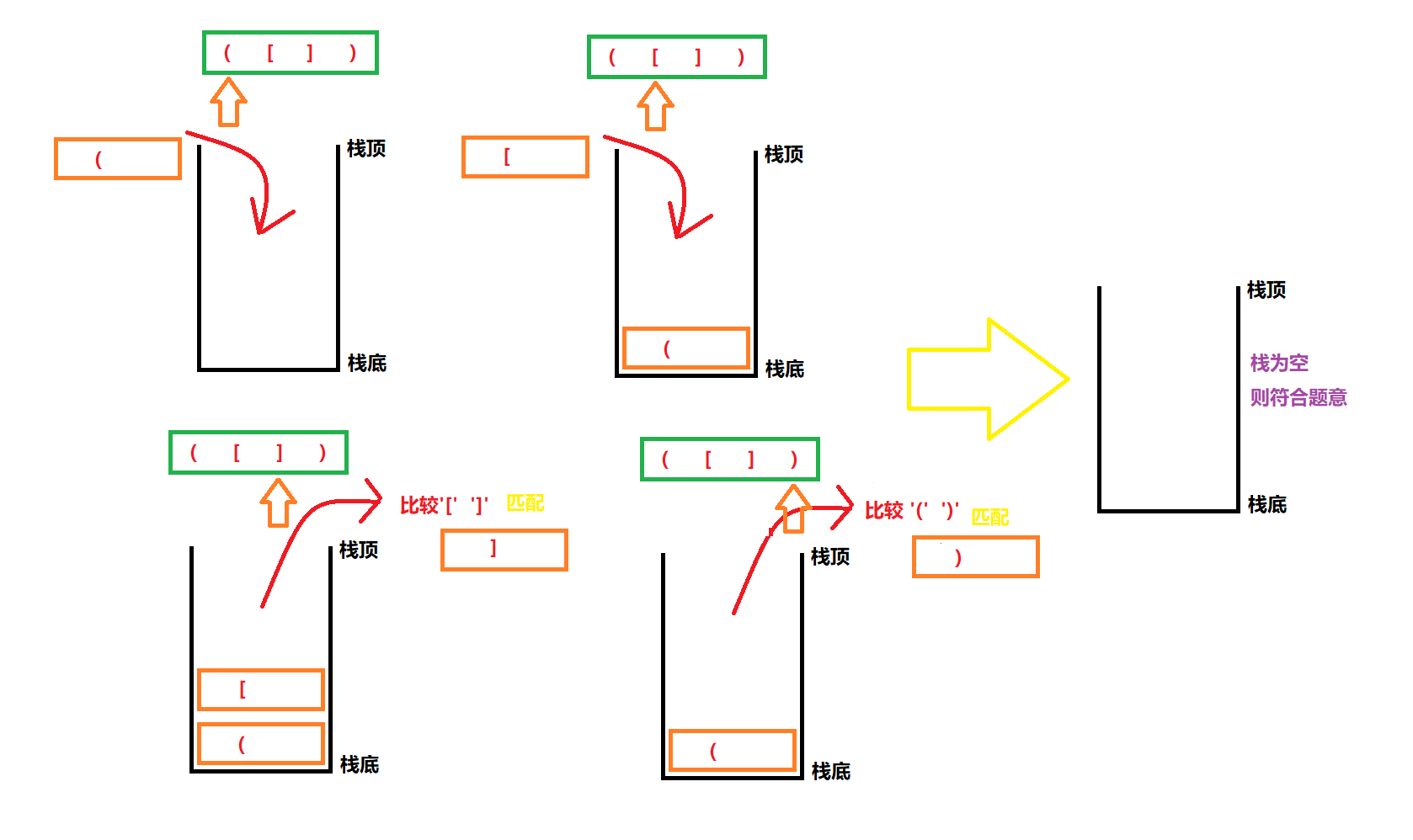
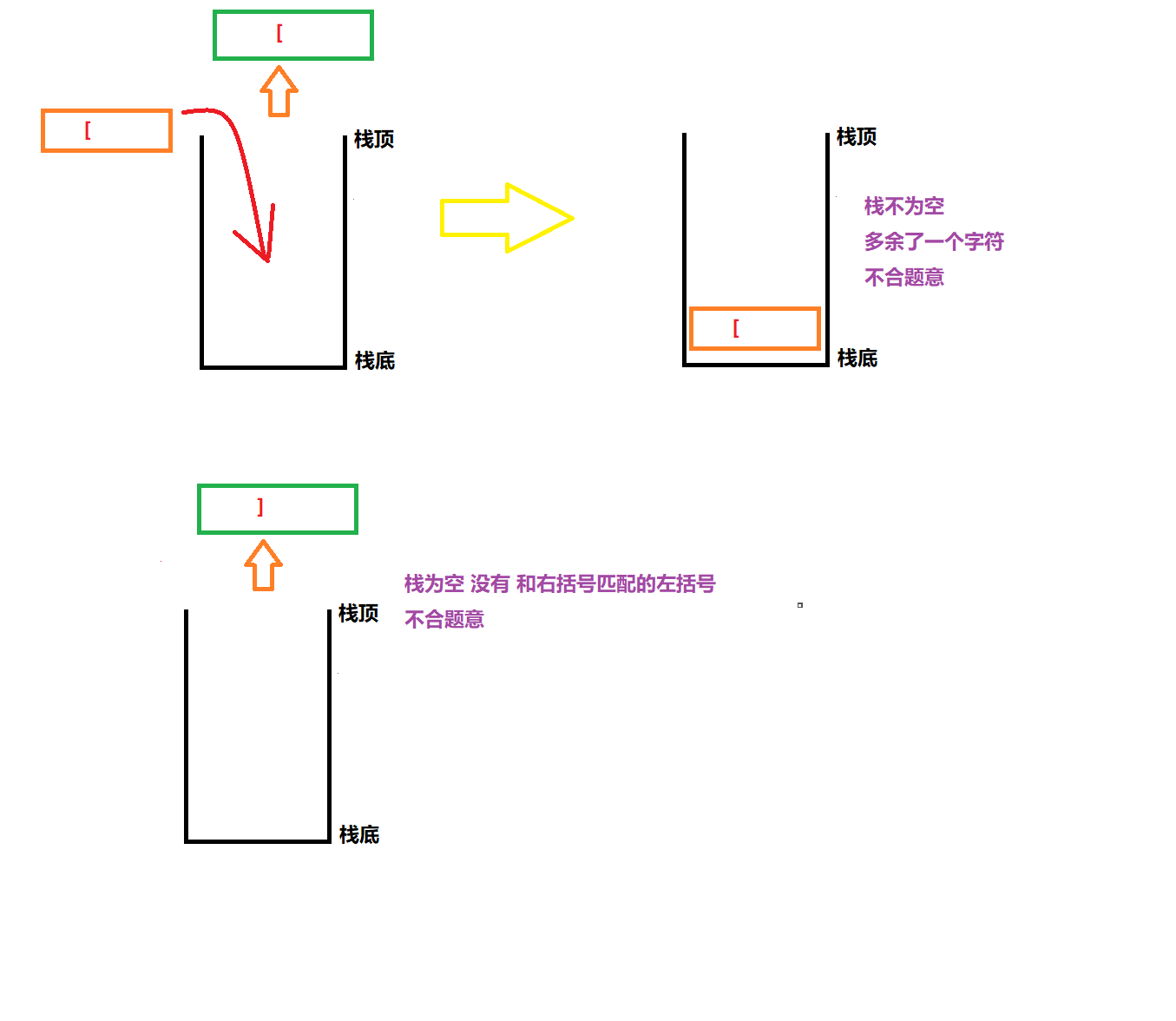
Code implementation:
public boolean isValid(String str) {
Map<Character,Character> map = new HashMap<>();
map.put('(',')');
map.put('[',']');
map.put('{','}');
//1. First create a stack and save the character type in the stack
Stack<Character> stack = new Stack<>();
//2. Traverse each character of the string
for (int i = 0; i < str.length(); i++) {
char ch = str.charAt(i);
//3. Judge whether the character ch is an open bracket. If so, put it on the stack
if (ch == '(' || ch == '[' || ch == '{'){
stack.push(ch);
continue;//Enter the next cycle and take out the next character
}
if(stack.empty()){
//If ch is not an open bracket and the stack is empty, it is not a legal bracket
return false;
}
//4. Judge whether ch is a right parenthesis. If so, take the top element of the stack and compare whether it is equal
char top = stack.pop();//Stack top element
//The following are three legal cases - write 1
/*if(top == '(' && ch == ')') {
continue;
}
if(top == '[' && ch == ']') {
continue;
}
if(top == '{' && ch == '}') {
continue;
}*/
// Judge the legal situation -- writing 2
if(map.get(top) == ch){
continue;
}
//If none of the three conditions is satisfied, it means it is not legal
return false;
}
//After traversal, if the stack is empty, the condition is met
if(stack.empty()) {
return true;
}
//Otherwise it is illegal
return false;
}
Question 2: using queue to realize stack
Implement stack with queue
LeetCode 225:
Description:
Please use only two queues to implement a last in first out (LIFO) stack, and support all four operations of the ordinary stack (push, top, pop and empty).
Implement MyStack class:
- void push(int x) pushes element X to the top of the stack.
- int pop() removes and returns the top of stack element.
- int top() returns the stack top element.
- boolean empty() returns true if the stack is empty; otherwise, returns false.
be careful:
- You can only use the basic operations of the queue -- that is, push to back, peek/pop from front, size and is empty.
- Your language may not support queues. You can use list or deque to simulate a queue, as long as it is a standard queue operation.
Problem solving ideas:
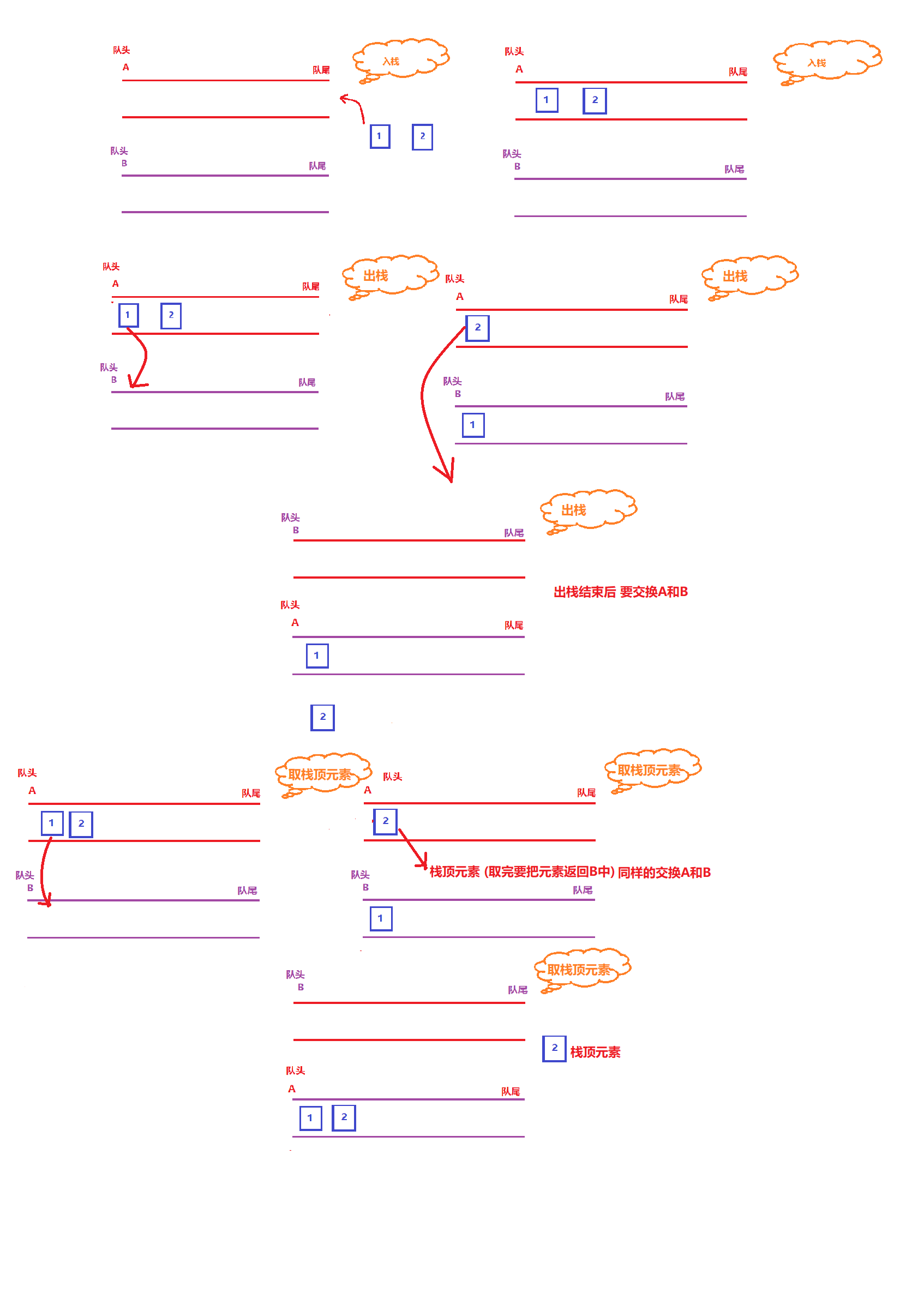
1. Use two queues to simulate the effect of A stack, and reference two queues A and B
2. Stack: directly queue the elements into A
3. Out of stack: because the queue is first in first out and the stack is last in first out, you can let the elements of queue A out of the queue and then into queue B. until the last element in queue A, you can directly out of the queue to achieve last in first out. Then you need to exchange A and B and always put them into queue A
4. Take the top element of the stack: Taking the top element of the stack is the element out of the stack, but taking the top element of the stack needs to return this element
5. Judge whether it is empty: when both A and B are empty, the stack is empty
Drawing analysis:
Code implementation:
import java.util.LinkedList;
import java.util.Queue;
public class MyStackByDoubleQueue {
private Queue<Integer> A = new LinkedList<>();
private Queue<Integer> B = new LinkedList<>();
public void push(int x) {
// x enter the queue into A
A.offer(x);
}
public Integer pop() {
if (empty()){
return null;
}
// Put the elements in A into B
while(A.size() > 1) {
Integer font = A.poll();
B.offer(font);
}
//When the loop ends, there should be only one element left in A
//This element should be the element that is out of the stack
int ret = A.poll();
//Swap A and B
swapAB();
return ret;
}
private void swapAB(){
Queue<Integer> tmp = A;
A = B;
B = tmp;
}
public Integer top() {
if (empty()){
return null;
}
// Put the elements in A into B
while(A.size() > 1) {
Integer font = A.poll();
B.offer(font);
}
//When the loop ends, there should be only one element left in A
//This element should be the element that is out of the stack
int ret = A.poll();
B.offer(ret); // The difference between top and pop is that top needs to return elements, and pop does not need to return elements
//Swap A and B
swapAB();
return ret;
}
public boolean empty() {
return A.isEmpty() && B.isEmpty();
}
}
Question 3: using stack to realize queue
Implement queue with stack
LeetCode 232:
Description:
Please use only two stacks to implement the first in first out queue. The queue should support all operations supported by the general queue (push, pop, peek, empty):
Implement MyQueue class:
- void push(int x) pushes element X to the end of the queue
- int pop() removes the element from the beginning of the queue and returns it
- int peek() returns the element at the beginning of the queue
- boolean empty() returns true if the queue is empty; Otherwise, false is returned
Problem solving ideas:
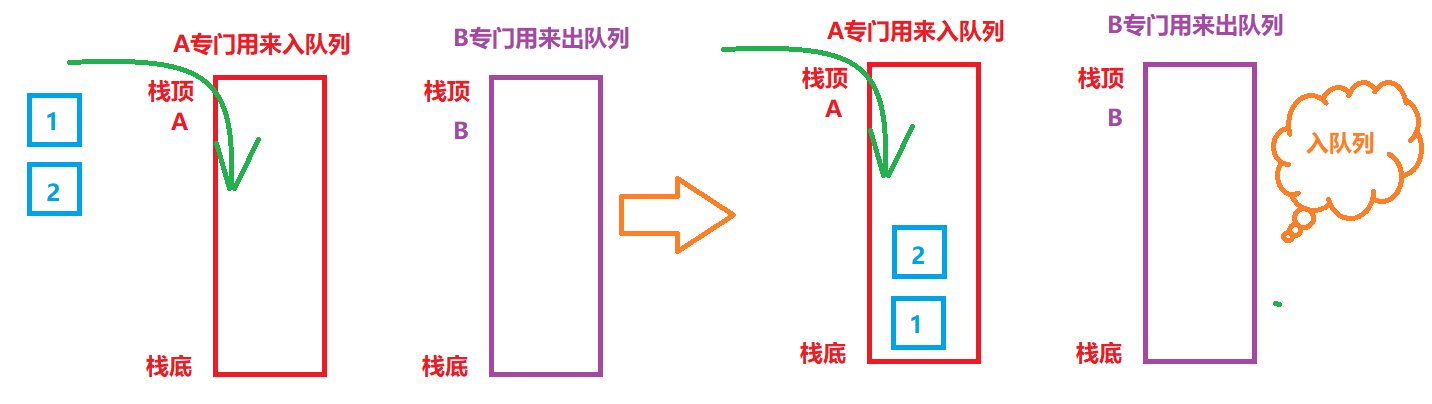
1. Reference two stacks A and B,A is used exclusively for entering the queue; B is specially used to get out of the queue
2. Implement queue entry: first put all elements in B into A (because the elements will be put into B when they are out of the stack), and then directly put them into A
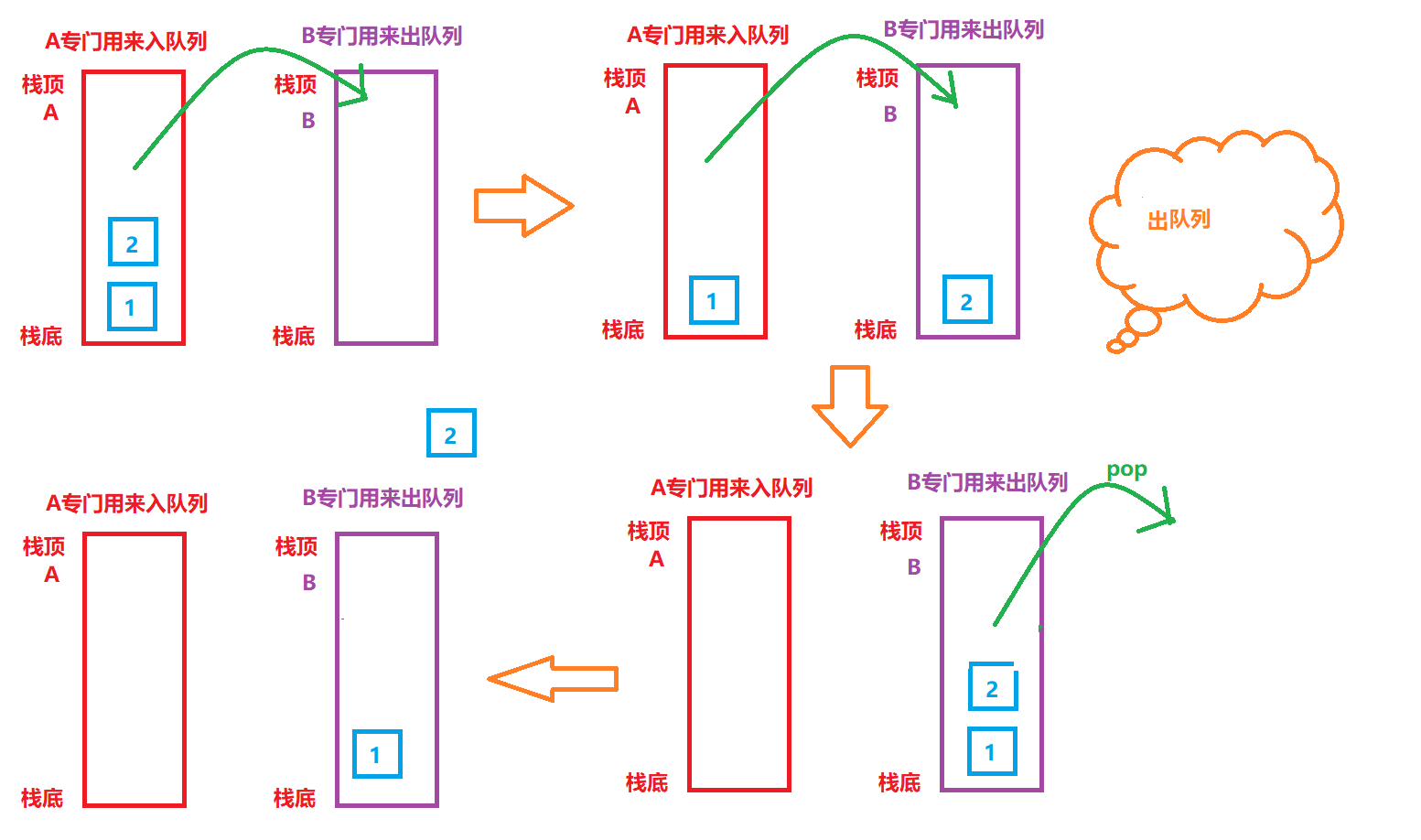
3. Implement the out of queue: the last in first out stack implements the first in first out queue. All elements in A should be moved into B. the first out element is the last in. At this time, the top of the stack is the first in element, and the out of stack operation in B is OK
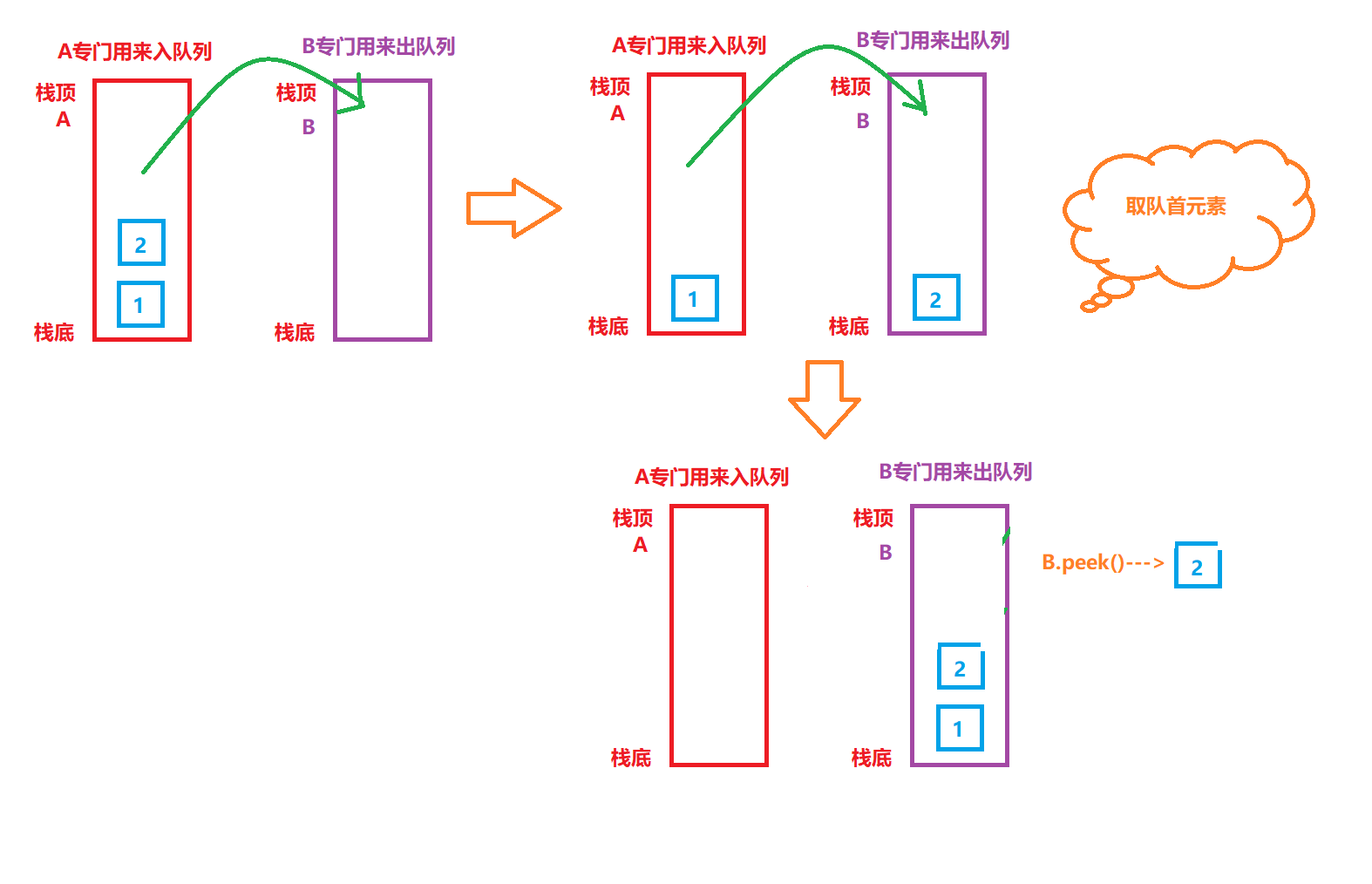
4. Get the first element of the queue: go out of the queue at the same time, put all elements of A into B, and then take the top element of B as the first element of the queue
5. Empty judgment: both A and B are empty
Drawing analysis:
Code implementation:
import java.util.Stack;
public class MyQueueByDoubleStack {
private Stack<Integer> A = new Stack<>();
private Stack<Integer> B = new Stack<>();
public void push(int x) {
//1. First put the elements in B into A
while (!B.isEmpty()){
int tmp = B.pop();
A.push(tmp);
}
//2. Put the new element into A
A.push(x);
}
public Integer pop() {
//1. If it is blank, return directly
if(empty()){
return null;
}
//2. Give all the elements in A to B
while(!A.isEmpty()){
int tmp = A.pop();
B.push(tmp);
}
//3. Stack for B
return B.pop();
}
public Integer peek() {
//1. If it is blank, return directly
if(empty()){
return null;
}
//2. Give all the elements in A to B
while(!A.isEmpty()){
int tmp = A.pop();
B.push(tmp);
}
//3. Take the stack top element of B
return B.peek();
}
public boolean empty() {
return A.isEmpty() && B.isEmpty();
}
}
Question 4: minimum stack
Minimum stack
LeetCode 155:
Design a stack that supports push, pop and top operations and can retrieve the smallest element in a constant time.
- push(x) -- pushes element x onto the stack.
- pop() -- delete the element at the top of the stack.
- top() -- get the stack top element.
- getMin() -- retrieves the smallest element in the stack.
Problem solving ideas:
1. Reference two stacks a and B. A enters and exits the stack according to the rules of normal stack, and B stores the minimum value of a and the minimum value of a history
2. Implement stack operation: in A: directly stack. In B: take the value to be stacked and compare it with the top element of B stack, and stack the smaller value into B
3. Realize stack out operation: A and B stack together
4. Realize the operation of fetching the top element of stack: directly fetch the top element of stack A
5. Realize the operation of taking the minimum value: directly take the top element of stack B
Drawing analysis:
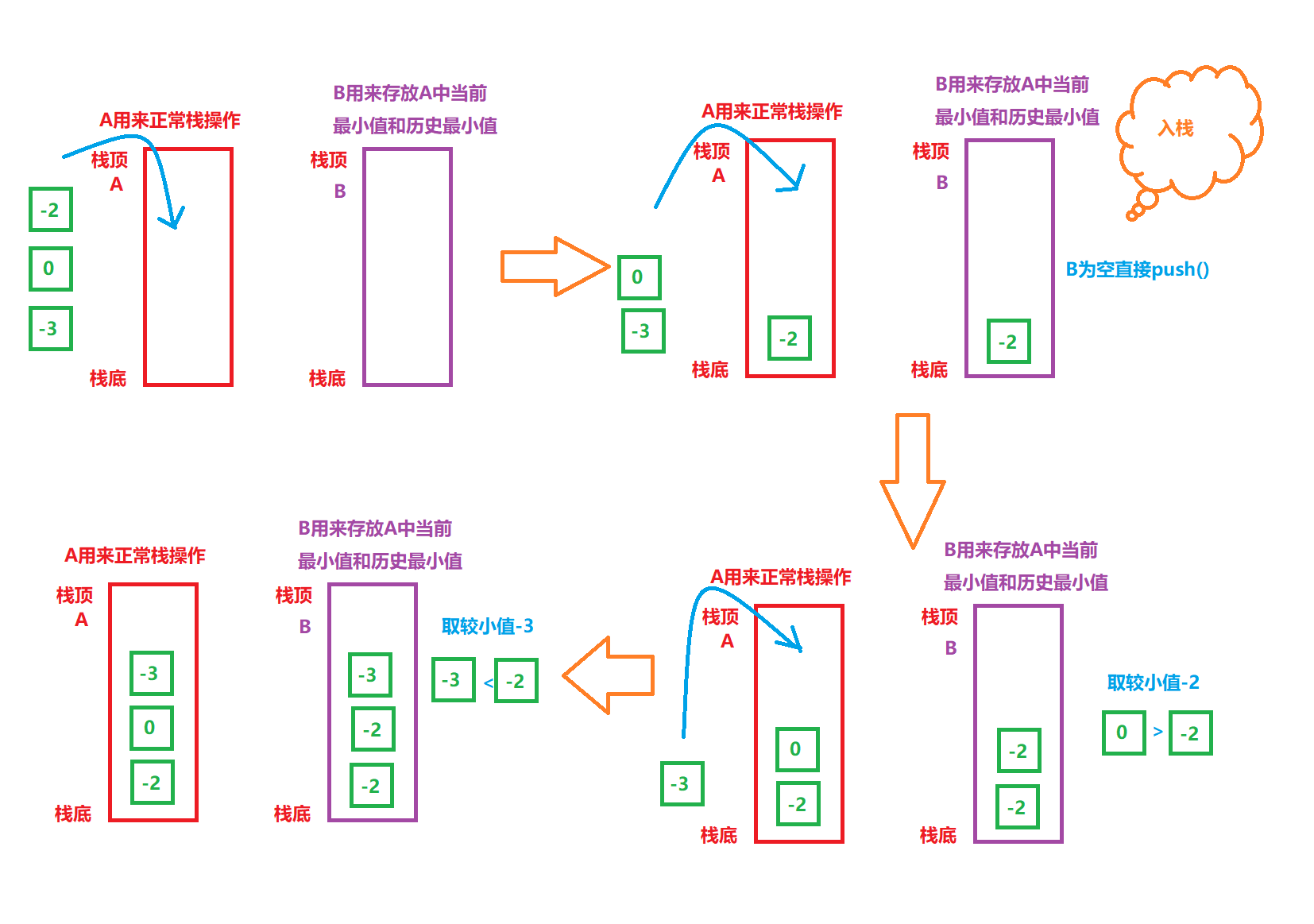
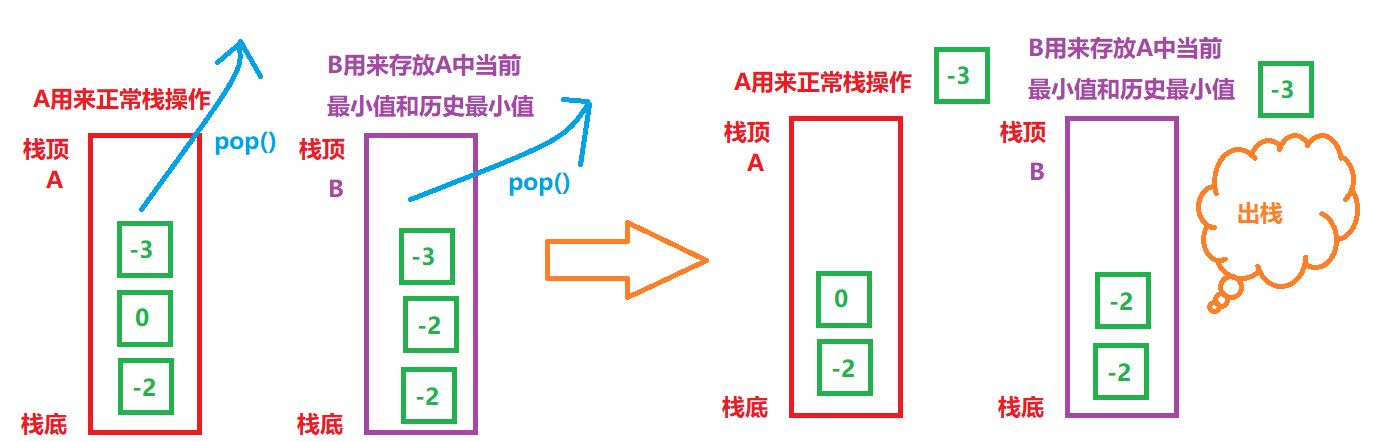
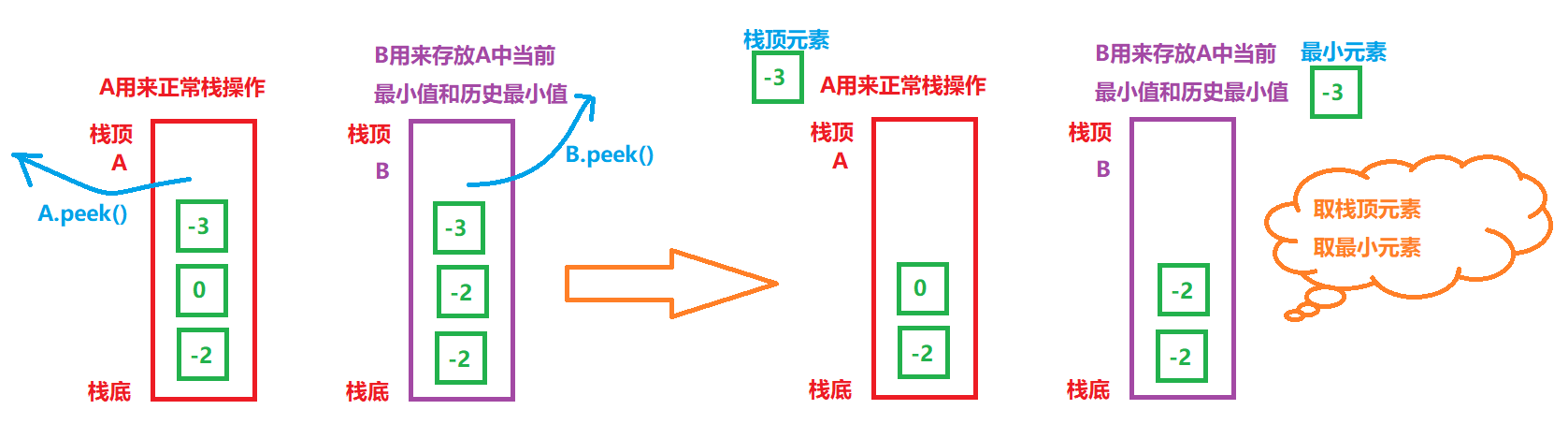
Code implementation:
import java.util.Stack;
public class MinStack {
private Stack<Integer> A = new Stack<>();
private Stack<Integer> B = new Stack<>();
public void push(int x){
//A direct stack
A.push(x);
//If B is empty, directly enter the stack
if(B.isEmpty()){
B.push(x);
return;
}
//If B is not empty, compare the smaller value at the top of x and B stack and put the smaller value on the stack
int min = B.peek();
min = min < x ? min : x;
B.push(min);
}
public Integer pop(){
//If A is empty, return directly
if(A.isEmpty()){
return null;
}
//B and A are out of the stack at the same time
B.pop();
return A.pop();
}
public Integer top(){
//If A is empty, return directly
if(A.isEmpty()){
return null;
}
return A.peek();
}
public Integer getMin(){
//If B is empty, return directly
if(B.isEmpty()){
return null;
}
//B's stack top even the smallest element
return B.peek();
}
}
Question 5: Design cyclic queue
Design cyclic queue
LeetCode 622:
Description:
Design your loop queue implementation. Cyclic queue is a linear data structure whose operation performance is based on FIFO (first in first out) principle, and the tail of the queue is connected after the head of the queue to form a loop. It is also called "ring buffer".
One advantage of the circular queue is that we can use the space previously used by the queue. In a normal queue, once a queue is full, we cannot insert the next element, even if there is still space in front of the queue. But with circular queues, we can use this space to store new values.
Your implementation should support the following operations:
- MyCircularQueue(k): constructor that sets the queue length to K.
- Front: get the element from the team leader. If the queue is empty, - 1 is returned.
- Rear: get the tail element. If the queue is empty, - 1 is returned.
- enQueue(value): inserts an element into the circular queue. Returns true if successfully inserted.
- deQueue(): deletes an element from the circular queue. Returns true if the deletion was successful.
- isEmpty(): check whether the circular queue is empty.
- isFull(): check whether the circular queue is full.
Problem solving ideas:
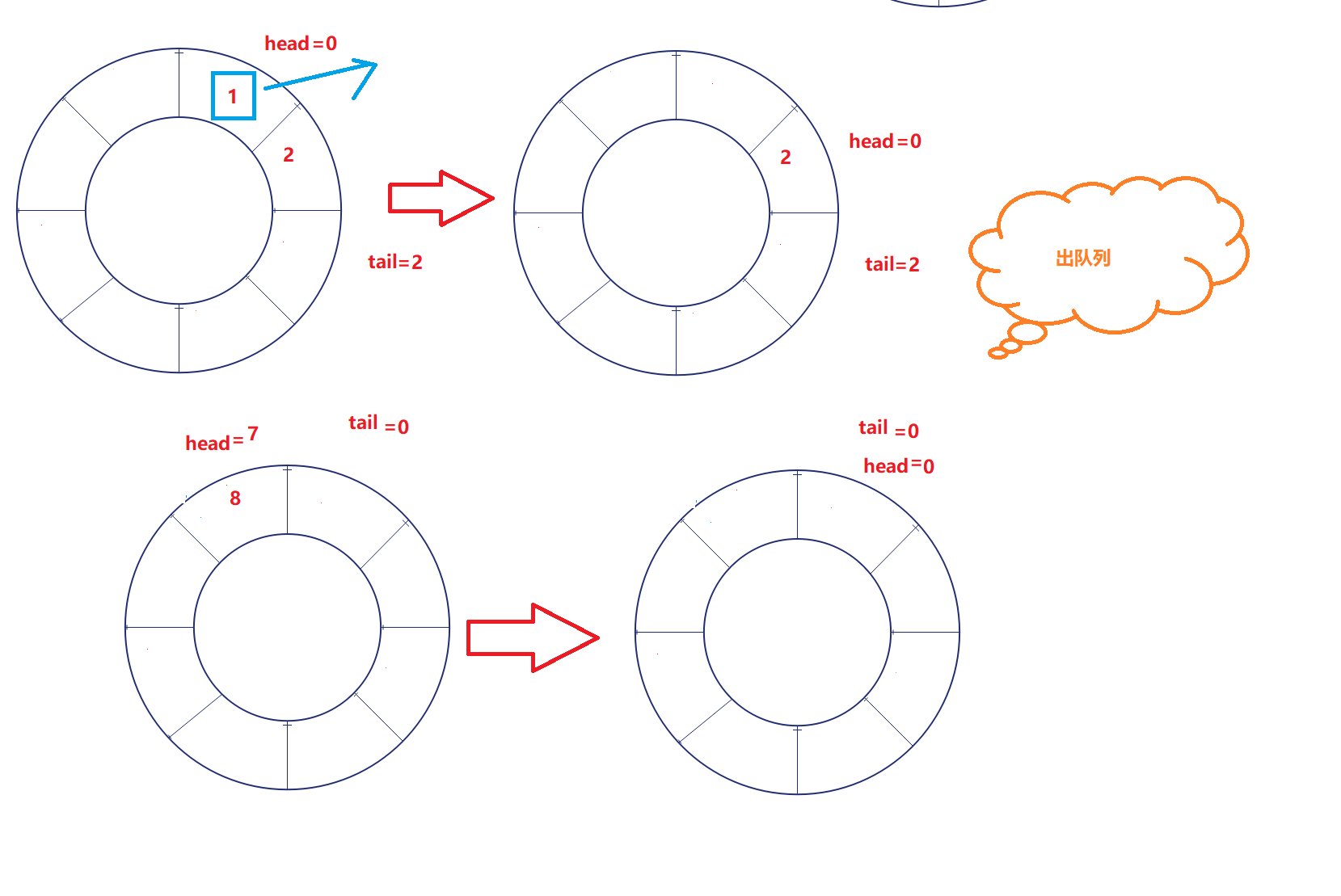
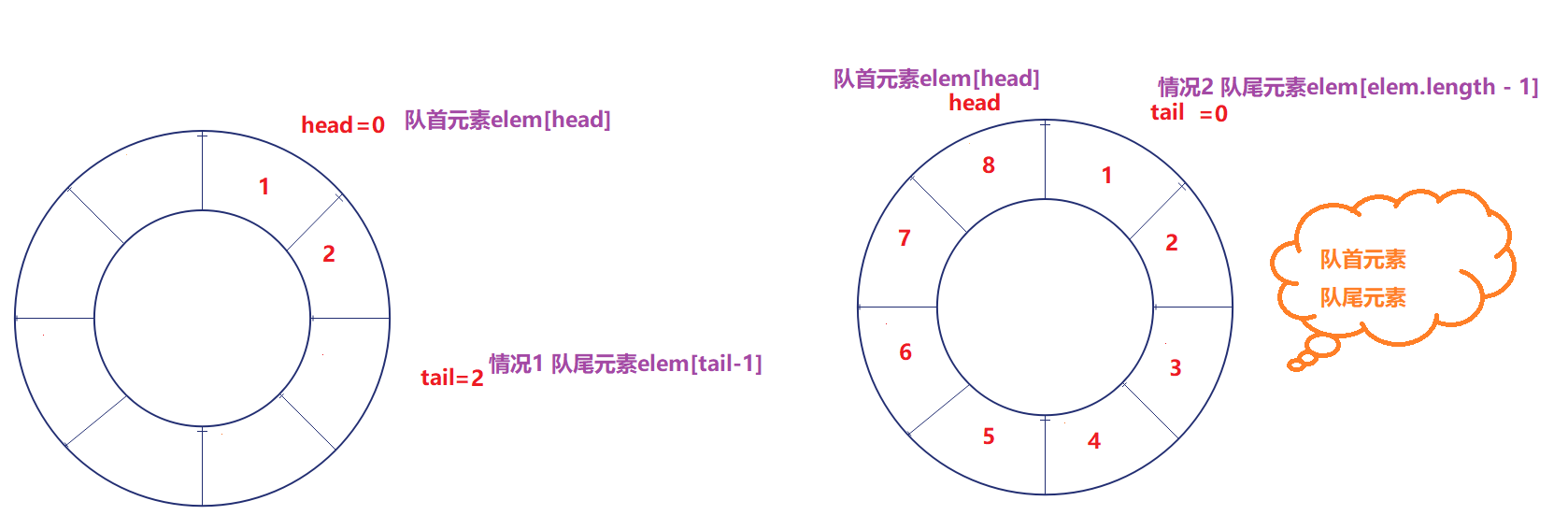
1. The circular queue is implemented by array. Head and tail are subscripts, and the head position is always the element of the head of the queue; The tail position is always the next element at the end of the queue. The number of effective elements [head, tail) is closed left and open right
2. Enter the queue: put the new element in the tail position and the tail + +
3. Out of the queue: take out the element at the head position and add head + +
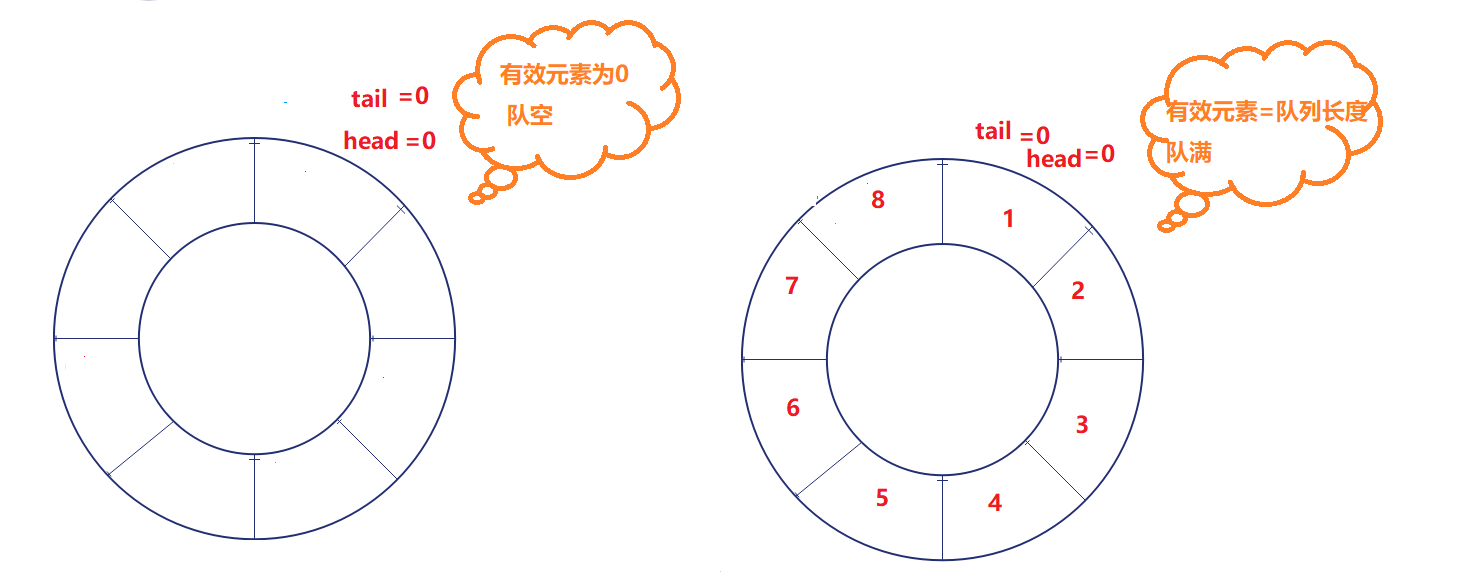
4. Empty queue: 0 valid elements
5. Full queue: the number of effective elements is equal to the length of the array
6. Note that when the head and tail reach the element line, they return to the initial position
Drawing analysis:
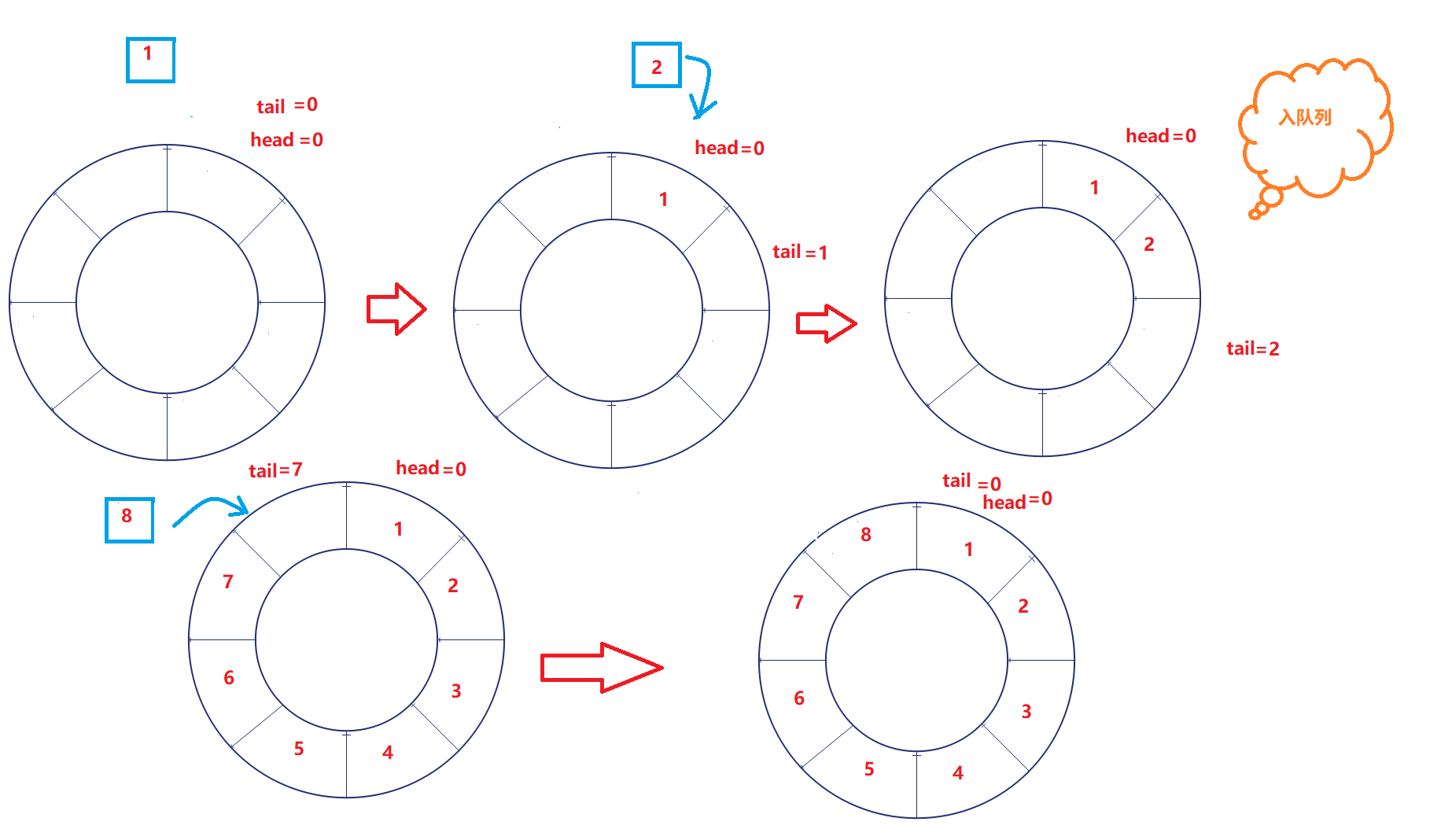
Code implementation:
public class MyCircularQueue {
private int[] elem;
private int head = 0;//Header element subscript
private int tail = 0;//Subscript of the next element at the end of the queue
private int size = 0;//Number of valid elements
/**
* Constructor, set the queue length to k.
* @param k queue length
*/
public MyCircularQueue(int k) {
this.elem = new int[k];
}
/**
* Inserts an element into the circular queue. Returns true if the insertion was successful.
* @param value Insert element
* @return
*/
public boolean enQueue(int value) {
//If the team is full, you can't join the team. Return false
if(size == elem.length){
return false;
}
elem[tail] = value;
tail++;
//Tail > = the queue length should be reset to zero
if(tail >= elem.length){
tail = 0;
}
size++;
return true;
}
/**
* Deletes an element from the circular queue. Returns true if the deletion was successful.
* Team leader
* @return
*/
public boolean deQueue() {
//If the queue is empty and there is no to delete, false is returned
if(size == 0){
return false;
}
head++;
//Head > = the queue length should be set to zero
if(head >= elem.length){
head = 0;
}
size--;
return true;
}
/**
* Gets the element from the queue head. Returns - 1 if the queue is empty.
* @return
*/
public int Front() {
if(size == 0){
return -1;
}
return elem[head];
}
/**
* Gets the end of queue element. Returns - 1 if the queue is empty.
* @return
*/
public int Rear() {
if(size == 0){
return - 1;
}
if(tail==0) return elem[elem.length - 1];
return elem[tail-1];
}
/**
* Check whether the circular queue is empty.
* @return
*/
public boolean isEmpty() {
if(size == 0){
return true;
}
return false;
}
/**
* Check if the circular queue is full
* @return
*/
public boolean isFull() {
if(size == elem.length){
return true;
}
return false;
}
}
Question 6: evaluation of inverse Polish expression (suffix expression)
Postfix Expression
Inverse Polish expression evaluation
LeetCode 150:
Sword finger Offer Ⅱ 036:
Description:
Find the value of the expression according to the inverse Polish representation.
Valid operators include +, -, *, /. Each operand can be an integer or another inverse expression.
explain:
Integer division preserves only the integer part.
A given inverse Polish expression is always valid. In other words, the expression always yields a valid value and there is no case where the divisor is 0.
Problem solving ideas:
- Infix notation is a general expression of arithmetic or logic formula, such as 3 + 4
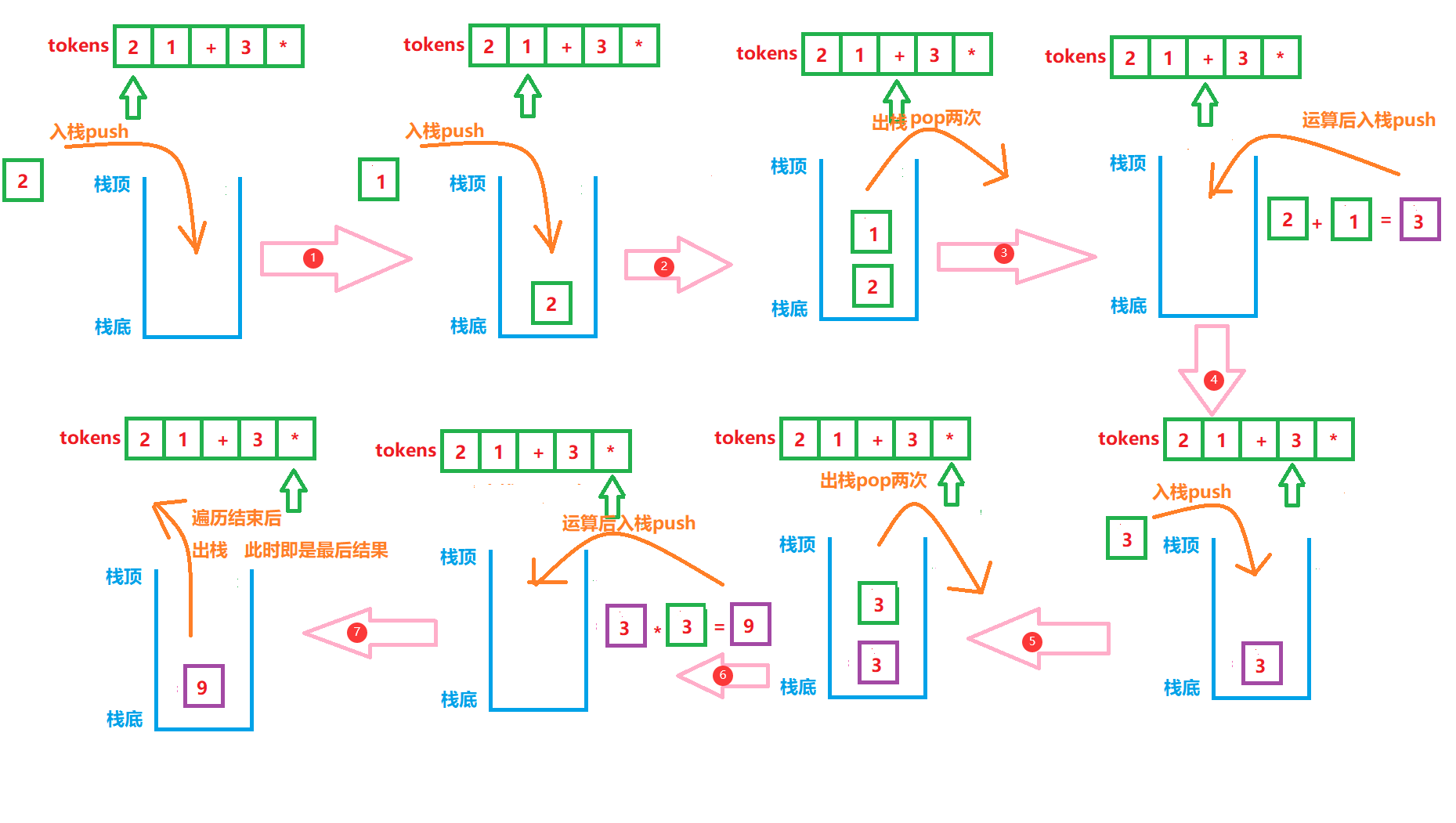
Prefix expressions such as + 3 and 4, and suffix expressions such as 3 and 4 +. Both prefix and suffix expressions represent 3 + 4 - Use the stack to solve the inverse Polish expression and traverse the character array
① If it is a number
② If it is +, -, *, / out of the stack, complete the corresponding operation, and then put the obtained data into the stack - Note that when the corresponding +, -, *, / operations are completed, it is the data of the last stack +, -, *, / and the data of the previous stack
Drawing analysis:
Code implementation:
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
int sum = 0;
//ergodic
for (int i = 0; i < tokens.length; i++) {
if("+".equals(tokens[i])){
// '+' operation
stack.push(stack.pop() + stack.pop());
}else if ("-".equals(tokens[i])){
// '-' operation
stack.push(-stack.pop() + stack.pop());
}else if ("/".equals(tokens[i])){
// '/' operation
int m = stack.pop();
int n = stack.pop();
stack.push(n / m);
}else if ("*".equals(tokens[i])){
// '*' operation
stack.push(stack.pop() * stack.pop());
}else{
// Not an operator directly on the stack
stack.push(Integer.valueOf(tokens[i]));
}
}
//After traversal, the stack is the result
return stack.pop();
}