
Welcome back to: meet blue bridge, meet you, not negative code, not negative Qing!
catalogue
Chestnut 3: the middle node of the linked list
Chestnut IV: circular linked list
Chestnut five: circular linked list II
Chestnut six: the penultimate node of the linked list
4, Blue bridge conclusion: meet blue bridge meet you, not negative code, not negative Qing!
[preface]
There are three chapters in the basic part of the blue bridge cup that will be updated. Then the author will prepare for the final exam. When the winter vacation comes, he will start the blue bridge sprint column before the exam. There are dry goods, much more than here! So what we need to do now is to thoroughly understand the basic knowledge points. Remember, those who succeed early may not succeed, and those who arrive late may not fail! So come on, boy.

1, What are two pointers
Double pointer is a very important idea in algorithm programming, but few textbooks speak it alone. One of the reasons is that it prefers a programming skill and doesn't look like an "algorithm". The idea of double pointer is very concise, but it provides very high algorithm efficiency.
There are three types of double pointers:
Ordinary pointer: two pointers move in the same direction;
Colliding pointers (mostly used in the case of order): two pointers move face to face (for example, one end moves to the middle);
Fast and slow pointer: slow pointer + fast pointer.
Note: most of the questions are collision pointers and fast and slow pointers, but don't worry about iron juice. There are a large number of classic questions behind, which are enough to let you firmly grasp two pointers!
2, Chestnut introduction
Title: given an ordered array (the array is incremented), such as array arr = {1,4,5,7,9}; Find the sum of the two numbers as 12 and find a group to stop.
[method 1]:
Obviously, it is very simple to use violence to solve this problem. It is solved directly by applying two-level cycle, but the time complexity must be O(N^2), which is very inefficient. So it's not advisable!
Violence Code:
for (i = 0; i < n; i++)
{
for (j = 1; j < n; j++)
{
if (arr[i] + arr[j] == k)
{
printf("%d %d\n", arr[i], arr[j]);
}
}
}[method 2]:
This problem is already an ordered array, so we can use "colliding pointers" to solve it.
Idea:
Note that i and j in this question are not brainless + + - Oh, it's a bit similar to the feeling of binary search. i don't believe you see.

Code execution:
#include<stdio.h>
int main()
{
int arr[] = { 1,4,5,7,9 };
int sz = sizeof(arr) / sizeof(arr[0]);
int k = 12;
int i = 0;//i start from scratch
int j = sz - 1;//j start from tail
while (i < j)
{
if (arr[i] + arr[j] < k)
{
i++;
}
else if (arr[i] + arr[j] > k)
{
j--;
}
else
{
printf("%d %d\n", arr[i], arr[j]);
break;
}
}
return 0;
}This solution is very simple. The time complexity can be controlled to O(N) with a little change, so we need to master it! OK, here are some hard dishes. They are all practical classics!

3, Force buckle classic
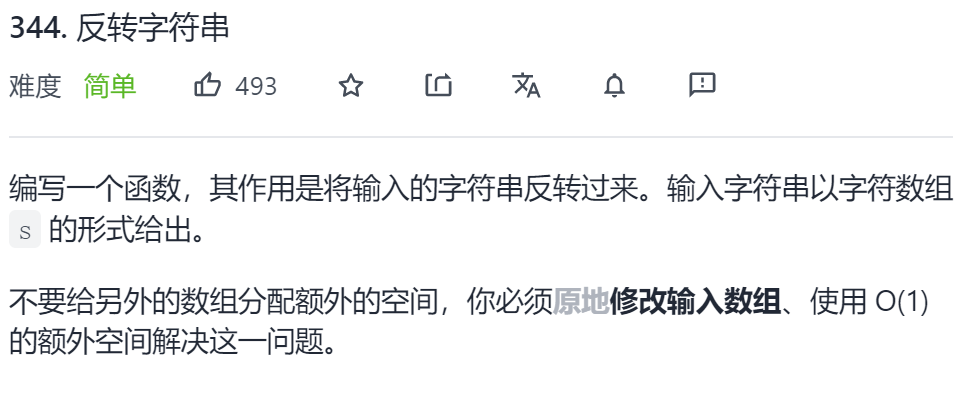
Chestnut 1: reverse string
Original title link: Force buckle
Title Description:
Example:
Input: s = ["h","e","l","l","o"] Output:["o","l","l","e","h"]
Train of thought (collision pointer):
Using the "collision pointer", one from the beginning and one from the end, the exchange is over, so easy!
Code execution:
void reverseString(char* s, int sSize){
char* left = s;//Point to start address
char* right = s + sSize - 1;//Point to last address
while(left < right)//When left > = right, there is no need to exchange
{
char* temp = *left;
*left = *right;
*right = temp;
left++;
right--;
}
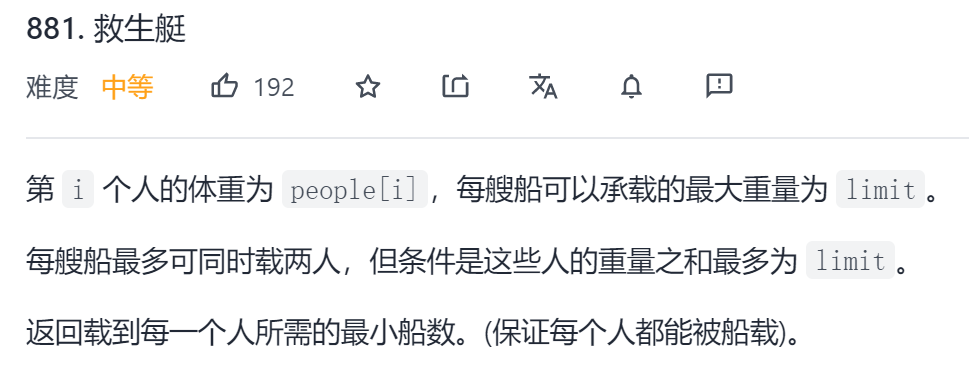
}Chestnut II: lifeboat
Original title link: Force buckle
Title Description:
Example 1:
Input: people = [1,2], limit = 3 Output: 1 Explanation: 1 ship (1, 2)
Example 2:
Input: people = [3,2,2,1], limit = 3 Output: 3 Explanation: three ships carry (1, 2), (2) and (3)
Train of thought (collision pointer):
This topic is similar to the introduction of chestnuts above. It also adopts the idea of "collision pointer", but this topic is not ordered at the beginning, so it is sorted first. The code is written in C + +. Because STL can be used, there is no need to write a sorting algorithm artificially, which is very convenient.

Code execution:
class Solution {
public:
int numRescueBoats(vector<int>& people, int limit) {
//Sort array first
sort(people.begin(),people.end());
int i = 0;//Starting position
int j = people.size() - 1;//End position
int count = 0;
while(i <= j)
{
if(people[i]+people[j] <= limit)//i is special. Imagine where it is
{
i++;
}
j--;
count++;
}
return count;
}
};OK, there are "collision pointers" in front, but in practical application, including the written examination and interview, the "fast and slow pointer method" often appears, but don't worry, there are four questions behind to feel its wonderful sound.

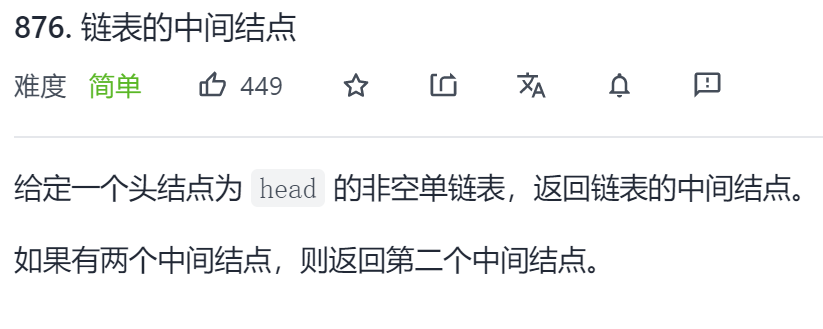
Chestnut 3: the middle node of the linked list
Original title link: Force buckle
Title Description:
Example 1:
Input:[1,2,3,4,5] Output: node 3 in this list (Serialization form:[3,4,5]) The returned node value is 3. (The serialization expression of this node in the evaluation system is [3,4,5]). Notice that we returned a ListNode Object of type ans,So: ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, as well as ans.next.next.next = NULL.
Example 2:
Input:[1,2,3,4,5,6] Output: node 4 in this list (Serialization form:[4,5,6]) Since the list has two intermediate nodes with values of 3 and 4, we return the second node.
Train of thought (speed pointer):
This topic adopts "fast and slow pointer" Solution: the slow pointer takes one step at a time and the fast pointer takes two steps at a time. However, it should be noted that this problem is affected by the fact that the total number of nodes is odd. When the total number of nodes is odd, fast - > next = = null, slow points to the intermediate node; when the total number of nodes is even, fast == NULL, slow points to the intermediate node, so there are two cycle conditions, but the sequence of cycle conditions is different The order is also exquisite. I don't believe you look at the code.
Code execution:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* middleNode(struct ListNode* head){
//Both pointers start from scratch
struct ListNode* slow = head;
struct ListNode* fast = head;
//Note that the loop condition cannot be written in the form of fast - > next & & fast, because fast may point to null after two steps
//Executing the loop condition fast - > next again will lead to null pointer exception and out of bounds, but the above situation will not occur if fast is written in front, because && there is short-circuit evaluation
while(fast && fast->next)
{
slow = slow->next;//slow one step at a time
fast = fast->next->next;//fast takes two steps at a time
}
return slow;//At this point, slow points to the intermediate node
}Chestnut IV: circular linked list
Original title link: Force buckle
Title Description: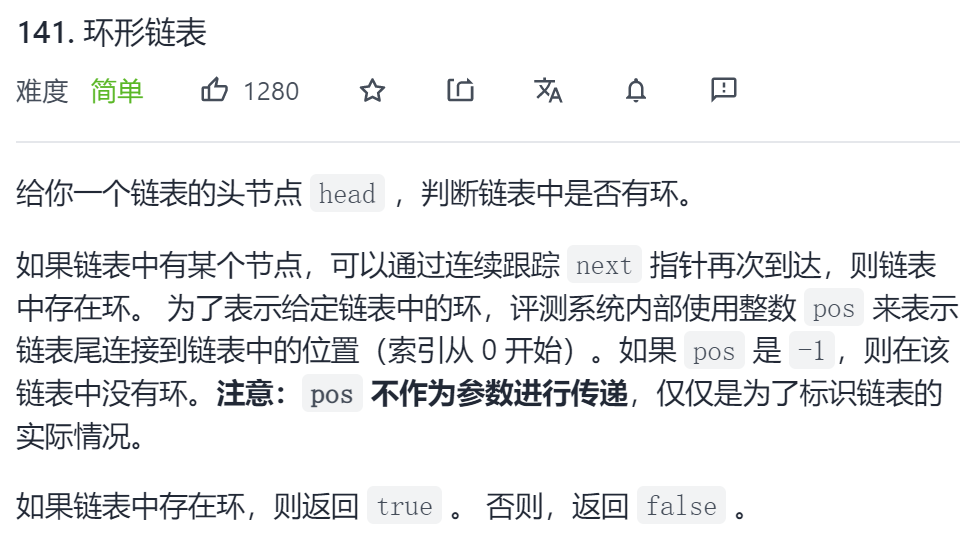
Example 1:
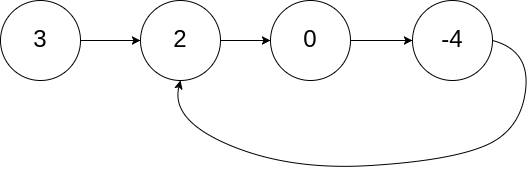
Input: head = [3,2,0,-4], pos = 1 Output: true Explanation: there is a ring in the linked list, and its tail is connected to the second node.
Example 2:

Input: head = [1], pos = -1 Output: false Explanation: there are no links in the linked list.
Train of thought (speed pointer):
Very simple, use the speed pointer to do it. If the linked list has rings, slow and fast will meet.
Code execution:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool hasCycle(struct ListNode *head) {
struct ListNode* slow = head;
struct ListNode* fast = head;
Add here fast->next The purpose is to prevent null pointer exceptions because the loop body fast Take two steps at a time
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
return true;
}
}
return false;
}Chestnut five: circular linked list II
Original title link: Force buckle
Title Description:
Example 1:
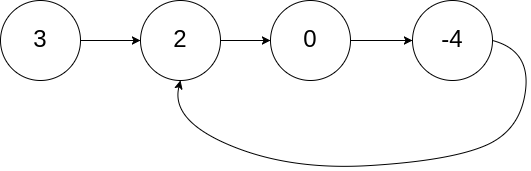
Input: head = [3,2,0,-4], pos = 1 Output: returns the linked list node with index 1 Explanation: there is a ring in the linked list, and its tail is connected to the second node.
Example 2:
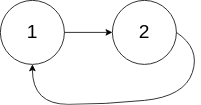
Input: head = [1,2], pos = 0 Output: returns the linked list node with index 0 Explanation: there is a ring in the linked list, and its tail is connected to the first node.
Train of thought (speed pointer):
This topic is difficult to understand, so the author specially drew it, good health.
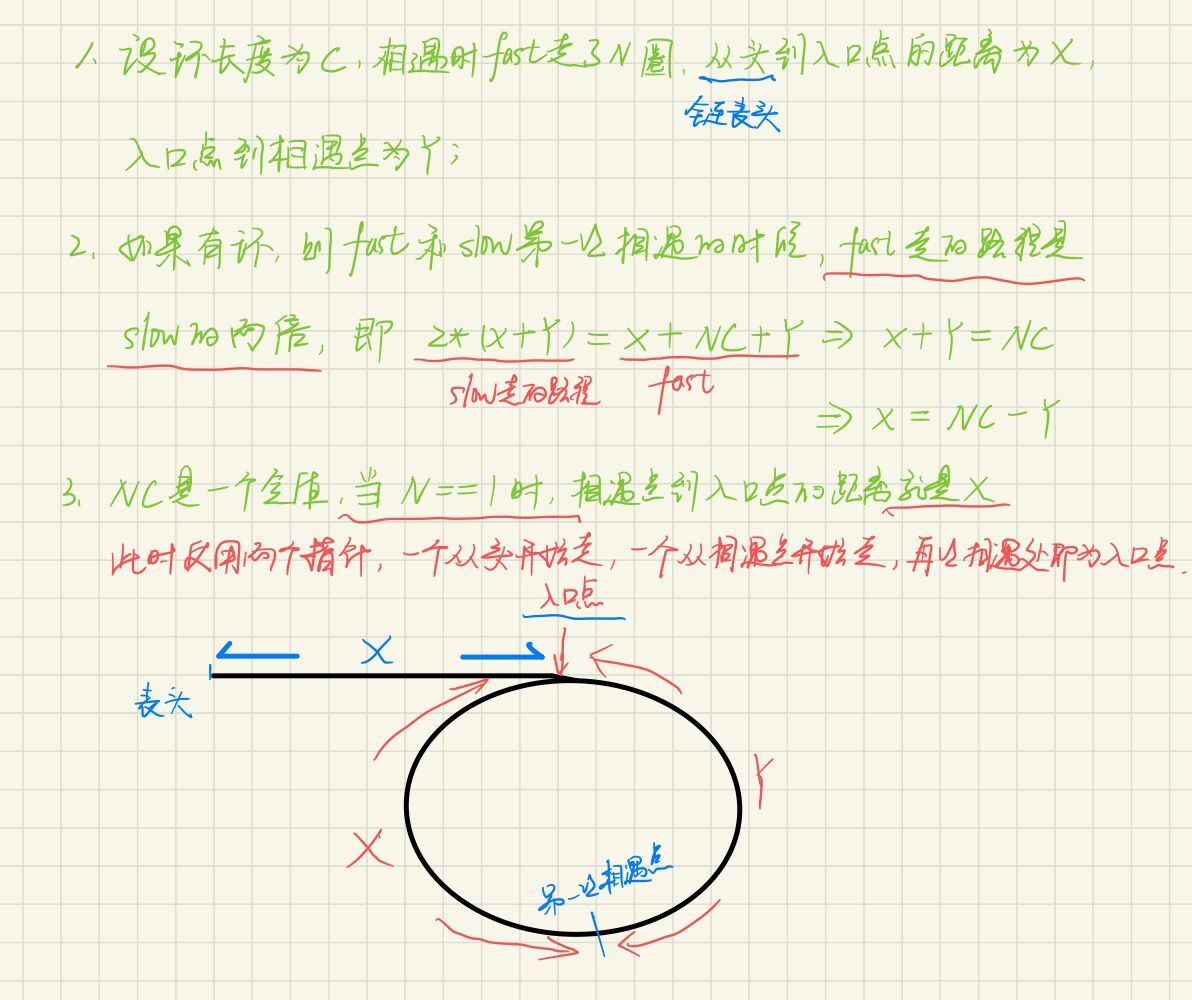
Code execution:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode* slow = head;
struct ListNode* fast = head;
while(fast && fast->next)//Find the first meeting point first
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
break;
}
}
//When the linked list has no rings, if there are rings, there must be no NULL
if(fast == NULL || fast->next == NULL)
{
return NULL;
}
//After meeting, there is a ring. At this time, use two pointers, one from the beginning
//One starts from the meeting point, and the place where the two meet again is the entry point
slow = head;
while(slow != fast)
{
slow = slow->next;
fast = fast->next;
}
return slow;
}Chestnut six: the penultimate node of the linked list
Original title link: https://leetcode-cn.com/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/
Title Description:
 Example:
Example:
Given a linked list: 1->2->3->4->5, and k = 2. Return to linked list 4->5.
Train of thought (speed pointer):
Let fast take k steps first, and then fast and slow go together. It's relatively simple. I wrote this question last time, so I directly upload the JAVA code.
Code execution:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
//When the single linked list is empty
if(head == null) {
return null;
}
//To judge the validity of K, in order to traverse the linked list again and again to solve the problem, the condition of k > size () is not added
if(k <= 0) {
return null;
}
//Using the speed pointer, fast takes the k-1 step first. Note that k > size () should be prevented here
ListNode fast = head;
ListNode slow = head;
while(k -1 > 0) {
if(fast.next != null) {
fast = fast.next;
k--;
}else {
return null;
}
}
//At this point, fast and slow go together
while(fast.next != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
4, Blue bridge conclusion: meet blue bridge meet you, not negative code, not negative Qing!
There are about three chapters left in the basic part of the blue bridge. The author is working overtime to sort it out. Because the final exam is coming soon, it may affect the progress, but it will squeeze time to update. The support of iron juice is my biggest driving force. I beg for Sanlian duck.
