<. Shape of tree: [Left subtree (left interval)] Root (parent node) [Right subtree (right interval)]
Pickle Why traverse is continuously climbing down the left subtree to the next level~~in order to reach the first node in the current layer.
Pickle For tree traversal, to the next level, formally comes first to the root (parent node).
1. Binary Tree Universal Interface [Traverse]:
<. Pre-order traversal: Root (parent) Left Subtree Right Subtree | Root (parent) Right Subtree Left Subtree [Preorder only needs root first access]
<. Mid-order traversal: left subtree Root (parent) Right Subtree | Right Subtree Root (parent) Left Subtree [Intermediate order only needs root intermediate access]
<. Post-order traversal: Left Subtree Right Subtree Root (parent) | Right Subtree Left Subtree Root (parent) [Succession only requires root last access]
<. Sequence traversal: Layer-by-layer nodes are accessed from left to right.
Pickle Common interface for binary trees:
Traversal [Pre, Medium, Post, Sequence, Elements (Design Interfaces) + Enhanced Traverse] + Front-drive, Back-drive Node+ Tree Depth + Is it a complete binary tree
1, Preorder traversal:
Recursion: around the root
Iteration: [Use stack]: Continue to the next level [via node.left method]: Continue to get the root of the next level, add the root data,
Until you reach the last level [node.left = null], pop out the current root node and switch to the right subtree through it.
_Pre-traversed code:
//Recursive implementation
// Pre-order traversal requires an incoming node (root node) before it can begin
private void preorderTraversal(Node<E> node) {
// Continuously traverse and end when you have time
if (node == null)
return;
System.out.println(node.elmement);
preorderTraversal(node.left);
preorderTraversal(node.right);
}//Iterate implementation [and store results in a List]
public List<Integer> preorderTraversal1(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
//The traversed points do not need to be able to pop() off and keep pop() until you get the right node of the current node (first, the continuously updated node is the left node)
//Then there is no left node, start pop() one layer (one node)
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
while (node != null) {
res.add(node.val);
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
return res;
}2, Intermediate traversal:
Recursion: left root right
Iteration: [Use stack]: Continue to the next level [via node.left method]: Continue to get to the root of the next level,
Until you reach the last level [node.left = null], pop out the current root node, add data from the current root, and switch it to the right subtree.
_Code traversed in middle order:
// Recursion:
private void inorderTraversal(Node<E> node) {
if (node == null)
return;
inorderTraversal(node.left);
System.out.println(node.elmement);
inorderTraversal(node.right);
} // iteration
public List<Integer> inorderTraversal2(TreeNode root) {
List<Integer> list2 = new ArrayList<>();
if (root == null)
return list2;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode node = root;
while(node != null || !stack.isEmpty() ) {
while(node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
list2.add(node.val); //You have reached the current node
node = node.right;
}
return list2;
}3, followed by traversal:
Recursion: Left and Right Roots
Iteration: [Use stack]: Continue to the next level [via node.left method]: Continue to get to the root of the next level,
Until you reach the last level [node.left = null], pop out the current root node, considering the right node: [Situation 1: The right node exists, push the root back, switch to the right subtree]
[Scenario 2: The right node does not exist or the right node of the current node is the last traversed node, which adds the data of the current node (root) and records the previous node.)
Post-traversal code:
// Recursion:
private void postorderTraversal(Node<E> node) {
if (node == null)
return;
postorderTraversal(node.left);
postorderTraversal(node.right);
System.out.println(node.elmement);
} // iteration
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root == null) return list;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode prev = null;
while(!stack.isEmpty() || root != null) {
while(root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
//Consider Right Node
//The right node does not exist, or the right node is the prev of the previous traversed node
if (root.right == null || root.right == prev) {
list.add(root.val);
prev = root;
root = null; //No: Out of memory
} else { //Right Node Exists
stack.push(root);
root = root.right;
}
}
return list;
}4, Sequence traversal:
Iteration: [Use Queue] (Use Queue Reason: Layer by layer from left to right [Parent node A precedes parent node B, and children of parent node A precede children of parent node B]):
First enter the queue at the root, then begin to take out the current node continuously to determine if the current node has left node, enlisted node, right node and enlisted node.
// Sequence Traversal [Iteration]
public void levelOrderTraversal() {
if (root == null)
return;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
// As long as the queue is not empty: keep queuing and join the left and right child nodes of the queue
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
System.out.println(node.elmement);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}5, Allow external traversal of binary tree elements (design interface)+ Enhanced Traverse and Post-order traversal (prefix, mid-order is the same as post-order)
(1) Sequence traversal:
1. Hierarchical traversal [interface design in case of elements that allow external traversal of a binary tree]

--------------------------------------------------------------------------------------------------------------------------------
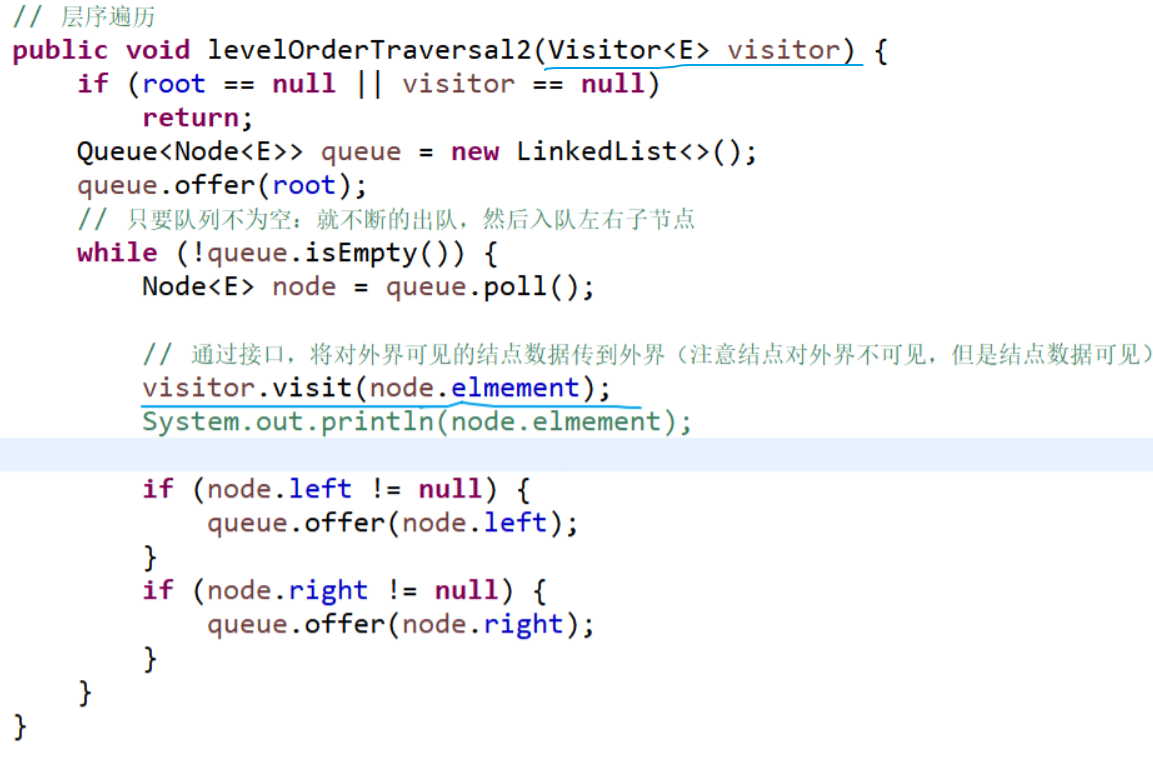
-------------------------------------------------------------------------------------------------------------------------------
(2) Hierarchical traversal [interface design for situations where elements of a binary tree are allowed to be traversed outside]+Enhanced traversal:
Enhanced traversal: Controls the stop of traversal by the return value of an interface method (so interface methods need to be written as controllable, such as Boolean types)

-------------------------------------------------------------------------------------------------------------------------------
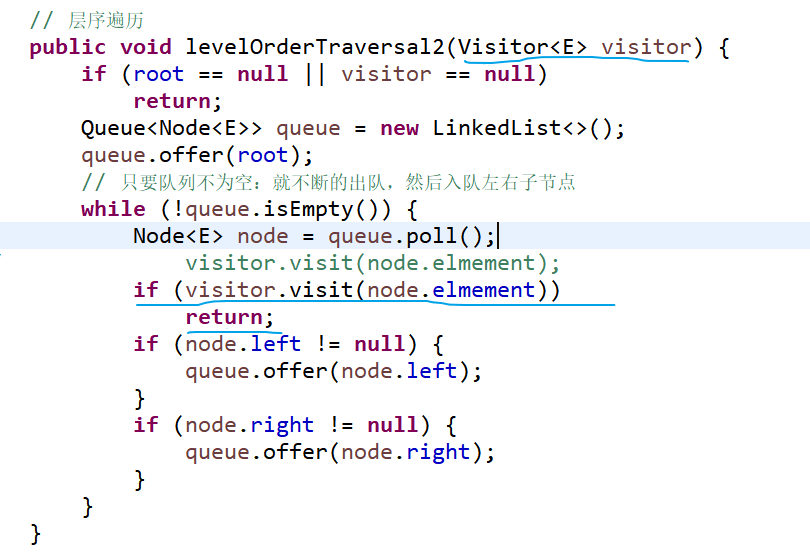
--------------------------------------------------------------------------------------------------------------------------------
(2) Post-order traversal:
(1) Post-order traversal (interface design for allowing external traversal of binary tree elements) is consistent with the order (omitted)
(2) Post-order traversal [interface design to allow external traversal of binary tree elements] + enhanced traversal:
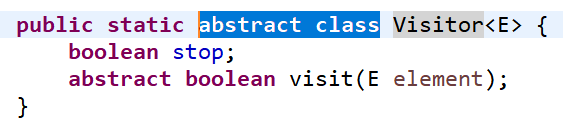
-------------------------------------------------------------------------------------------------------------------------------
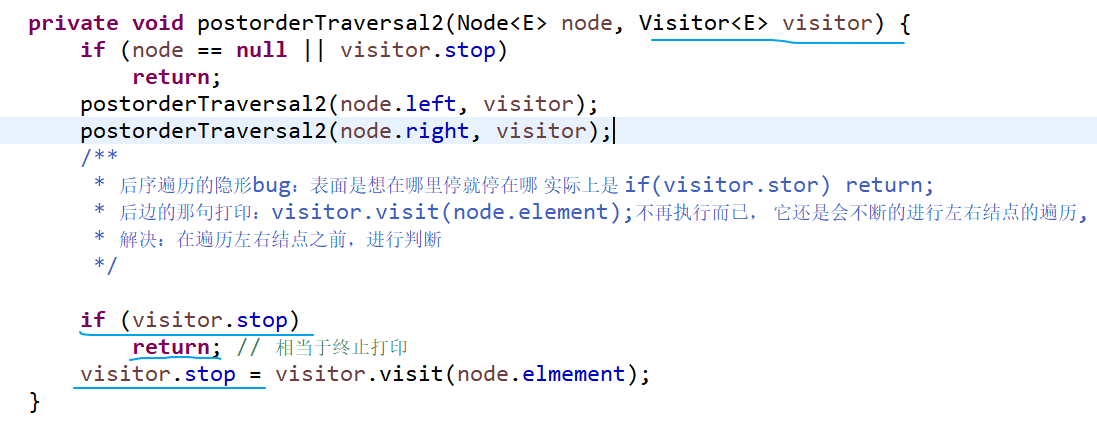
---------------------------------------------------------------------------------------------------------------------------------
6. Front and rear nodes:
^ The premise is that only middle-order traversal can have so-called precursor and backward nodes.
(1) Precursor node: the previous node when traversing in middle order.
That is, the preceding node (that is, the previous node smaller than the current node).
<. Where does a node have a chance to have a precursor (root and right):
<. Previous Node: Need to be nearest.
1. Root (look left, find the largest left interval, close to)
(See root, find root)
Method (interface):
public Node<E> predecessor(Node<E> node){
//Current incoming node (Yes, you need to decide if there is a left (left, no right)
node = node.left;
//1 If the node is not empty: as the root, go to the left interval to find the largest
// (2) If the node is empty: find the root ("parent node") and determine if it constitutes a "root-right" relationship. [The process of finding is counter-thinking: because you need to traverse while("root-left"), jumping out of the loop is finding the "root-right" relationship.)
}
Specific code:
// Precursor Node
public Node<E> predecessor(Node<E> node) {
// There is a left node (left.right.right.right...)
Node<E> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
// No left node (the view finds the right node of the first parent equal to the current node)
// If it has always been left of the parent node, continue to the parent node of the previous level
while (node.parent != null && node.parent.left == node) {
node = node.parent;
}
// Come here: Either the parent node is null or the current node is the right node of the parent node
return node.parent;
}(2) Back-drive nodes: the same analysis
7. Tree depth:
^ Hierarchical traversal + an auxiliary variable to determine that the node of the current layer has traversed to the last node
8. Is it a complete binary tree?
Node situation analysis of a complete binary tree:
(1) Traverse through the current node: left node, right node--correct
(2) with left node and no right node -- normal
(3) No left node, right node -- Abnormal
(4) No left node, no right node -- normal
Analysis: Once the first node has no right node, the next nodes are all leaf nodes! [and this process, once it occurs, is false if there is a right node and no left node's "out of bounds" behavior]
Code for complete binary tree:
// Determine whether it is a complete binary tree (Method 2: Build on the basis of sequence traversal as long as it is a binary tree, plus special cases)
public boolean isComplete2() {
if (root == null)
return false;
Queue<Node<E>> queue = new LinkedList<>();// A mistake was made: Queue is an interface, not a direct new
// Leaf State
boolean leaf = false;
queue.offer(root);
while (!queue.isEmpty()) {
// Out, back into the left and right subtree nodes
Node<E> node = queue.poll();
if (leaf && node.isLeaf()) {
return false;
}
if (node.left != null) {
queue.offer(node.left);
} else if (node.right != null) { // Otherwise left is empty, right is not empty
return false;
}
if (node.right != null) {
queue.offer(node.right);
} else { // Otherwise the right side is empty, the left side may be empty, or it may not be empty [the first empty right node was found, and the next nodes are all leaf nodes]
// Then start the state of the leaf nodes
leaf = true;
}
}
return true;
}
 https://www.cnblogs.com/shan333/p/15492654.html
https://www.cnblogs.com/shan333/p/15492654.html