1, Introduction to two-dimensional rectangular layout

   the two-dimensional rectangular layout problem can be simply understood as: given a rectangular material, multiple small rectangles with different sizes need to be cut from it. How to cut them to maximize the utilization of materials.

2, Method introduction

  the editor feels that the key steps to solve this problem are as follows:

1. How to generate a placeable position for a small rectangle

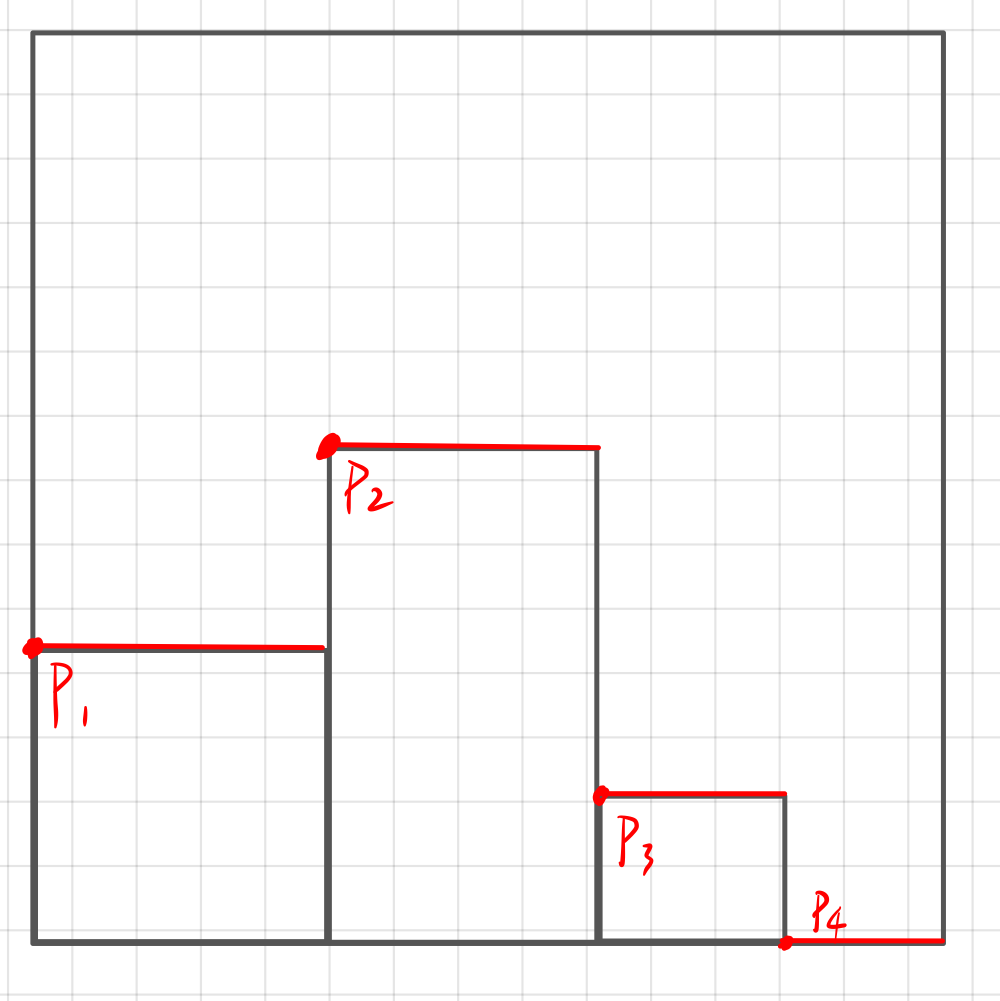
  Xiaobian generates new positions by updating the red line at the top of the small rectangle in real time, that is, p1, p2, p3 and p4 in the figure below. Xiaobian stores these red lines through a linked list, that is, the x,y coordinates of p and the length of the line.

   when the lower left corner of a rectangle is placed in p4, if the width of R4 is equal to the length of l4 or very close to the length of l4 (it can be judged by the minimum edge of the existing small rectangle. If the length of l4 minus the width of R4 is less than the minimum edge, there is no need to generate line l5), I directly move l4 up to the top of R4; Otherwise, the length of l4 is equal to the width of R4 and a new line l5 is generated. (note that the width of the small rectangle here refers to the length of the side parallel to the x axis)

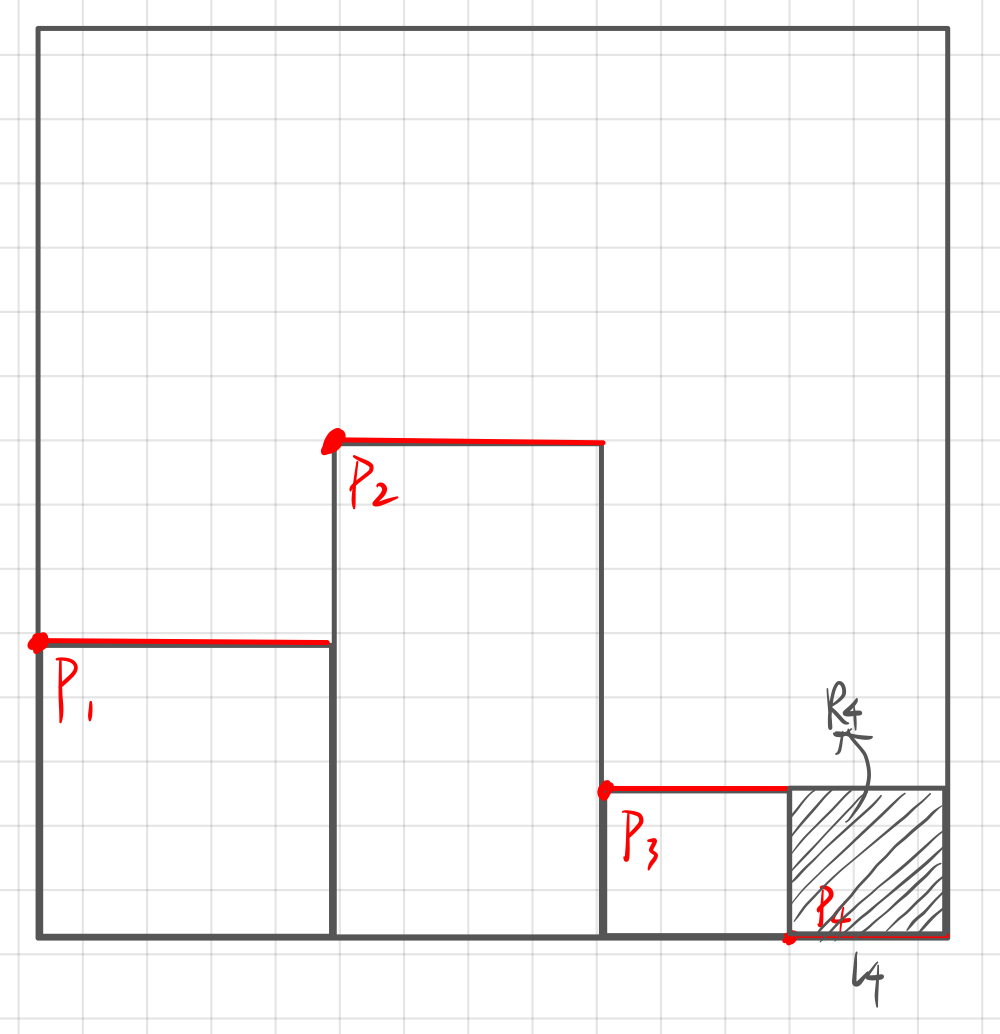
   when the selected position cannot be placed in any rectangle, I directly move the line at this position to the position with the same height as the shorter one of the two adjacent lines. If there is only one adjacent line, I can directly move to the height of the high line. (Note: after moving, the two lines will be merged to generate a longer line, that is, a wider position.)
  as for how to select the first rectangle, Xiaobian is to select the first small rectangle of the sequence, so that the solution will change with the change of the sequence. The generation of the first red line is also simple, that is, the bottom edge of the large rectangle.

2. How to select a placeable location from placeable locations to perform the current small rectangular layout

  because Xiaobian was lazy, he chose the simplest way, that is, the position with the smallest y.

3. How to select a small rectangle that best fits the placeable position selected in 2

   here, Xiaobian also chose the simplest way, that is, the scoring method. Put each small rectangle in this position, and then give it a score. The scoring method of the minor editor is:

(int) (width of small rectangle / length of position) * 100 / 10  

  for the rectangle with the same highest score, the small series selects the first rectangle with the highest score in the sequence. The above scoring method is actually selected to make the later heuristic algorithm play a greater role. Otherwise, in the face of the same position, the small rectangle with the width closest to the length of the position will be preferentially selected, so the mutation ability of the solution will become worse. Using the small series method, that is, whether it is 0.96 or 0.91, the final score is 9 points. In this way, the solution will change accordingly with the change of the sequence. Of course, this scoring method is only the simplest way, and there are many methods to choose from. For example, the higher the matching degree between a rectangle and space, the higher the score. In this way, not only width but also height are considered. The solution layers obtained by this scoring method will be relatively flat. Other methods will not be discussed in Xiaobian. Everyone is free to imagine. (Note: the small rectangle can be rotated. It's better to rotate it and give a score when scoring, so that the solution can be better.)

4. How to update solution

   the method of updating the solution is also very simple. Just update the sequence of small rectangles. When it comes to updating the sequence, the heuristic algorithm is more suitable. Xiaobian uses tabu search. Of course, other heuristics can drop. You can use several methods and compare them yourself.

Example 1 layout process

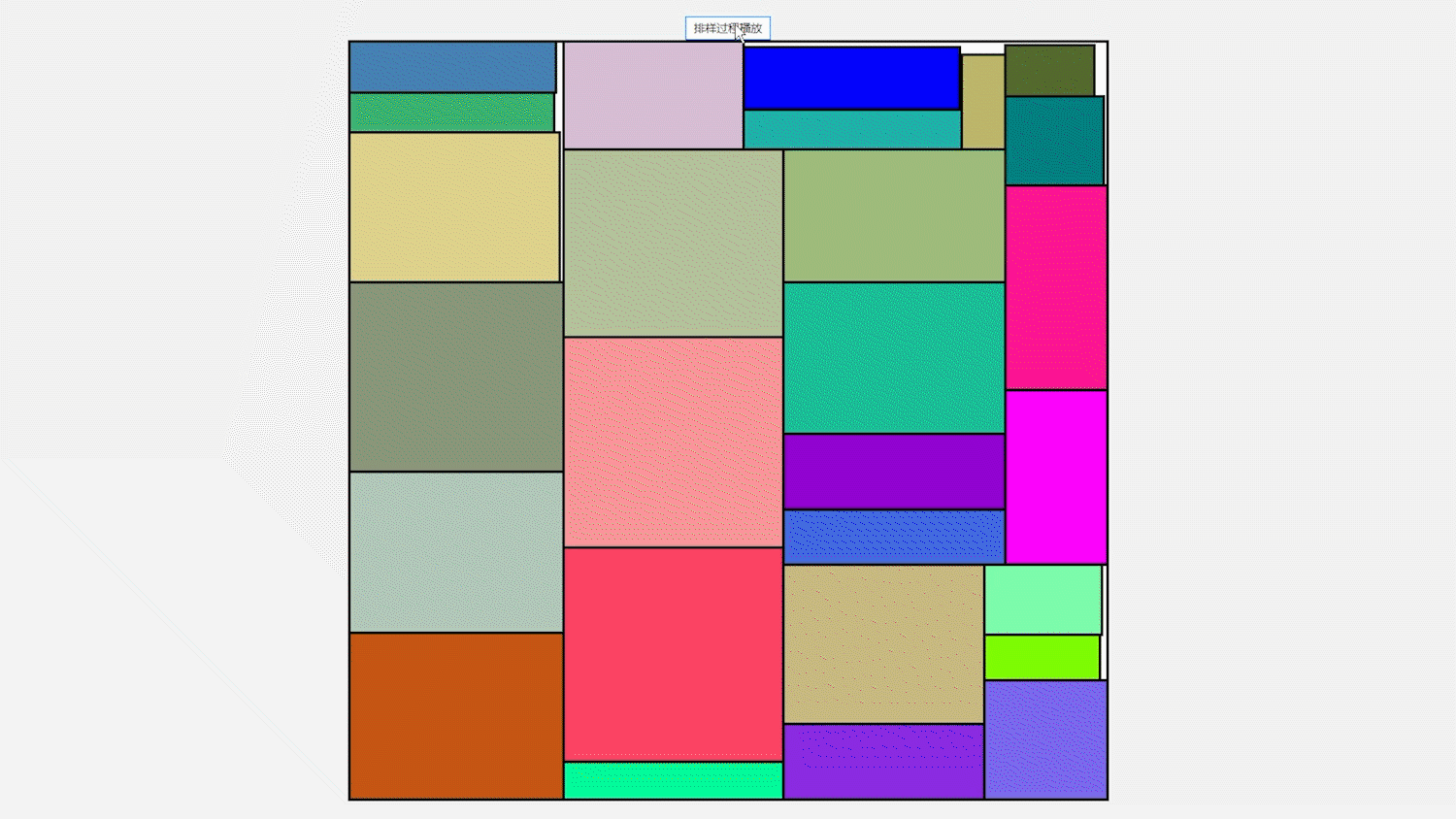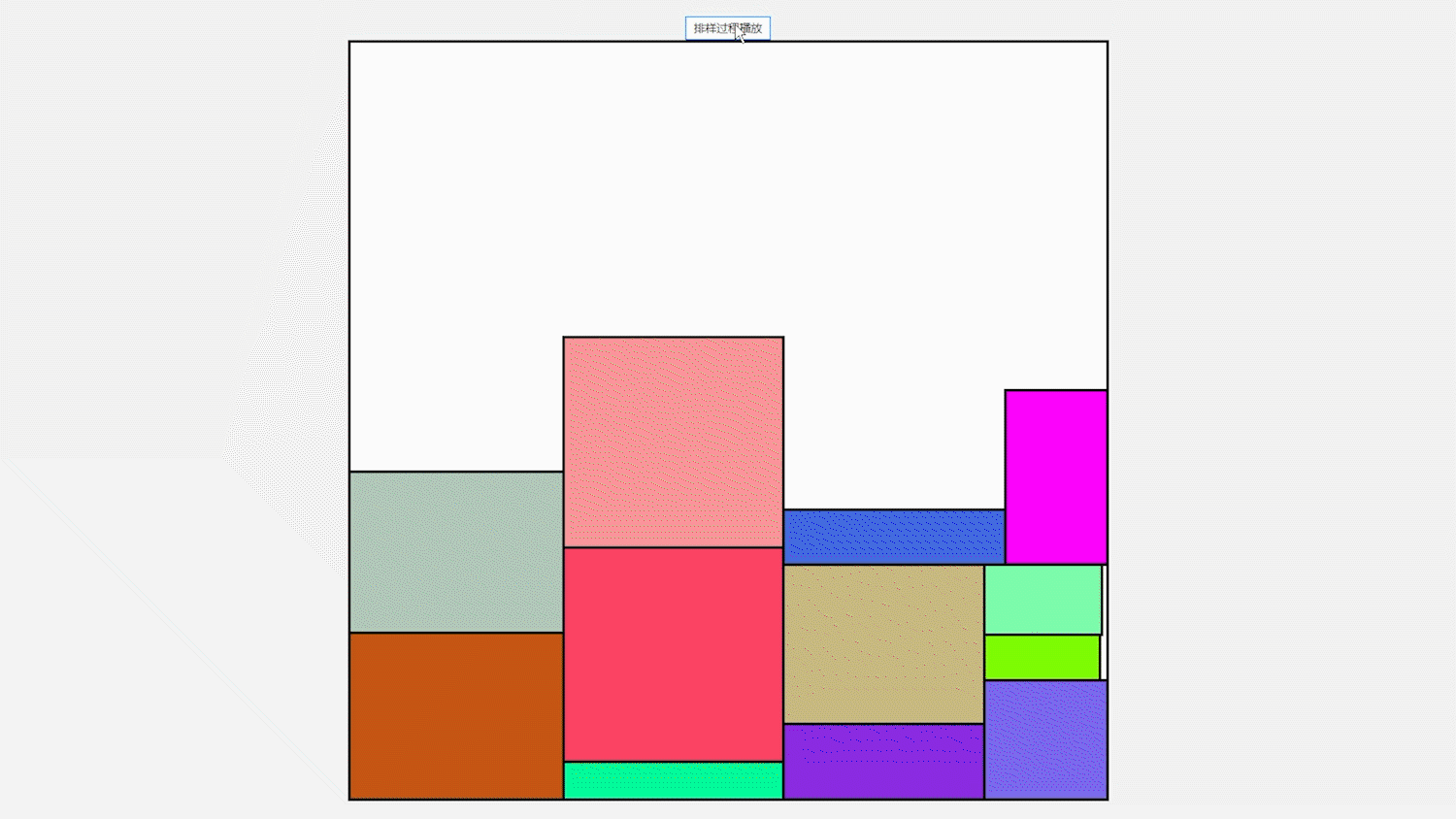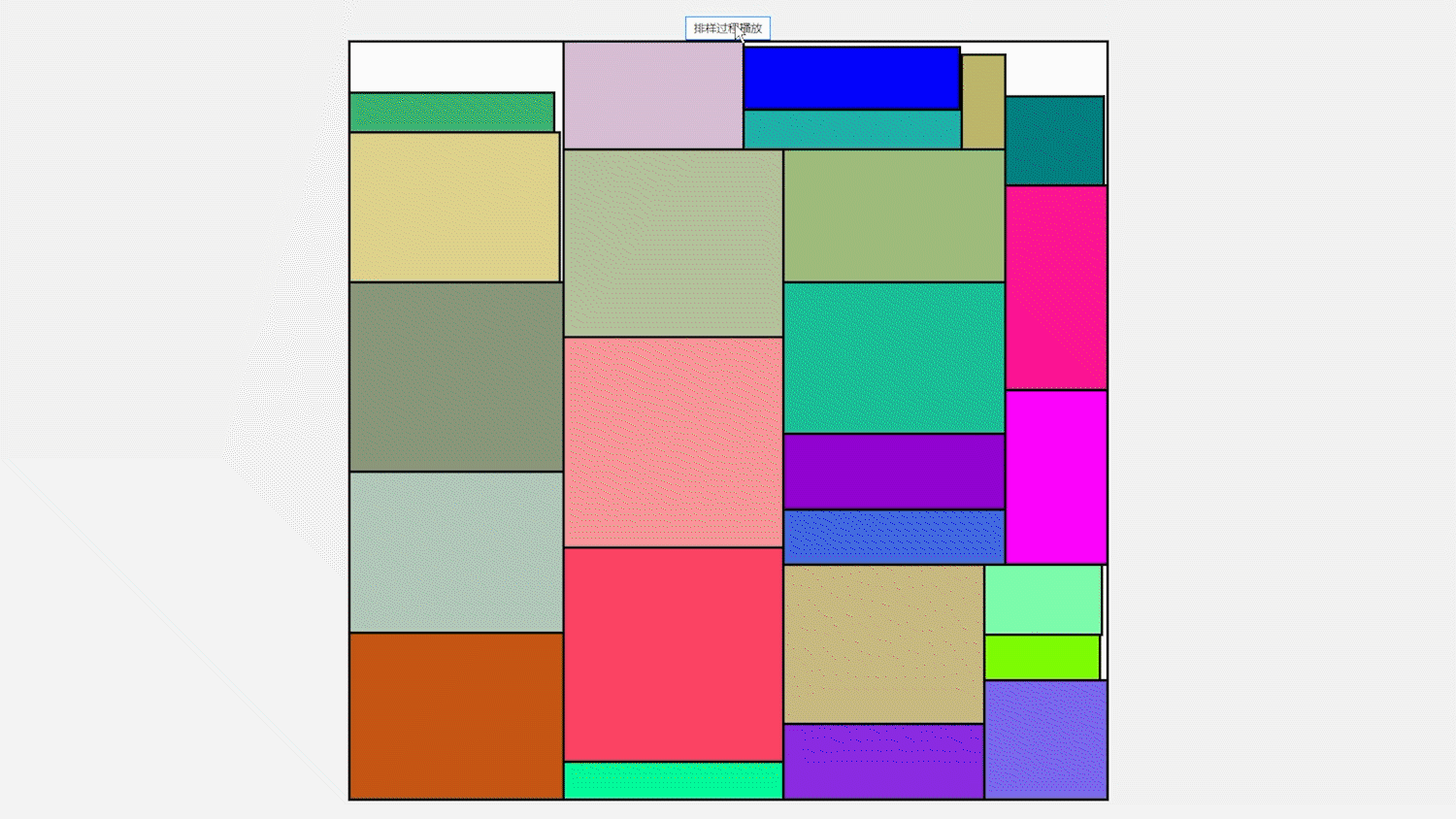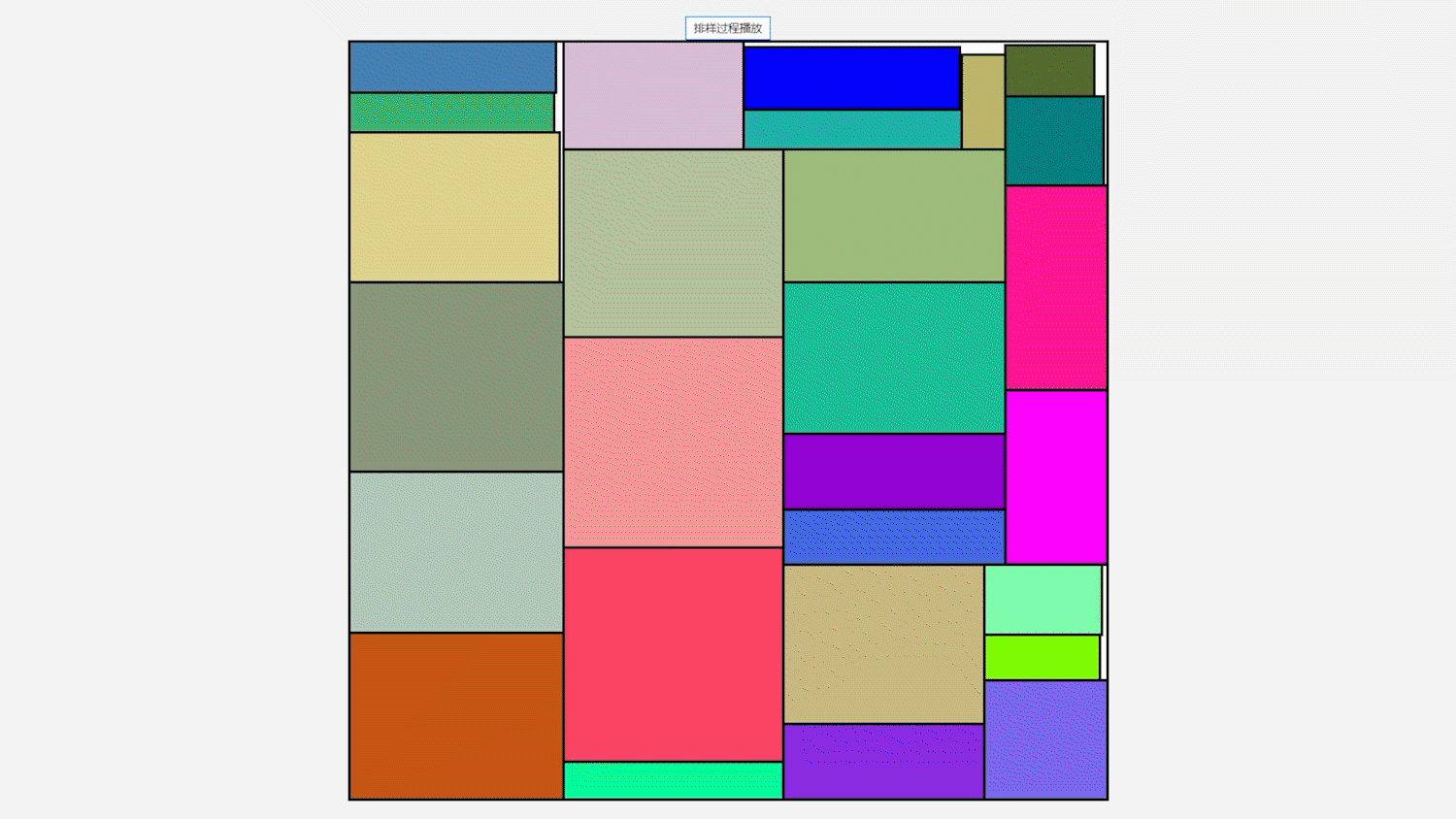
3, Algorithm test

   the data used in the test and the layout effect are shown below. This effect shows that JavaFx technology is used. This technology is most suitable for the verification of the algorithm. Whether the solution is correct can be known by drawing a diagram.

Example 2 layout process

Example 1 data:
400 400(Large rectangle)
59 115
26 99
68 97
41 63
99 116
21 60
79 118
113 85
86 55
33 114
76 70
27 47
117 40
30 46
60 62
87 55
21 108
60 67
82 93
44 49
84 96
89 34
47 34
94 44
117 80
91 62
112 73
37 92
50 48
113 100
24 55
56 27
103 21
61 24
116 111
51 62
67 76
95 57
113 116
63 49
44 56
52 47
33 66
102 53
117 107
40 106
109 27
79 99
40 82
98 96
105 105
94 31
97 78
50 23
86 22
39 59
54 92
37 67
81 102
58 33
113 88
117 71
20 58
65 63
20 116
114 69
117 29
99 88
90 49
35 80
84 87
79 111
97 25
115 21
82 66
79 84
71 38
68 80
57 82
30 73
102 31
68 42
109 106
40 42
24 71
95 101
39 94
100 108
102 26
57 89
108 54
92 107
38 62
38 32
115 46
68 37
106 84
55 73
48 103
107 64

Example 2 data:
   DamRectangle bigRectangle = new DamRectangle(1, 500, 900, 1);
   List<DamRectangle> smallBigRectangleList = new ArrayList<>();
   smallBigRectangleList.add(new DamRectangle(0, 127, 124, 2));
   smallBigRectangleList.add(new DamRectangle(1, 131, 234, 1));
   smallBigRectangleList.add(new DamRectangle(2, 142, 127, 10));
   smallBigRectangleList.add(new DamRectangle(3, 23, 29, 4));
   smallBigRectangleList.add(new DamRectangle(4, 43, 27, 2));
   smallBigRectangleList.add(new DamRectangle(5, 48, 128, 7));
   smallBigRectangleList.add(new DamRectangle(6, 37, 63, 8));
   smallBigRectangleList.add(new DamRectangle(7, 45, 40, 6));
   smallBigRectangleList.add(new DamRectangle(8, 43, 27, 17));
   smallBigRectangleList.add(new DamRectangle(9, 48, 78, 7));
   smallBigRectangleList.add(new DamRectangle(10, 37, 35, 4));
   smallBigRectangleList.add(new DamRectangle(11, 37, 40, 6));
   smallBigRectangleList.add(new DamRectangle(12, 43, 43, 7));
   smallBigRectangleList.add(new DamRectangle(13, 48, 27, 16));
   smallBigRectangleList.add(new DamRectangle(14, 37, 123, 8));
   smallBigRectangleList.add(new DamRectangle(15, 42, 40, 10));