
preface
Data structure and algorithm is to estimate the time cost and space cost when the program runs on a large number of data sets!
1, Data structure
summary
data structure refers to the collection of data elements with one or more specific relationships.
structure
selecting an appropriate data structure can improve the operation efficiency (time complexity) and storage efficiency (space complexity) of computer programs.
- Data_Structure, which is a structure for storing data, stores some data in this structure, and there is a certain relationship between these data.
- The relationship between data elements includes three components: the logical structure of data, the physical structure of data and the operation structure of data.
- The design process of a data structure is divided into abstraction layer, storage layer and implementation layer.
- Logical structure - Abstract Layer: it mainly describes the logical relationship between data elements
- Physical structure - storage layer: mainly describes the location relationship between data elements
- Operation structure - implementation layer: mainly describes how to implement data structure
There are two types of data structures: linear data structures and nonlinear data structures
Linear data structure
One dimensional array, linked list, stack, queue, string
- Array: it consists of elements of the same type and is stored in a continuous block of memory. Random access is supported, and only one subscript is required to access the element. Therefore, when inserting, it can be inserted into a specific position according to the subscript, but at this time, the elements behind it have to move one bit to the back. Therefore, the insertion efficiency is relatively low, the update and deletion efficiency is also relatively low, and the query efficiency is very high. The query efficiency time complexity is 1. Utils commonly used in Java include: String [], int [], ArrayList, Vector, CopyOnWriteArrayList, etc.
- Linked list: although it is a linear list, it does not store data in a linear order. It does not use continuous memory space to store data. The insertion efficiency is relatively high. When inserting, you only need to change the connection between the front and back nodes. The query efficiency is relatively low. If the implementation is not good, the whole link needs to be found to find the elements that should be found.
- Stack: it is a special linear table. It can only be operated at one end of the linear table. Operation is allowed at the top of the stack and not at the bottom of the stack. The characteristics of the stack are: first in first out, or last in first out. The operation of putting elements from the top of the stack is called push, and taking out elements is called pop.
- Queue: a linear first in first out table. The queue realized by array is called sequential queue, and the queue realized by linked list is called chain queue. Random access is not supported. You can only add elements from the end of the team (join the team), and you can only take elements from the head of the team (leave the team). Queues also include single order queues, two-way queues, blocking queues, etc.
- String: also known as string, it is a priority sequence composed of N characters. In Java, it refers to string, which is stored by char [].
KMP algorithm: Knuth Morris Pratt string search algorithm, referred to as "KMP algorithm" for short, is a classical algorithm to solve whether the pattern string has appeared in the text string, and if so, the earliest position.
The core idea of KMP algorithm is to make full use of the calculation results of the last mismatch and avoid the calculation work of "everything starts again".
The key point is: during string comparison, the comparison position of the main string does not need to go back.
Nonlinear data structure
2D array, multidimensional array, tree, hash table, graph
- Two dimensional array and multi-dimensional array: nothing more than String [] [], int [] [], etc
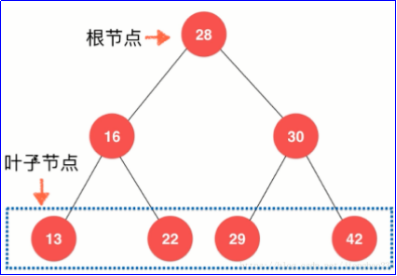
- Tree: it is a set with hierarchical relationship composed of n (n > = 1) finite nodes. Non sorting tree is mainly used for data storage and display. The sorting tree is mainly used for algorithms and operations. The TreeNode in HashMap uses the red black tree algorithm. B + tree has a typical application in the indexing principle of database.
Three traversal methods of tree
- First order traversal: root node → left subtree → right subtree
- Middle order traversal: left subtree → root node → right subtree
- Post order traversal: left subtree → right subtree → root node
Free tree / ordinary tree, binary tree, complete binary tree, full binary tree, binary search tree, red black tree, B tree, B + tree
- Free tree / normal tree: there are no constraints on child nodes.
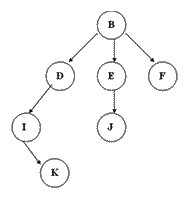
- Binary tree: a tree with at most two child nodes per node is called a binary tree.
- General binary tree: the parent node of each child node does not necessarily have two child nodes. The binary tree becomes a general binary tree.
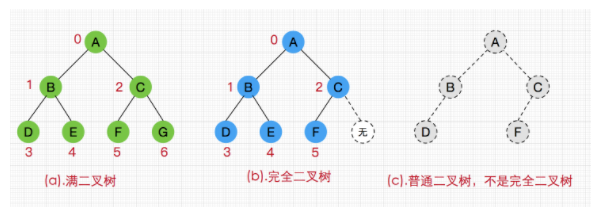
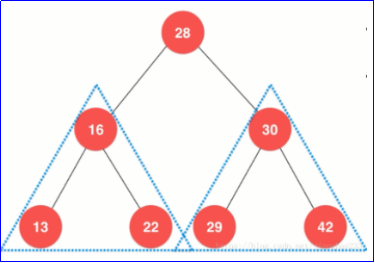
- Complete binary tree: except that the node of the last layer of the tree does not need to be full, each other layer is full from left to right. If the node of the last layer is not full, it is required that the left is full and the right is dissatisfied. heap is a complete binary tree, usually implemented as an array.
- Full binary tree: except leaf nodes, each node has two children
- Binary search tree: binary search tree, also known as binary sort tree and binary search tree. It's orderly. If it is not empty, the value of the left subtree node is less than the value of the root node; The value of the right subtree node is greater than that of the root node.
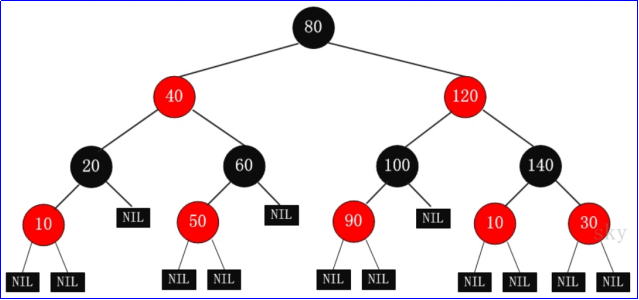
- Red black tree: the binary tree is balanced by formulating some red black marks and left-right rotation rules.
- The root node is black.
- Each node is either black or red.
- Each leaf node (NIL) is black. [Note: the leaf node here refers to the leaf node that is empty (nil or null!]
- If a node is red, its child nodes must be black.
- All paths from a node to its descendants contain the same number of black nodes.
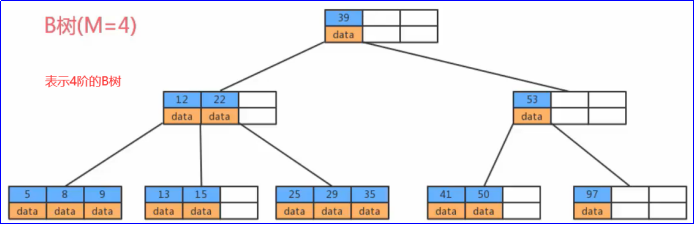
- B tree/B-tree: also known as B tree and B-tree. It is also called balance multi-channel lookup tree.
- Each node has at most M-1 key s and is arranged in ascending order (for example, 5, 8, 9 in the figure, at most 3)
- Each node can have up to M child nodes (up to 4 child nodes under 5, 8 and 9)
- The root node has at least 2 child nodes (such as the left and right of the second floor in the figure)
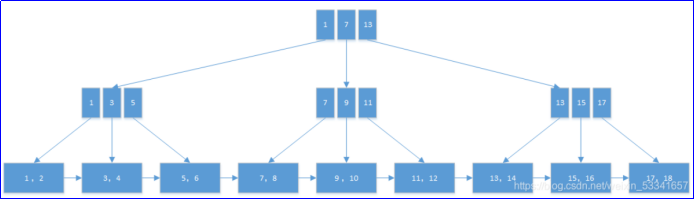
- B+tree: also known as B +. It is a variant of B-tree and a multi-path search tree.
- The leaf nodes of B + tree will be connected into a linked list. The leaves themselves are sorted from small to large according to the size of the index value. That is, the linked list is from small to large. There are more linked lists to facilitate searching data in the range.
- There are two kinds of nodes in B + tree, one is index node and the other is leaf node.
- The index node of B + tree does not save records, but is only used for indexing. Save only key, not value.
- The number of subtree pointers of non leaf nodes is the same as that of keywords.
-
Hash table: hash is called hash or hash, which is to transform an input of any length (also known as pre mapping) into a fixed length output, which is the hash value. It is generally realized by hash algorithm. The so-called hash algorithms are hash algorithms, which transform the input of any length into the output of fixed length, and the output is the hash value (such as MD5,SHA1, encryption and decryption algorithm, etc.). In short, it is a function that compresses a message of any length to a message digest of a fixed length.
- hashCode: all class es will have the default hashCode method in Object.java. If they do not rewrite it, the default is that the native method calculates an int number through the object's memory + object value, and then through the hash hash algorithm. For different objects and different values, the calculated hashCode may be the same.
- Hash table: the data storage method is a data structure integrating array and linked list. Such as HashTable and HashMap. Hash table has fast (constant level) query speed and relatively fast addition and deletion speed, so it is very suitable for use in the environment of massive data. Generally, the method of realizing hash table adopts "zipper method", which can be understood as "array of linked list".
-
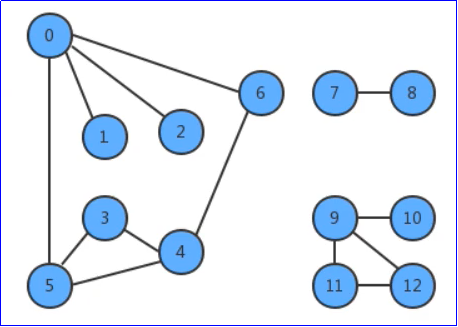
Graph: the data elements of a graphical structure are many to many relationships.
- Undirected graph
- Directed graph
aggregate
A whole composed of one or more definite elements is called a set. In Java, it can be understood in a broad sense that the classes that implement the Collection interface are called collections.
Comparison and selection of data structures
compare
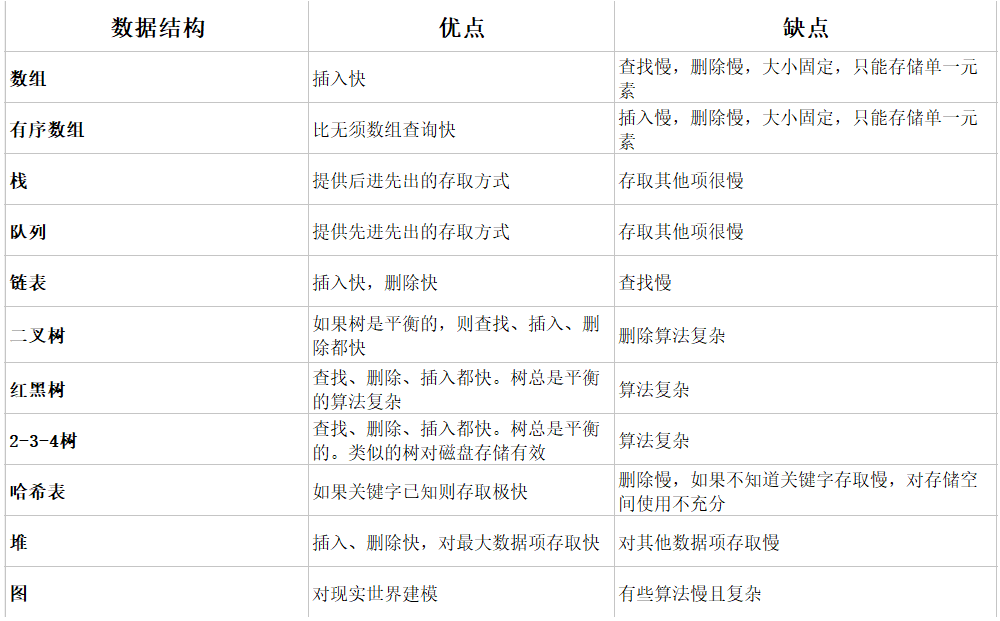
Common data structures
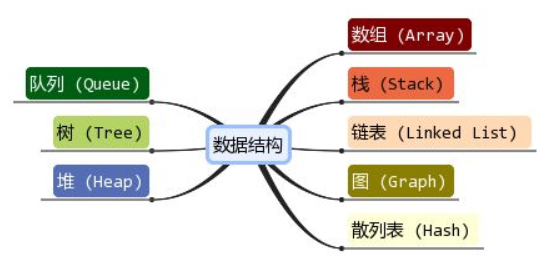
Data structure selection
2, Algorithm
summary
- Space complexity: in a word, this algorithm consumes additional storage space when the scale is n.
- Time complexity: in a word, when the scale of this algorithm is n, the number of statements executed in an algorithm is called statement frequency or time frequency.
- Stability: it mainly describes the algorithm. After each execution, the results are the same, but they can be input in different order, which may consume different time complexity and space complexity.
Five features of the algorithm
Finiteness, certainty, feasibility, input and output.
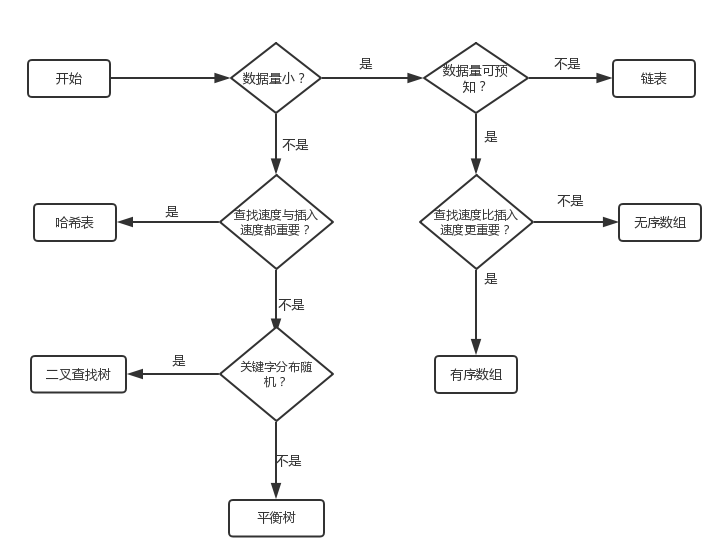
Binary search algorithm
Half search is also called "binary search", and the algorithm complexity is nlog2n. The search sequence must be ordered before half search can be carried out.
- Advantages: less comparison times, fast search speed, good average performance and less system memory.
- Disadvantages: the table to be queried is required to be an ordered table, and it is difficult to insert and delete.
Half search idea
set the ordered order table {a [0], a [1],..., a [n-1]}, first find the subscript mid of the middle element in the search interval, and then compare the position value a[mid] with the value key to be searched.
- If key=a[mid], the search succeeds and the subscript is returned;
- If key < a [mid], the element to be searched is on the left side of mid, narrow the search interval to the first half of the table, and then search in half;
- If key > a [mid], the element to be searched is on the right side of mid, narrow the search interval to the second half of the table, and then perform a half search.
Process example
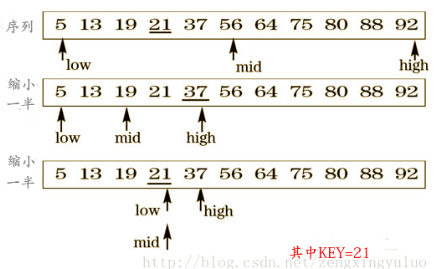
Code example, two ways (recursive and non recursive)
public class Test {
//non-recursive
public int binSearch(int a[], int low, int high, int key){
while(low<=high){
int mid=(low+high)/2;
if(a[mid]==key)
return mid;
else if(key<a[mid])
high=mid-1;
else
low=mid+1;
}
return -1;
}
//recursion
public int binRecSearch(int a[], int low, int high, int key){
if(low<=high){
int mid=(low+high)/2;
if(a[mid]==key)
return mid;
else if(key<a[mid])
return binRecSearch(a, low,mid-1, key);
else
return binRecSearch(a,mid+1, high, key);
}
else
return -1;
}
//test
public static void main(String[] args){
int[] a = { -36, -3, 5, 16, 24, 30, 78, 84, 345, 1004};
Test test = new Test();
//non-recursive
int pos1=test.binSearch(a,0,a.length-1,-3);
if(pos1!=-1)
System.out.println("-3 Where the subscript is "+pos1);
else
System.out.println("The number 84 cannot be found!");
//recursion
int pos2=test.binRecSearch(a,0,a.length-1,84);
if(pos2!=-1)
System.out.println("84 Where the subscript is "+pos2);
else
System.out.println("The number 84 cannot be found!");
}
}
Implementation of sorting algorithm
1. Bubble sorting
basic thought
Bubble Sort repeatedly visits the sequence to be sorted, compares two elements at a time, and exchanges them if their order is wrong. The work of visiting the sequence is repeated until there is no need to exchange, that is, the sequence has been sorted.
code implementation
/**
* Bubble sort: compare adjacent elements. If the first is larger than the second, swap them.
*/
private static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length; i++) {
for (int j = i+1; j < arr.length; j++) {
if (arr[i] > arr[j]){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
}
2. Quick sort
basic thought
Quick Sort uses the divide and conquer strategy to divide a sequence (list) into two sub lists.
Steps:
- Picking out an element from a sequence is called a "pivot".
- Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition, the benchmark is in the middle of the sequence. This is called a partition operation.
- recursively sorts subsequences that are smaller than the reference value element and subsequences that are larger than the reference value element.
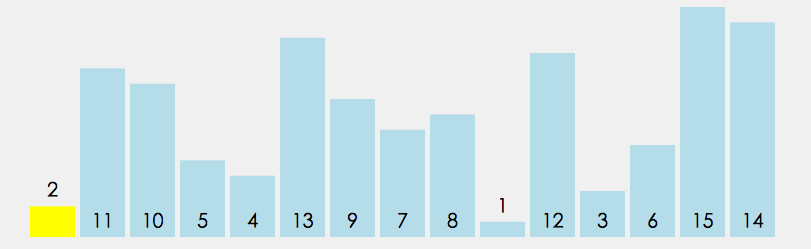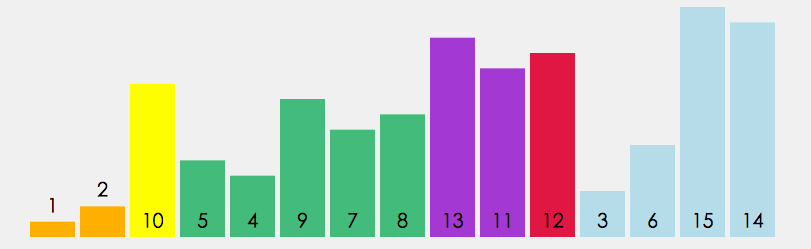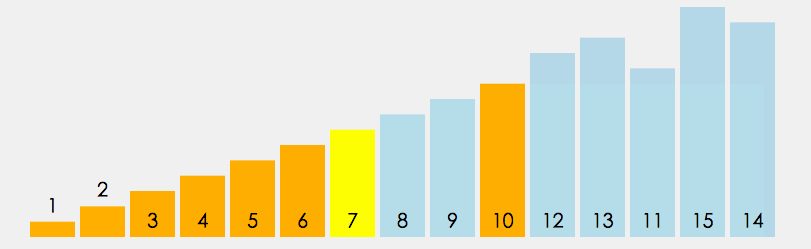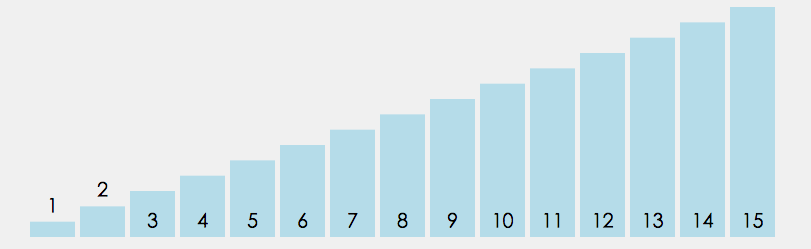
code implementation
/**
* Quick sort: select an element from the sequence, which is called "benchmark". All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark
*/
private static void quickSort(int[] arr, int start, int end){
//End left and right recursion
if (start < end){
int base = arr[start]; //Select the first number as the benchmark
int temp; //Record temporary intermediate value
int i = start, j = end; //start is leftmost and end is rightmost
do {
while ((arr[i] < base) && (i < end))
i++;
while ((arr[j] > base) && (j > start))
j--;
if (i <= j){
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}while (i <= j);
if (start < j)
quickSort(arr, start, j);
if (end > i)
quickSort(arr, i, end);
}
}
3. Select Sorting
basic thought
it is a simple and intuitive sorting method, which finds the minimum value in the sequence each time, and then puts it at the end.
code implementation
/**
* Selective sorting: it is a simple and intuitive sorting method to find the minimum value in the sequence each time, and then put it at the end.
*/
private static void selectSort(int[] arr){
int temp;
for (int i = 0; i < arr.length; i++) {
int k = i;
for (int j = arr.length-1; j > i; j--) {
if (arr[j] < arr[k]) k = j;
}
temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;
}
}
4. Insert sort
basic thought
by constructing an ordered sequence, for unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert it.
code implementation
/**
* Insert sort: by constructing an ordered sequence, for unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert.
* Starting with the first element, the element can be considered to have been sorted
* Take out the next element and scan from back to forward in the sorted element sequence
* If the element (sorted) is larger than the new element, move the element to the next position
* Repeat step 3 until you find a location where the sorted element is less than or equal to the new element
* Insert the new element into this location
* Repeat step 2
*/
private static void insertSort(int[] arr){
int temp, j;
for (int i = 1; i < arr.length; i++) {
temp = arr[i];
for (j = i; j > 0 && temp < arr[j-1]; j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
5. Merge and sort
basic thought
merge sort is a typical divide and conquer algorithm. It continuously divides an array into two parts, sorts the left sub array and the right sub array respectively, and then combines the two arrays into a new ordered array.
code implementation
/**
* Merge sort: it is an effective sort algorithm based on merge operation. Merge refers to the operation of merging two sorted sequences into one sequence
* Apply for space so that its size is the sum of two sorted sequences. The space is used to store the merged sequences
* Set two pointers. The initial position is the starting position of the two sorted sequences
* Compare the elements pointed to by the two pointers, select the relatively small element, put it into the merge space, and move the pointer to the next position
* Repeat step 3 until a pointer reaches the end of the sequence
* Copy all the remaining elements of another sequence directly to the end of the merged sequence
*/
private static void mergeSort(int[] arr, int left, int right){
int t = 1;// Number of elements in each group
int size = right - left + 1;
while (t < size) {
int s = t;// Number of elements in each group in this cycle
t = 2 * s;
int i = left;
while (i + (t - 1) < size) {
merge(arr, i, i + (s - 1), i + (t - 1));
i += t;
}
if (i + (s - 1) < right)
merge(arr, i, i + (s - 1), right);
}
}
//Implementation of merging algorithm
private static void merge(int[] data, int p, int q, int r) {
int[] B = new int[data.length];
int s = p;
int t = q + 1;
int k = p;
while (s <= q && t <= r) {
if (data[s] <= data[t]) {
B[k] = data[s];
s++;
} else {
B[k] = data[t];
t++;
}
k++;
}
if (s == q + 1)
B[k++] = data[t++];
else
B[k++] = data[s++];
for (int i = p; i <= r; i++)
data[i] = B[i];
}
test
package com.mizhu;
import java.util.Arrays;
public class NumberSort {
//call
public static void main(String[] args) {
int[] arr = {6, 1, 2, 7, 9, 3, 4, 5, 1, 0, 8};
System.out.println("Before sorting---");
System.out.println(Arrays.toString(arr));
// bubbleSort(arr);
// quickSort(arr,0, arr.length-1);
// selectSort(arr);
// insertSort(arr);
// mergeSort(arr,0, arr.length-1);
System.out.println("After sorting---");
System.out.println(Arrays.toString(arr));
}
}
summary
Feel useful, remember to support!!!
