Attach the program effect first:
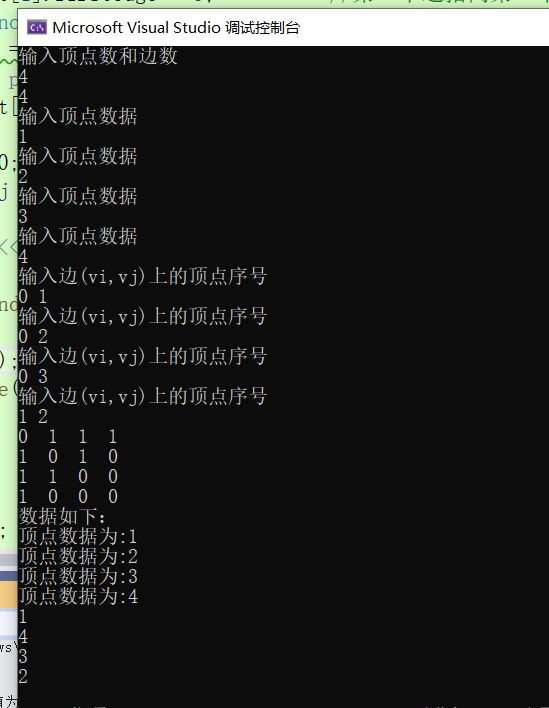
Adjacency table:
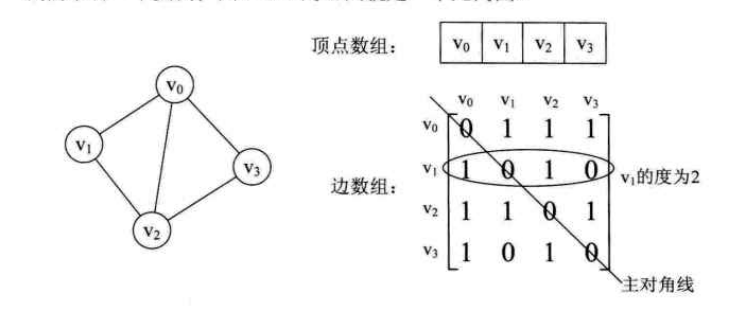
Adjacency matrix, that is, a two-dimensional array is used to store the relationship between each vertex and the corresponding edge. For example, if there are edges between two vertices, set the subscript corresponding to this two-dimensional array to a non-zero value. As shown below:
Undirected graph:
Directed graph:
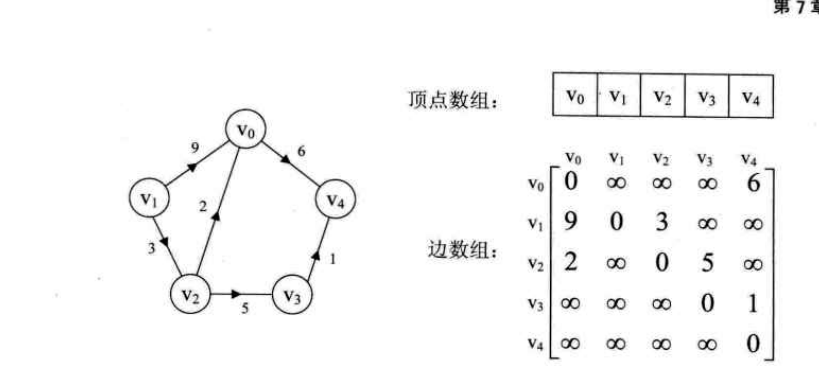
Adjacency matrix is a good graph storage structure, but it wastes storage space for graphs with fewer edges,
For example:
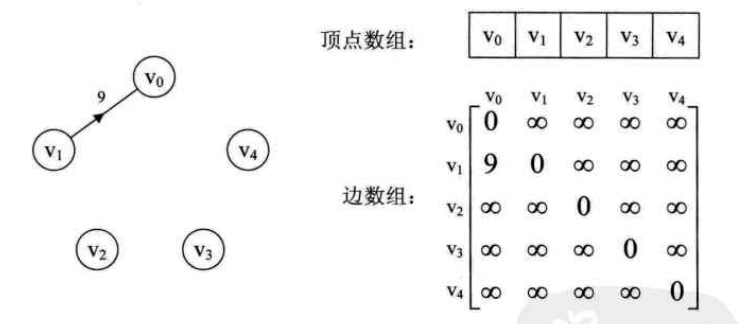
When learning linear table, we all know that sequential storage structure wastes space, so chain storage structure is introduced to save space.
Therefore, similarly, we can use chain storage structure for arcs or edges to avoid the problem of space waste.
So we introduce a new graph storage structure, adjacency table.
We store a graph by combining array with linked list, and the storage method of this combination of linked list and array is called adjacency list.
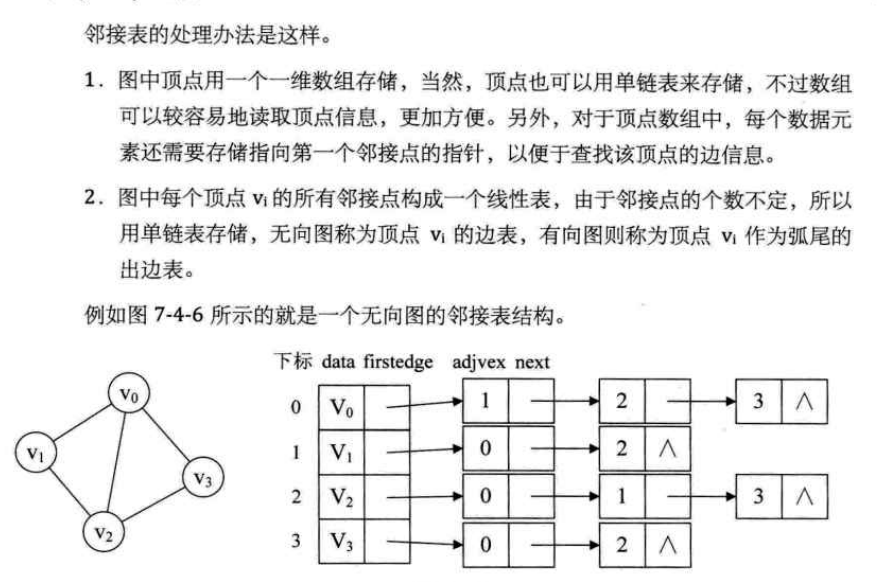

Then we probably know what the adjacency table looks like, so it's easy to implement.
Next is the definition of structure:
typedef struct Adjvex //Adjacency domain
{
int adjvex; //The adjacency point of the vertex is in the subscript of the array
int weight; //Whether you have weights depends on whether you use a directed or undirected graph
Adjvex* next; //The next adjacency point is in the subscript of the array
}*Edgenode,Adjvex;
typedef struct Vertxnode //Vertex node vertex array stores the subscript pointers of nodes and adjacent vertices
{
ElemType data;
Adjvex* firstedge;
}Vertexnode,Adjlist[MAXSIZE];
typedef struct Graphlist //Adjacency tables combine vertex arrays with the number of vertices and edges
{
Adjlist adjlist; //Vertex arrays and adjacent fields
int vexnum, edgenum; //Number of vertices and edges;
}Graphlist,*p_Graphlist;
int Visited[MAXSIZE] = {0}; //Used to indicate whether the current vertex is accessed. 1 indicates access. 0 indicates no access
int AdjRectangle[MAXSIZE][MAXSIZE]; //Two dimensional array analog adjacency matrix
For the construction of an undirected graph, we follow the principle of symmetry. This is because the two vertices pointed by an edge of an undirected graph point to each other, so each other's subscripts need to be stored in each other's adjacent vertex domain.
void CreateGraphlist(p_Graphlist p)
{
int i, j, k;
Edgenode e;
cout << "Enter the number of vertices and edges" << endl;
cin >> p->vexnum >> p->edgenum; //Enter the number of sides and tables
for (i = 0; i < p->vexnum; i++) //Initialize vertex table
{
cout << "Enter vertex data" << endl;
cin >> p->adjlist[i].data; //Vertex data assignment
p->adjlist[i].firstedge = NULL; //The provisional adjacent edge table is empty
}
for (i = 0; i < p->vexnum; i++)//Two dimensional array analog adjacency matrix | 0 0 1|
{ //for example | 0 0 1|
for (k = 0; k < p->vexnum; k++) // |1 1 0|
{
AdjRectangle[i][k] = 0; //Tentative initialization to all 0
}
}
for (k = 0; k < p->edgenum; k++)//This for loop is used to input edgenum edges
{
cout << "Input edge(vi,vj)Vertex sequence number on" << endl; //vi is the edge tail and vj is the edge head
cin >> i >> j; //If you enter 0 and 1, it means that the edge tail is v0 and the edge head tail is v1
AdjRectangle[i][j] = 1; //The corresponding array position is set to 1, which means there is a table
AdjRectangle[j][i] = 1; //The matrix is symmetric and the corresponding position is set to 1
e = (Edgenode)malloc(sizeof(Adjvex)); //Create adjacency vertex table pointer
e->adjvex = j; //The vertex of the adjacency table points to j
//e->next = p->adjlist[i].firstedge;
p->adjlist[i].firstedge = e; //The first edge points to the first edge table
e = (Edgenode)malloc(sizeof(Adjvex)); //Symmetrical structure
e->adjvex = i;
//e->next = p->adjlist[j].firstedge;
p->adjlist[j].firstedge = e;
}
for (int i = 0; i < p->vexnum; i++) { //Output adjacency matrix
for (int j = 0; j < p->vexnum; j++)
{
cout << AdjRectangle[i][j] << " ";
}
cout << endl;
}
DFSTraverse(p);
}
be careful:
Here, we must focus on the situation that a node has multiple adjacent nodes.
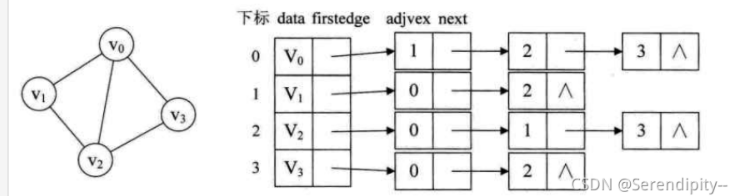
Each node in the graph has more than one adjacent node, so how does the next of these adjacent nodes point to the next adjacent node?
It's hard to imagine just looking at the program, so let's debug it.
Let's take v0 point as an example and input v1 and v3 edges (just for debug ging. Understanding one process can deduce the next process)
First establish an edge between v0 and v1
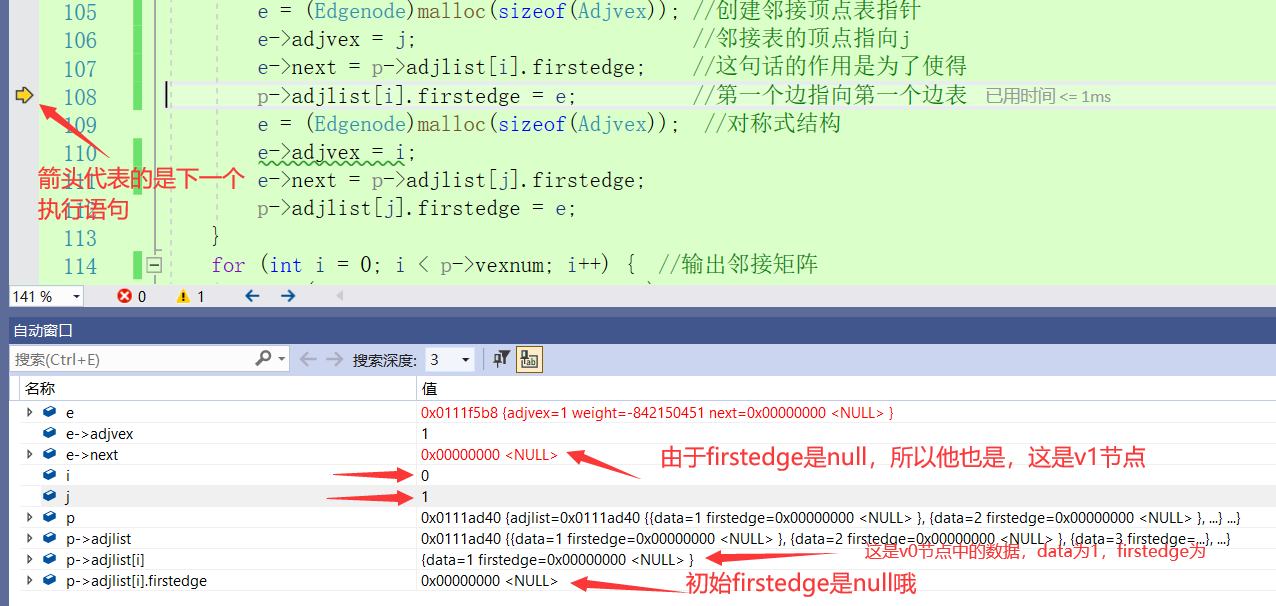
The address may be different from that in the following picture v1, but the meaning to be expressed is the same.
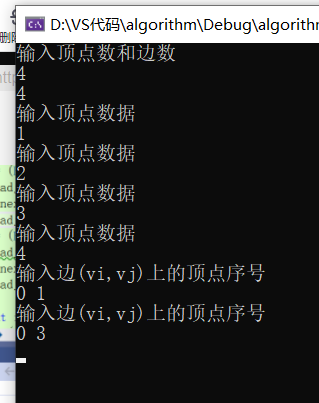
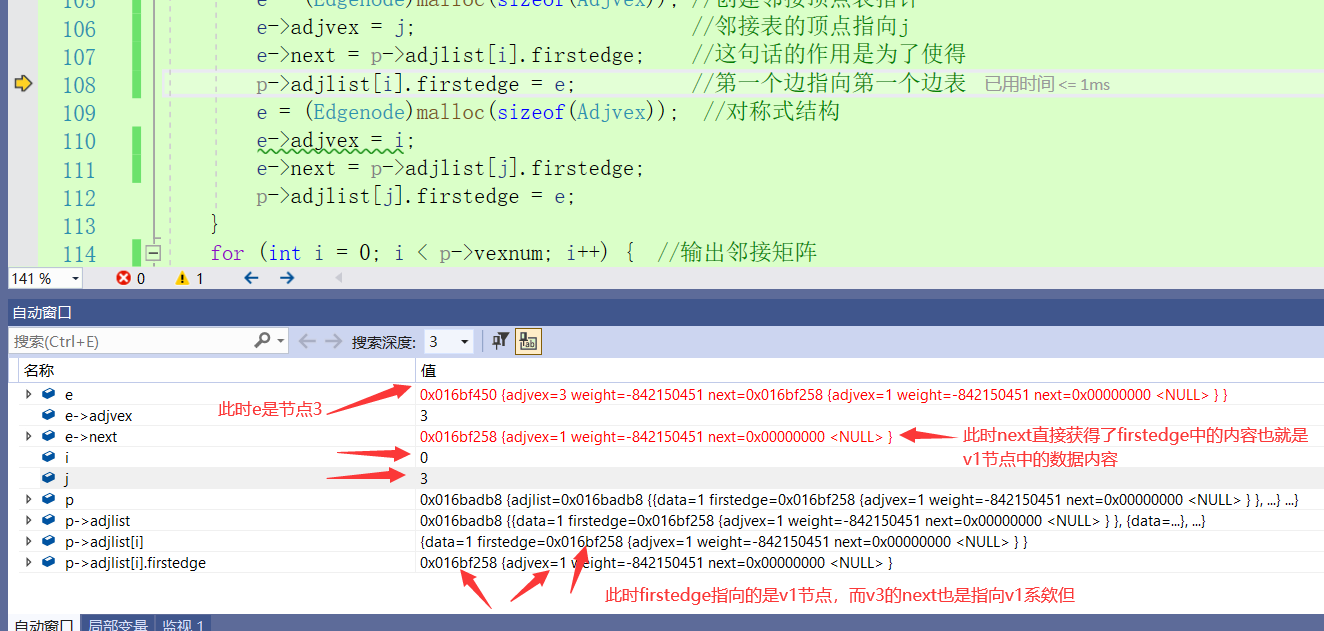
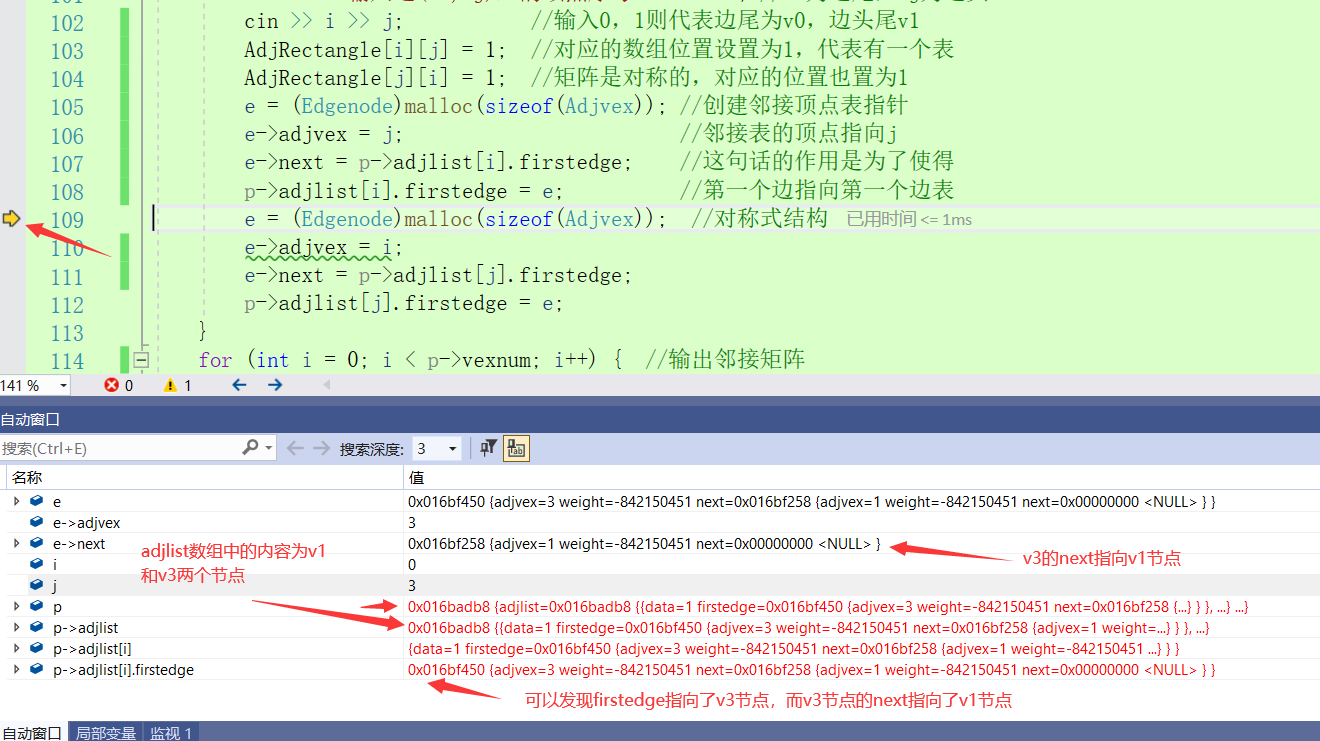
It can be found that when I input the v1 node first, the firstedge will point to the v1 node first. Since the initialization of the firstedge is NULL, the next node of v1 is NULL. After I input the v3 node, the firstedge will point to the v3 node, and the next node of v3 will point to the v1 node. This forms a loop, that is, the first input will be later.
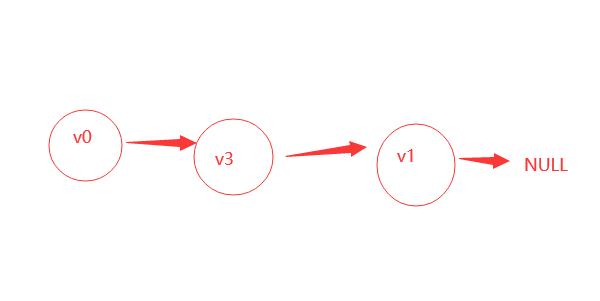
Then the creation is over. It's easier to understand the creation. If you really don't understand how to create it, you can check the dubug.
So the final play is how to traverse the whole graph.
We use the depth first traversal method
So what is depth first traversal?
Depth first traversal:
The idea is to access this vertex from a node V of the graph, and then traverse the graph depth first from the unreachable adjacency of V until all vertices connected with V with a path in the graph are accessed. In the figure above, the V0 node accesses v1 first. After v1 is accessed, v1 accesses its own adjacency point v2 first, v2 accesses its own adjacency point v3, and v3 accesses its own adjacency point v0. Later, it is found that V0 has been accessed, so it returns from v3 to v2, then returns from v2 to v1, and then returns to v0. This forms a depth first traversal. It can be found that this is achieved by recursion.
Then put the code directly at last. It is divided into recursive traversal of adjacency table and adjacency matrix.
code:
Header file code:
#pragma once #include<iostream> #include <cstdio> #include<cstdlib> typedef int Status; typedef int ElemType; typedef char cElemType; #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define MAXSIZE 20 #define make (struct student*)malloc(sizeof(struct student)); using namespace std;
Implementation code
#include<algo.h>
typedef struct Adjvex //Adjacency domain
{
int adjvex; //The adjacency point of the vertex is in the subscript of the array
int weight; //Weight
Adjvex* next; //The next adjacency point is in the subscript of the array
}*Edgenode,Adjvex;
typedef struct Vertxnode //Vertex node
{
ElemType data;
Adjvex* firstedge;
}Vertexnode,Adjlist[MAXSIZE];
typedef struct Graphlist //Adjacency table
{
Adjlist adjlist; //Vertex arrays and adjacent fields
int vexnum, edgenum; //Number of vertices and edges;
}Graphlist,*p_Graphlist;
int Visited[MAXSIZE] = {0}; //Used to indicate whether the current vertex is accessed. 1 indicates access. 0 indicates no access
int AdjRectangle[MAXSIZE][MAXSIZE]; //Two dimensional array analog adjacency matrix
void DFS(p_Graphlist p, int i)//Depth first recursive traversal of adjacency matrix
{
int j;
Visited[i] = 1; //Set to 1 if the node is accessed
cout << "Vertex data is:" << p->adjlist[i].data << endl; //Output current node data
for (j = 0; j < p->vexnum; j++)//Loop call recursion
{
if (AdjRectangle[i][j] == 1 && !Visited[j])//If the edge table is 1 and the current node has not been accessed, recursion is called
{
DFS(p, j);//j=0, 1, 2, 3, 4... Until each node is accessed recursively once
}
}
}
void DFSTraverse(p_Graphlist p)//Non recursive algorithm traverses the direct output array data
{
int i;
for (i = 0; i < p->vexnum; i++)
{
Visited[i] = 0; //Set all data to non traversal state 0 first
}
cout << "The data are as follows:" << endl;
for (i = 0; i < p->vexnum; i++)//
{
if (!Visited[i])
{
DFS(p,i);
}
}
}
//Depth first recursive algorithm for adjacency table
void AdjDFS(p_Graphlist p, int i)
{
Edgenode e;
Visited[i] = 1; //Set to 1 after accessing the current node
cout << p->adjlist[i].data << endl; //Output current data
e = p->adjlist[i].firstedge; //Assign the first adjacent contact to the edge table structure pointer
while (e)
{
if (!Visited[e->adjvex])//Determine whether the node has been accessed, and if not, perform recursive traversal
{
AdjDFS(p, e->adjvex);
}
e = e->next;//Let e point to his next position
}
}
void AdjDFSTraverse(p_Graphlist p)
{
int i;
for (i = 0; i < p->vexnum; i++)
Visited[i] = 0;//Initialize access array
for (i = 0; i < p->vexnum; i++)
{
if (!Visited[i])
{
AdjDFS(p, i);
}
}
}
void CreateGraphlist(p_Graphlist p)
{
int i, j, k;
Edgenode e;
cout << "Enter the number of vertices and edges" << endl;
cin >> p->vexnum >> p->edgenum; //Enter the number of sides and tables
for (i = 0; i < p->vexnum; i++) //Initialize vertex table
{
cout << "Enter vertex data" << endl;
cin >> p->adjlist[i].data; //Vertex data assignment
p->adjlist[i].firstedge = NULL; //The provisional adjacent edge table is empty
}
for (i = 0; i < p->vexnum; i++)//Two dimensional array analog adjacency matrix | 0 0 1|
{ //for example | 0 0 1|
for (k = 0; k < p->vexnum; k++) // |1 1 0|
{
AdjRectangle[i][k] = 0; //Tentative initialization to all 0
}
}
for (k = 0; k < p->edgenum; k++)//This for loop is used to input edgenum edges
{
cout << "Input edge(vi,vj)Vertex sequence number on" << endl; //vi is the edge tail and vj is the edge head
cin >> i >> j; //If you enter 0 and 1, it means that the edge tail is v0 and the edge head tail is v1
AdjRectangle[i][j] = 1; //The corresponding array position is set to 1, which means there is a table
AdjRectangle[j][i] = 1; //The matrix is symmetric and the corresponding position is set to 1
e = (Edgenode)malloc(sizeof(Adjvex)); //Create adjacency vertex table pointer
e->adjvex = j; //The vertex of the adjacency table points to j
e->next = p->adjlist[i].firstedge; //The purpose of this sentence is to make
p->adjlist[i].firstedge = e; //The first edge points to the first edge table
e = (Edgenode)malloc(sizeof(Adjvex)); //Symmetrical structure
e->adjvex = i;
e->next = p->adjlist[j].firstedge;
p->adjlist[j].firstedge = e;
}
for (int i = 0; i < p->vexnum; i++) { //Output adjacency matrix
for (int j = 0; j < p->vexnum; j++)
{
cout << AdjRectangle[i][j] << " ";
}
cout << endl;
}
DFSTraverse(p);
AdjDFSTraverse(p);
}
int main()
{
p_Graphlist p;
p = (p_Graphlist)malloc(sizeof(Graphlist));
CreateGraphlist(p);
}
It can be found that the traversal result of the adjacency matrix is 1 4 3 2, which is the same as the result of our debug. The node we inserted first is the end of the linked list, and then the beginning of the linked list. Therefore, the data 4 in the v3 node we inserted last is output first