introduction
numpy and pytorch provide a variety of methods to distinguish when we want to calculate a vector or matrix a times b. Let's sort them out today.
radio broadcast
Before that, we must understand the broadcasting mechanism. Both NumPy and PyTorch have broadcast mechanisms.
When the shapes of the two vectors to be operated (not just multiplication) are different, if certain conditions are met, the small vector will be broadcast into a large vector to make their dimensions consistent.
When broadcasting, their shapes are compared element by element. If two vectors a and b have the same shape. So a*b is the multiplication of the corresponding elements.
> a = np.array([1.0, 2.0, 3.0]) > b = np.array([2.0, 2.0, 2.0]) > a * b array([2., 4., 6.])
When two vectors in the operation have different shapes but meet some conditions, the broadcast mechanism will be triggered.
> a = np.array([[ 0, 0, 0],
[10,10,10],
[20,20,20],
[30,30,30]])
> b = np.array([1,2,3]) # (3,) -> (1,3) -> (4,3)
> a + b
array([[ 1, 2, 3],
[11, 12, 13],
[21, 22, 23],
[31, 32, 33]])
The following figure well illustrates the above calculation process:
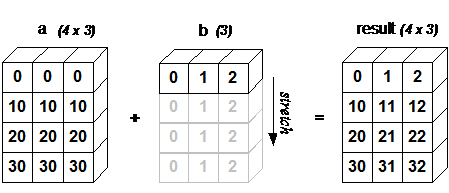
Here b is an array with 3 elements. Add a dimension from the left and change it into ( 1 × 3 ) (1 \times 3) (1 × 3) The vector, then repeated four times in the first dimension, becomes ( 4 × 3 ) (4 \times 3) (4 × 3) Make the dimensions of a and b consistent, and then add the corresponding elements.
Some of the above conditions are: first, make all input arrays align with the array with the longest shape. The insufficient parts in the shape are supplemented by adding 1 to the left of the dimension, and then compare the corresponding dimension values. It needs to meet the following requirements:
- They are equal
- The other one is 1
If this condition is not met, broadcasting cannot be performed.
Theory is always boring and needs to be understood through examples.
Let's take the example above as an example,
a # (4,3) b = np.array([1,2,3]) # (3,) -> (1,3) -> (4,3)
What is the shape of a ( 4 × 3 ) (4 \times 3) (4 × 3) The shape of b is ( 3 , ) (3,) (3), B needs to keep up with A. first, add 1 to the left of its dimension until they have the same number of dimensions (i.e. a.ndim == b.ndim is True), so here it becomes ( 1 , 3 ) (1,3) (1,3);
Compare their first dimension values, a and b, respectively 4 4 4 and 1 1 1. At this time, b repeats this dimension four times to keep up with the boss, and b becomes ( 4 × 3 ) (4 \times 3) (4×3);
Compare their second dimension values, both 3 3 3. They are equal and do nothing;
They have only two dimensions. The comparison is over.
Then add here.
Here are some other examples:
> a = np.arange(4) # (4,) > b = np.ones(5) # (5,) > a + b ValueError: operands could not be broadcast together with shapes (4,) (5,)

Yes, it doesn't make sense. The dimension values of the two are different, so the corresponding elements cannot be added or broadcast.
Let's take a more complex example:
> a = np.arange(4).reshape(4,1) # (4,1)
> b = np.ones(5) # (5,)
> (a + b).shape
(4, 5)
> a + b
array([[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.]])
At first glance, it seems a little strange. Let's analyze it.
What is the shape of a ( 4 × 1 ) (4 \times 1) (4 × 1) The shape of b is ( 5 , ) (5,) (5), b needs to be aligned with a. first, add 1 to the left of its dimension, so here it becomes ( 1 , 5 ) (1,5) (1,5);
Compare their first dimension values, a and b, respectively 4 4 4 and 1 1 1. At this time, b repeats this dimension four times to keep up with boss a, and b becomes ( 4 × 5 ) (4 \times 5) (4×5);
Compare their second dimension values, a and b, respectively 1 1 1 and 5 5 5. Hey, at this time, b salted fish turns over and becomes the object to be looked up to. A is in line with b. A repeats 5 times in this dimension, and a becomes ( 4 × 5 ) (4 \times 5) (4×5)
They have only two dimensions. The comparison is over.
Then add here.

Let's perform the above example through manual broadcasting.
# Let's see what a and b look like first
> a
array([[0],
[1],
[2],
[3]])
> b
array([1., 1., 1., 1., 1.])
> a_new = np.repeat(a, repeats=5, axis=1) # a it needs to be repeated 5 times on the second dimension
> a_new # (4,5)
array([[0, 0, 0, 0, 0],
[1, 1, 1, 1, 1],
[2, 2, 2, 2, 2],
[3, 3, 3, 3, 3]])
Look at the b-to-b conversion.
> b_new = b[np.newaxis, :] # Now insert a dimension on the left and it becomes (1,5)
> b_new
array([[1., 1., 1., 1., 1.]])
> b_new = np.repeat(b_new, repeats=4,axis=0) # Then it is repeated 4 times on the first dimension and becomes (4,5)
> b_new
array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
Their dimensions are consistent, and now you can add by element.
> a_new + b_new
array([[1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4.]])
> (a_new + b_new ) == (a + b) # Verify it
array([[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True]])
Numpy
Numpy provides many methods for multiplication calculation, mainly including numpy.dot, numpy.matmul and numpy.multiply.
np.dot
numpy.dot(a,b)
Dot multiplication of two arrays
- If both a and b are one-dimensional (1-D) arrays, calculate their inner product
- If both a and b are two-dimensional (2-D) arrays, the matrix product is calculated. At this time, it is recommended to use matmul or a @ b
- If a or B is scalar (0-D) and equivalent to multiply, numpy.multiply(a,b) or a * b is recommended
- If a is an N-dimensional (N-D) array and b is a one-dimensional array, it is to calculate the inner product on the last dimension (axis) of a and b (multiply and sum by elements)
- If a is an N-dimensional array and b is an m-dimensional (M-D, M > = 2) array, it is the inner product of the last dimension (axis) of a and the penultimate dimension of b (multiplication and summation of corresponding elements)
> np.dot(3, 4) # Two scalars, equivalent to a*b 12 > a = np.arange(3) # [0 1 2] > b = np.arange(3,6) # [3 4 5] > print(a,b) [0 1 2] [3 4 5] > print(np.dot(a,b)) # 0 * 3 + 1 * 4 + 2 * 5 = 14 two one-dimensional arrays, calculate their inner product 14 > a = np.arange(6).reshape(-1,2) # (3,2) > b = np.arange(2).reshape(2,-1) # (2,1) > print(a) [[0 1] [2 3] [4 5]] > print(b) [[0] [1]] > print(np.dot(a,b)) # (3,2) x (2,1) - > (3,1) two two-dimensional arrays to calculate matrix multiplication [[1] [3] [5]]
Let's look at the fourth case, which is a little more complicated
> a = np.arange(1,7).reshape(-1,3) #(2,3) a is a two-dimensional array [[1 2 3] [4 5 6]] > b = np.array([1,2,3]) # (3) B is a one-dimensional array [1 2 3] > c = np.dot(a,b) # Calculate the sum of the inner products on the last axis of a and b [14 32]
It is equivalent to using the last axis of a, the axis corresponding to 3 in (2,3) to calculate the inner product with the last axis of b and the first axis (3), that is
[1*1 + 2*2 + 3*3, 4*1 + 5*2 + 6*3] = [14,32]
The most complicated is the last case, because bloggers can't imagine more than three dimensions (if you can imagine it, 🎉, You should be able to understand it very well), so this situation can only be calculated according to the formula provided on the official website, and the specific elements cannot be printed.
In fact, the following example has been simplified into three dimensions. In fact, you can draw a cube matrix. What is said above is an excuse, mainly laziness.
a = np.arange(3*4*5).reshape((3,4,5)) # (3,4,5) b = np.arange(5*6).reshape((5,6)) #(5,6)
A is a three-dimensional array, B is a two-dimensional array, and np.dot(a,b) is the inner product of the last dimension (axis) of a and the penultimate dimension of B (multiplication and summation of corresponding elements)
> c = np.dot(a, b) # (3,4,5) (5,6) ⚠️ The number of elements on the last axis of a is 5, and the number of elements on the penultimate axis of b is also 5 > print(c.shape) (3, 4, 6)
sum(a[i,j,:] * b[:,m]) -> [i,j,m]
Mainly through the above calculation, it is proved that:
print(c[2,3,5]) # 4905 print(sum(a[2,3,:] * b[:,5])) # 4905
In fact, the formula given on the official website is as follows:
dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m]) -> [i,j,k,m]
I thought the four-dimensional was a little complicated, so I changed it to three-dimensional.
In order to understand a complex knowledge point, we should simplify the complex problem, grasp the main context (Law), and expand after understanding it. Similar to reading the source code, we should first clarify the main processes. Some tributaries, such as exception handling and calling a complex function implementation, can be ignored first.
This is the calculation formula. I can't think of the application scenario for the time being.
Therefore, for the readability of the code, it is recommended to use np.dot only when they are all one-dimensional arrays, and use the corresponding recommended function in other cases. Maybe that's why torch simplifies this.
np.matmul
numpy.matmul(a,b)
Calculate the matrix product of two arrays:
-
If both are 2-D arrays, it's like our common matrix multiplication
-
If the dimension of any parameter is n-D (n > 2), it will be regarded as a stack of matrices in the last two dimensions and broadcast accordingly.
-
If the dimension of a is 1-D, it will be promoted to a matrix by inserting 1 into its dimension on the left, and then multiply it with b. after that, the inserted 1 will be removed
-
If the dimension of b is 1-D, it will be promoted to a matrix by inserting 1 into its dimension on the right, and then multiply it with A. after that, the inserted 1 will be removed
There are two main differences between matmul and dot:
- Multiplication with scalar is not allowed. Use * instead
- Matrix stack, broadcast by element: (n, K) x (k, m) - > (n, m)
Case 1:
> a = np.array([[1, 0],
[0, 1]])
> b = np.array([[4, 1],
[2, 2]])
> np.matmul(a, b) # The first line is [1 * 4 + 0 * 2, 1 * 1 + 0 * 2] = [4,1]
array([[4, 1],
[2, 2]])
Qingxing 2:
> a = np.arange(2 * 2 * 4).reshape((2, 2, 4)) > b = np.arange(2 * 2 * 4).reshape((2, 4, 2)) > np.matmul(a,b).shape # (2,2,4)x (2,4,2) -> (2,2,2) (2, 2, 2)
For a, it is regarded as two 2 × 4 2 \times 4 two × Stacking of matrices of 4;
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
Similarly, for b, it will also be regarded as two 4 × 2 4 \times 2 four × Stack of matrices of 2.
array([[[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7]],
[[ 8, 9],
[10, 11],
[12, 13],
[14, 15]]])
Therefore, np.matmul(a,b) multiplies the first matrix of a and the first matrix of B, multiplies the second matrix of a and the second matrix of B, and finally obtains one 2 × 2 × 2 2 \times 2 \times 2 two × two × 2 matrix.
Scenario 3:
> a = np.array([1, 2]) # (2,) - > (1,2) it is like executing the following code a = a[np.newaxis,...]
> b = np.array([[1, 0],
[0, 1]]) # (2,2)
> np.matmul(a, b) # (1,2) x (2,2) -> (1,2) -> (2,)
array([1, 2])
Scenario 4:
> a = np.array([[1, 0],
[0, 1]]) # (2,2)
> b = np.array([1, 2]) #(2,) -> (2,1)
> np.matmul(a, b) # (2,2) x (2,1) -> (2,1) -> (2,)
array([1, 2])
Cannot multiply with scalar:
> np.matmul([1,2], 3) --------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-36-33405c3e27ac> in <module>() ----> 1 np.matmul([1,2], 3) ValueError: matmul: Input operand 1 does not have enough dimensions (has 0, gufunc core with signature (n?,k),(k,m?)->(n?,m?) requires 1)
Matrix stack, broadcast by element.
> a = np.arange(2*2*4).reshape((2,2,4)) > b = np.arange(2*4).reshape((4,2)) # (4,2) -> (1,4,2) --Repeat--> (2,4,2) > np.matmul(a, b).shape #(2,2,4) x (2,4,2) -> (2,2,2) (2, 2, 2)
This involves broadcast operations.
First, b will insert dimension 1 from the leftmost side until the number of dimensions is consistent with (a); Then copy b once and stack it to make its dimension consistent with a; Finally, the calculation of case 2 is carried out.
💡 You can use @ instead of np.matmul. For example, it can be written as:
> a @ b
array([[[ 28, 34],
[ 76, 98]],
[[124, 162],
[172, 226]]])
numpy.multiply
numpy.multiply(x1,x2)
Perform element by element multiplication on two parameters (corresponding element multiplication). If they are different in shape, they must be broadcast to match the dimensions.
> np.multiply(2.0, 4.0)
8
> x1 = np.arange(9.0).reshape((3, 3)) # (3,3)
> x1
array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]])
> x2 = np.arange(3.0) # (3,) -> (1,3) --Repeat--> (3,3)
array([0., 1., 2.])
> np.multiply(x1, x2) # (3,3) x (3,3) -> (3,3)
array([[ 0., 1., 4.],
[ 0., 4., 10.],
[ 0., 7., 16.]])
Here is another explanation of the repeat in the broadcast. It is copied twice and stacked together, as follows:
> x2_new = np.array([x2,x2,x2])
> x2_new
array([[0., 1., 2.],
[0., 1., 2.],
[0., 1., 2.]])
Let's multiply and verify:
> np.multiply(x1, x2_new)
array([[ 0., 1., 4.],
[ 0., 4., 10.],
[ 0., 7., 16.]])
💡 You can use * instead of np.multiply.
OK, let's discuss NumPy's multiplication first. Let's look at the multiplication commonly used in PyTorch.
Torch
PyTorch also provides many methods for multiplication calculation, mainly discussing torch.dot, torch.match, torch.mm and torch.bmm.
torch.dot
⚠️ Unlike numpy, a and b must be one-dimensional vectors with the same number of elements.
> a = torch.tensor([2, 3]) > b = torch.tensor([2, 1]) > print(a.shape) torch.Size([2]) > print(b.shape) torch.Size([2]) > print(torch.dot(a,b)) # 2x2 + 3x1 tensor(7)
torch.dot is very simple, and torch.match will be more complex. It is equivalent to moving the relevant features in np.dot to this method.
torch.matmul
torch.matmul(a,b)
Matrix multiplication of two tensors.
The result of the multiplication depends on the shape of the two tensors:
- If they are all one-dimensional, return their inner product, and the result is a scalar.
- If both are two-dimensional, return the matrix product.
- If a is one-dimensional and b is two-dimensional, a will be promoted to a matrix by inserting 1 into its dimension on the left, and then matrix multiplication will be performed. After that, the inserted dimension will be removed.
- If a is two-dimensional and b is one-dimensional, the matrix vector multiplication result is returned.
- If both parameters are at least one-dimensional and at least one parameter is N-dimensional (where N > 2), a batched matrix multiplication is returned. If a is one-dimensional, for batch matrix multiplication, add 1 to the left of the dimension, and then delete dimension 1. If b is one-dimensional, add 1 to the right of its dimension and delete it. Non matrix dimensions (i.e. batch) are broadcast.
Let's look at it one by one.
Case 1:
# vector x vector > a = torch.randn(3) > b = torch.randn(3) > torch.matmul(a, b).size() # Get a scalar torch.Size([])
Scenario 2:
# matrix x matrix > a = torch.randn(3,2) > b = torch.randn(2,4) > torch.matmul(a,b).size() # (3,2) x (2,4) -> (3,4) torch.Size([3, 4])
Scenario 3:
# vector x matrix > a = torch.randn(3) # (3) -> (1,3) > b = torch.randn(3,4) # (3,4) > torch.matmul(a,b).size() # (1,3) x (3,4) -> (1,4) -> (4) torch.Size([4])
Scenario 4:
# matrix x vector > a = torch.randn(3, 4) # (3,4) > b = torch.randn(4) # -> (4,1) > torch.matmul(a, b).size() # (3,4) x (4,1) -> (3,1) -> (3) torch.Size([3])
Case 5 - batch matrix ✖️ Broadcast vector
# batched matrix x broadcasted vector > a = torch.randn(10, 3, 4) # (10,3,4) is equivalent to 10 (3,4) matrices > b = torch.randn(4) # (4,1) - > (10,4,1) will copy the matrix of (4,1) 9 times to obtain 10 identical (4,1) matrices > torch.matmul(a, b).size() #(10,3,4) x (10,4,1) -> (10,3,1) -> (10,3) torch.Size([10, 3])
Case 5 - batch matrix ✖️ Batch matrix
# batched matrix x batched matrix > a = torch.randn(10, 3, 4) # (10,3,4) is equivalent to 10 (3,4) matrices > b = torch.randn(10, 4, 5) # (10,4,5) is equivalent to 10 (4,5) matrices > torch.matmul(a, b).size() # (10,3,4) x (10,4,5) - > (10,3,5) get 10 (3,5) matrices torch.Size([10, 3, 5])
Case 5 - batch matrix ✖️ Broadcast matrix
# batched matrix x broadcasted matrix > a = torch.randn(10, 3, 4) # (10,3,4) > b = torch.randn(4, 5) # (4,5) -> (10,4,5) > torch.matmul(a, b).size() # (10,3,4) x (10,4,5) -> (10,3,5) torch.Size([10, 3, 5])
It can be seen that in case 5, a parameter is first converted into a matrix, and then matrix operation is performed. For (10,3,4) this dimension can be understood as 10 (3,4) matrices stacked, or 10 (3,4) matrices in the batch.
⚠️ Broadcast logic is only applied to batch dimension, not matrix dimension. For example, a is a ( j × 1 × n × m ) (j\times 1 \times n \times m) (j × one × n × m) Then b is a tensor ( k × m × p ) (k\times m \times p) (k × m × p) The tensor of. Here is the batch dimension ( j × 1 ) (j \times 1) (j × 1) And ( k ) (k) (k) Can be broadcast, both broadcast as ( j × k ) (j \times k) (j × k) Therefore, the final result is ( j × k × n × p ) (j \times k \times n \times p) (j×k×n×p).
> a = torch.randn(10, 1, 3, 4) # Matrix dimension (3,4), batch dimension (10,1), broadcast as (10,2) > b = torch.randn(2, 4, 5) # Matrix dimension (4,5), batch dimension (2), broadcast as (10,2) > torch.matmul(a, b).size() # (10,2,3,4) x (10,2,4,5) -> (10,2,3,5) torch.Size([10, 2, 3, 5])
torch.mm
torch.mm(a,b)
Matrix multiplication is performed on these two matrices.
If a is ( n × m ) (n \times m) (n × m) Tensor, b is ( m × p ) (m \times p) (m × p) Tensor, the result is ( n × p ) (n \times p) (n × p) Tensor of.
⚠️ This function does not support broadcasting.
> a = torch.randn(2, 3) > b = torch.randn(3, 3) > torch.mm(a, b).size() # (2,3) torch.Size([2, 3])
torch.bmm
torch.bmm(a,b)
Perform a batch matrix matrix multiplication.
Both parameters must be 3-D tensors and contain the same number of matrices (the same number of batches).
If a is a ( b × n × m ) (b\times n \times m) (b × n × m) The tensor of B is one ( b × m × p ) (b \times m \times p) (b × m × p) The tensor of the output is ( b × n × p ) (b\times n \times p) (b × n × p) Tensor of.
⚠️ This function also does not support broadcasting.
> a = torch.randn(10, 3, 4) > b = torch.randn(10, 4, 5) > torch.bmm(a, b).size() torch.Size([10, 3, 5])
Reference
- NumPy official document
- PyTorch official document
- Numpy radio