Article catalog
1, Bubble sorting
Basic idea:
In a group of numbers to be sorted, compare and adjust the two adjacent numbers from top to bottom for all the numbers within the range that have not been sorted, so that the larger number sinks and the smaller number rises. That is, whenever two adjacent numbers are compared and their sorting requirements are found to be opposite, they will be exchanged. The effect of each sorting is to sink the elements that do not sink.
Main ideas:
1. Compare adjacent elements. If the first one is bigger than the second, exchange them.
2. Do the same for each adjacent element, from the first pair to the end of each pair. At this point, the last element should be the largest number.
3. Repeat the above steps for many elements except the last one.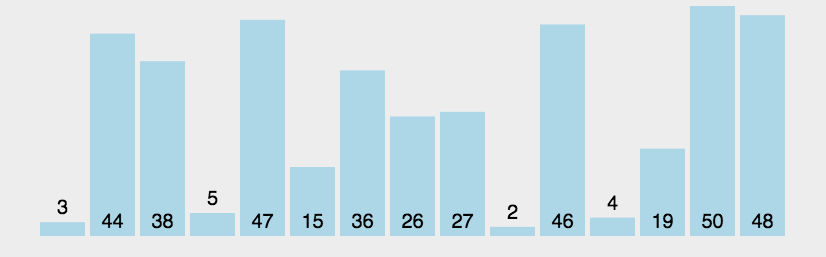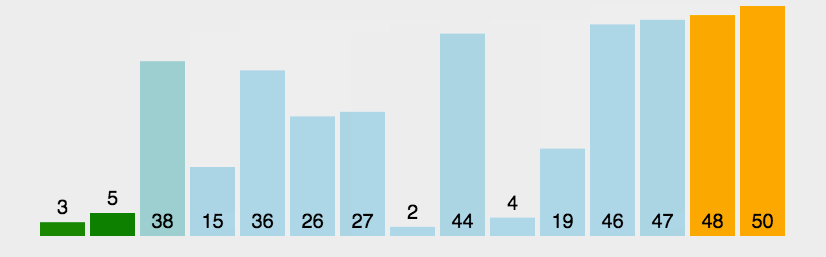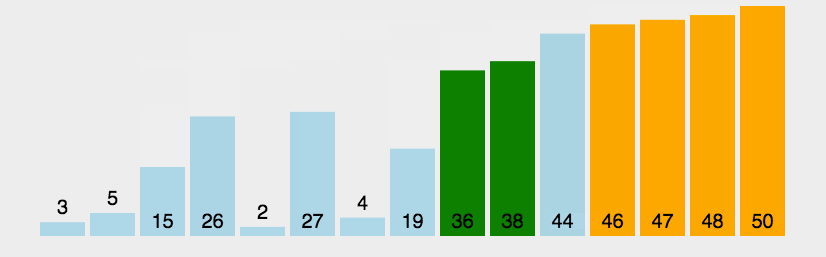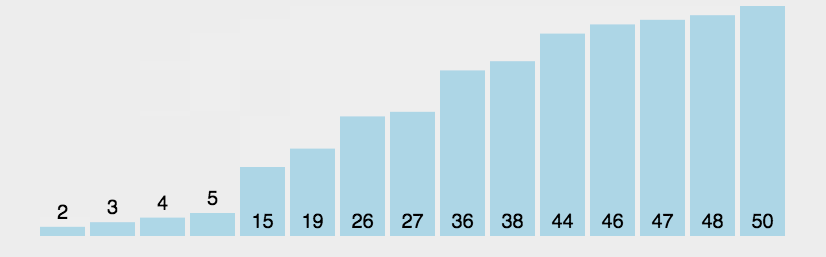
Code example:
//Bubble sorting***********************************
void bubble_sort(int arr[], int n)
{
int temp = 0;//Save intermediate value
for (int i = 0; i <n-1; i++) //Number of sortings n-1
{
for (int j =0; j <n-1-i; j++) //After walking in pairs, put the largest one in the back
{
if (arr[j] > arr[j+1])
{
temp = arr[j+1];
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
}
//Another way of writing*************
void bubble_sort1(int arr[], int n)
{
int temp = 0;//Save intermediate value
for (int i = 0; i < n - 1; i++) //From the first, compare 1 and 2, 1 and 3... 2 and 3
{
for (int j = i + 1; j < n; j++)
{
if (arr[i] > arr[j])
{
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
}
int main()
{
int n;
printf("Please enter the array length:");
scanf("%d", &n);
int* p=(int*)malloc(n * sizeof(int));
printf("Please enter data to be queued:");
for (int i = 0; i < n; i++)
{
scanf("%d", &p[i]);
}
bubble_sort(p, n);
//bubble_sort1(p, n);
printf("Sorted as:");
for (int i = 0; i < n; i++)
{
printf("%d ", p[i]);
}
free(p);
return 0;
}Program implementation:

2, Select sort
Basic idea:
Selection sort is a simple and intuitive sorting algorithm. Its working principle: first, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence, then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence. And so on until all elements are sorted.
Main ideas:
1. First, find the smallest (largest) element in the unordered sequence and store it at the beginning of the sorted sequence.
2. Continue to find the smallest (large) element from the remaining unordered elements, and then put it at the beginning of the unordered sequence.
3. Repeat step 2 until all elements are sorted.
Code example:
void selection_sort1(int arr[], int n)
{
int temp = 0;//Save intermediate value
for (int i = 0; i < n - 1; i++)
{
int mindex = i;//Suppose the first element is the smallest
for (int j = i + 1; j < n; j++)
{
if (arr[mindex] > arr[j])
{
mindex = j;
}
}
temp = arr[mindex];
arr[mindex] = arr[i];
arr[i] = temp;
}
}
int main()
{
int n;
printf("Please enter the array length:");
scanf("%d", &n);
int* p = (int*)malloc(n * sizeof(int));
printf("Please enter data to be queued:");
for (int i = 0; i < n; i++)
{
scanf("%d", &p[i]);
}
selection_sort1(p, n);
printf("Sorted as:");
for (int i = 0; i < n; i++)
{
printf("%d ", p[i]);
}
free(p);
return 0;
}Program implementation:

3, Insert sort
Basic idea:
The unordered sequence to be sorted is regarded as an ordered sequence containing only one element and an unordered sequence. The elements in the unordered sequence are inserted into the ordered sequence one by one, so as to obtain the final ordered sequence.
Main ideas:
Insertion sorting is the simplest and most common method. The array is divided into two parts, the ordered sequence and the unordered sequence. The elements in the unordered sequence are compared with the ordered sequence, and then the elements are inserted into the appropriate position in the ordered sequence.
1. Starting from the first element, the element can be considered to have been sorted
2. Remove an element temp and scan from the sorted element sequence from back to front
3. If the element is larger than tem, move the element to the next bit
4. Repeat step 3 until you find an element less than or equal to temp in the sorted elements
5. Insert temp after the element. If all sorted elements are greater than temp, insert temp at the position with subscript 0
6. Repeat steps 2 to 5
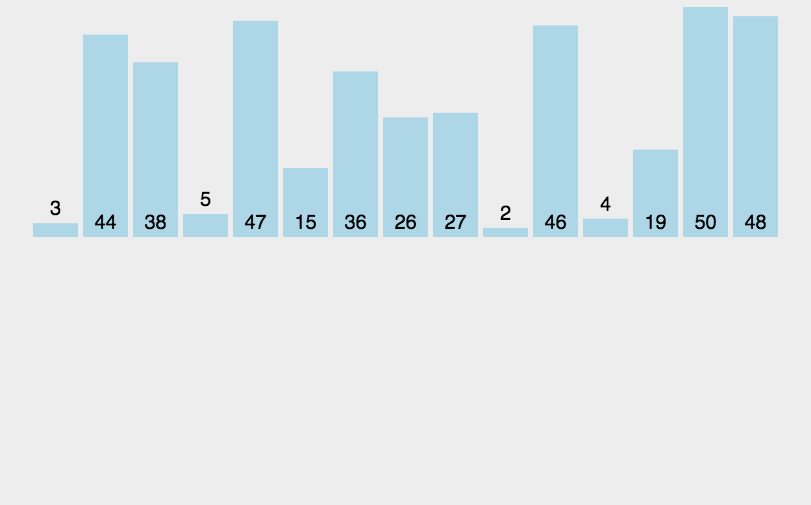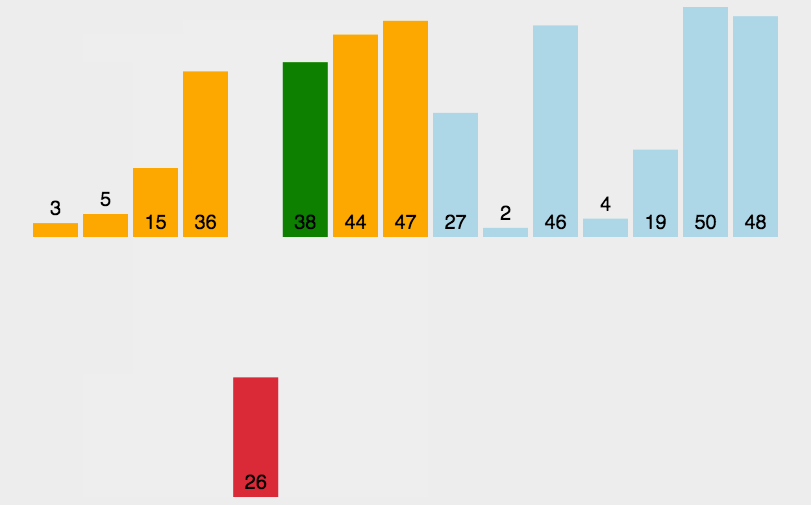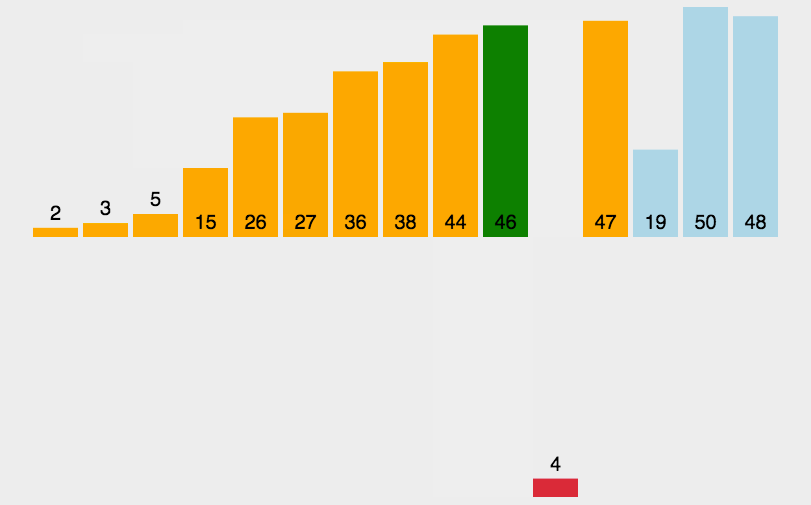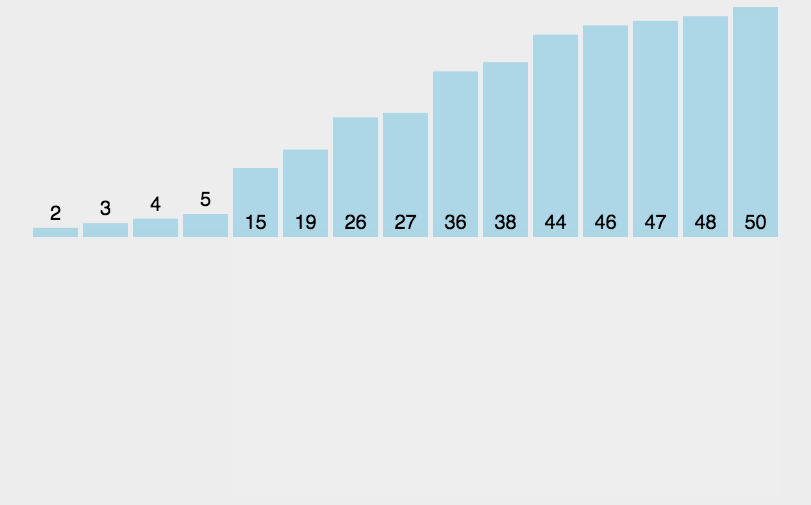
Illustration:
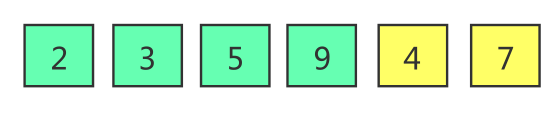
Light green represents the ordered part and yellow represents the disordered part.
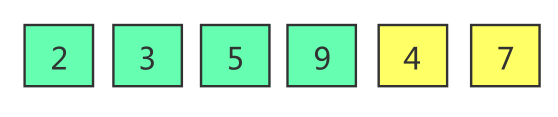
Pick out the elements to be inserted into the ordered part in the unordered part
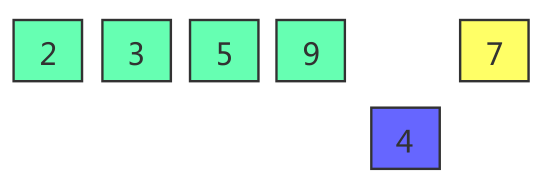
Compare the element to be inserted with the element of the nearest ordered part on the left. Since 4 < 9, 9 moves backward and 4 moves forward
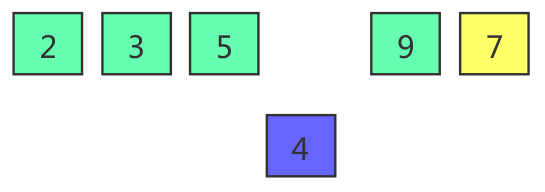
Continue to compare the element to be inserted with the element of the nearest ordered part on the left. Since 4 < 5, 5 moves backward and 4 continues to move forward
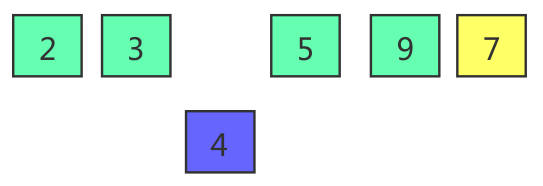
Continue to compare 4 with 3. Since 4 > 3, it is no longer compared forward and inserted into the current position

At this time, the ordered part changes from [2,3,5,9] to [2,3,4,5,9]
Code example:
void Input(int arr[], int n) //Input function
{
printf("Please enter data to be queued:");
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i]);
}
}
void Show(int arr[], int n) //Print function
{
printf("Sorted as:");
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
}
//Insert sort**********************
void Insert(int arr[], int n)
{
int i;
int j;
int temp;//Save the element to insert
for (i = 1; i < n; i++)//The first element is regarded as ordered, and the subsequent elements are inserted into the front one by one
{
temp = arr[i];
j = i - 1; //Start with the previous element to insert
while (j >= 0)
{
if (arr[j] > temp) //Move back larger than the element to insert
{
arr[j + 1] = arr[j];//The front element moves back
j--;
}
else //Smaller than the inserted element, exit while
break;
}
arr[j + 1] = temp; // Insert the element to be inserted into the corresponding position
}
}
int main()
{
int n;
printf("Please enter the array length:");
scanf("%d", &n);
int* p = (int*)malloc(n * sizeof(int));
Input(p, n);
Insert(p, n);
Show(p, n);
free(p);
return 0;
}Program demonstration:

Insert sort optimization
Split insertion sorting: this kind of optimization has the idea of dichotomy. When comparing the elements to be sorted with the elements of the ordered part, it is no longer compared one by one, but compared in a binary compromise way to speed up the comparison efficiency.
Code example:
//Insert sort using dichotomy
void BinaryInsert(int arr[],int n)
{
int j;
int low, mid, high;
int temp; //Save the number of to insert each time
for (int i = 1; i < n; i++)
{
low = 0;
high = i - 1;
temp = arr[i];
/*Find the appropriate insertion position high+1 if the middle position element
*If it is larger than the element to be inserted, the search area moves to the lower half area. No
*Move to the upper half
*/
while (low <= high)
{
mid = (low + high) / 2;
if (arr[mid] > temp)
{
high = mid - 1;
}
else
low = mid + 1;
}
//Move elements back after high+1
for (j = i - 1; j >= high + 1; j--)
{
arr[j + 1] = arr[j];
}
//Inserts the element into the specified location
arr[j + 1] = temp;
}
}4, Merge sort
Basic idea:
Merge sort is an effective sort algorithm based on merge operation
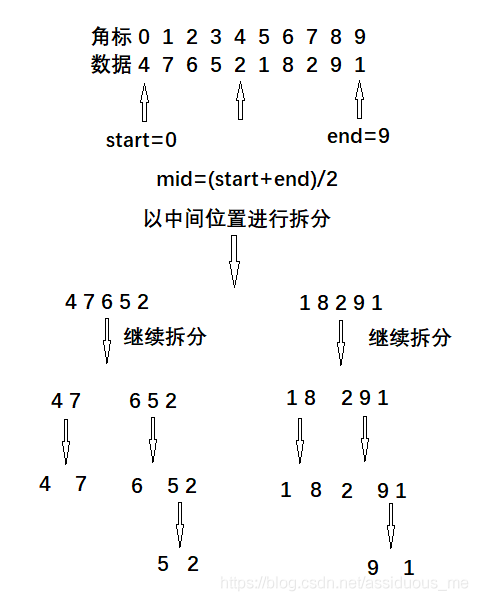
Divide and Conquer is a very typical application. The ordered subsequences are combined to obtain
Completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If you merge two ordered tables into
An ordered table is called two-way merging.
Split:
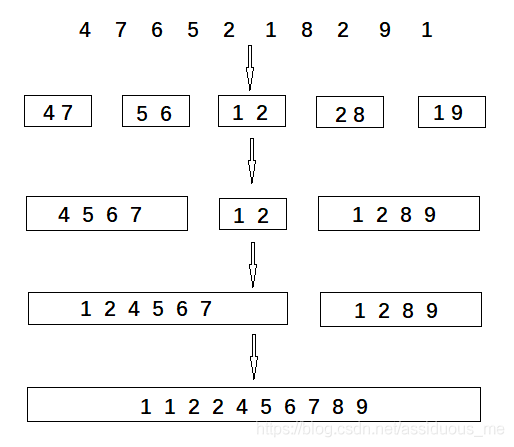
Consolidation:
Main ideas:
Merge sort, which literally means merging arrays, so what should we do?
If there are two sorted arrays {1,3,4,8}, {2,6,9,12};
We'll merge and sort the two arrays;
The target array should be {1,2,3,4,6,8,9,12};
Does that mean that we should sort the array {1,4,6,8,2,7,9,12} from small to large into the target array;
Now let's realize it!
We use i to represent the first element 1 in {1,3,4,8}; The first element 2 in {2,6,9,12} is represented by j;
k is used to represent the new array, that is, the first element of the array to be sorted; Then the important came!
Judge the size of i and j;
If I < J, let k=i; i++,k++;
If I > J, let k=j; j++,k++;
Finally, there must be elements left in an array. For example, 9 and 12 in {2,6,9,12} above will be left. Finally, put 9 and 12 in the array to be sorted!
Therefore, for code implementation, we need the variable left to represent 1, the variable mid to represent 8 and the variable right to represent 12
From left to mid is {1,3,4,8}, and from mid+1 to right is {2,6,9,12}
The above is to merge two ordered arrays. What should we do with unordered arrays? This introduces our idea of partition
If we have an array {5,2,6,1,4,6,3,7} and divide it into two parts to perform the above sorting function, but we will find that {5,2,6,1} and {4,6,3,7} are still not two ordered arrays, then we just need to divide and divide again!!
Finally, it is divided into a pile of arrays with only two elements, which is always satisfied!
Then we need to recursively call the opening and closing functions
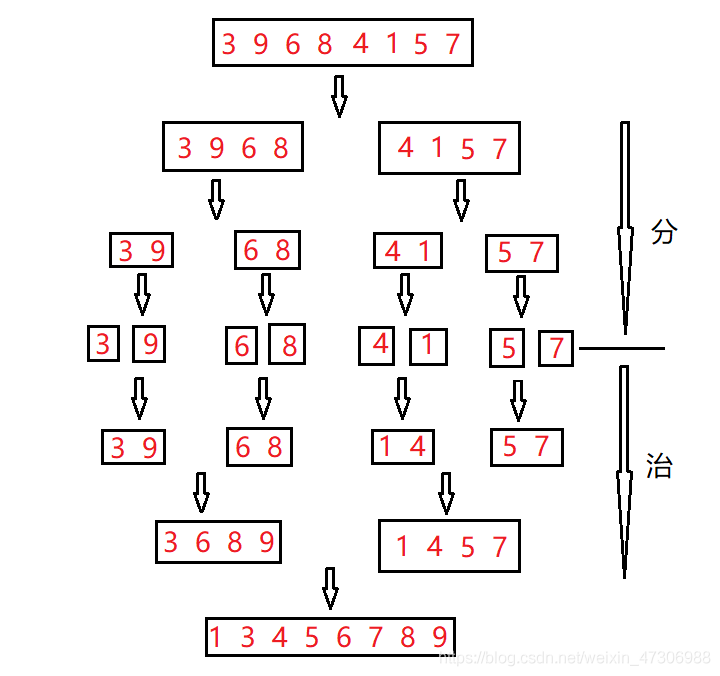
Here is a code example:
void merge(int arr[],int brr[],int left, int mid, int right) //merge
{
int i, j, k;
i = left; //Marks the first unordered element in the left half
j = mid + 1; //Marks the first unordered element in the right half
k = left; //Temporary array element subscript
//merge
while (i <= mid && j <= right)
{
if (arr[i] <= arr[j])
{
brr[k++] = arr[i++];
}
else
{
brr[k++] = arr[j++];
}
}
//Merge the remaining elements in the left half
while (i <= mid)
{
brr[k++] = arr[i++];
}
//Merge the remaining elements in the right half
while (j<=right)
{
brr[k++] = arr[j++];
}
//The elements in the temporary array are assigned to the original array
for (int l = 0; l < right+1; l++)
{
arr[l] = brr[l];
}
}
//Merge sort
void merge_sort(int arr[],int brr[], int left, int right)
{
//If there is only one element, there is no need to divide
if (left<right)
{
//Find the middle point
int mid = (left + right) / 2;
//Recursive partition of left half region
merge_sort(arr,brr, left, mid);
//Recursive partition of the right half
merge_sort(arr,brr, mid + 1, right);
//Merge sorted parts
merge(arr,brr,left, mid, right);
}
}
//Merge sort entry
void mergesort(int arr[], int n)
{
//Allocate an auxiliary array
int* brr = (int*)malloc(n * sizeof(int));
assert(brr != NULL);
merge_sort(arr,brr,0, n - 1);
if (brr == NULL)
printf("error");
free(brr);
}
int main()
{
int n;
printf("Please enter the array length:");
scanf("%d", &n);
int* p = (int*)malloc(n * sizeof(int));
printf("Please enter data to be queued:");
for (int i = 0; i < n; i++)
{
scanf("%d", &p[i]);
}
mergesort(p,n);
printf("Sorted as:");
for (int i = 0; i < n; i++)
{
printf("%d ", p[i]);
}
free(p);
return 0;
}Program test:

5, Quick sort (left and right pointer method)
Basic idea:
The basic idea of quick sorting algorithm is divide and conquer. First, take a number from the sequence as the axis value (reference number) key;
Divide the number series according to the benchmark number. Those less than the benchmark number are placed on the left and those greater than the benchmark number are placed on the right;
Repeat the partition operation until you know that each interval has only one number.
Main ideas:
1. Select a key, usually the leftmost or rightmost.
2. Define a left and a right. Left goes from left to right and right goes from right to left. (Note: if you select the leftmost data as the key, you need to go right first; if you select the rightmost data as the key, you need to go left first).
3. In the process of walking, if right encounters a number less than key, stop and exchange the values of left and right; Left starts to walk until left encounters a number greater than key, and the contents of left and right are exchanged; Right starts to walk again and goes on like this until left and right finally meet. At this time, the content of the meeting point can be exchanged with the key. (select the leftmost value as the key)
4. At this time, the left side of the key is the number less than the key, and the right side of the key is the number greater than the key
5. Sort the left sequence and right sequence of the key in this single pass again. Repeat this operation until there is only one data in the left and right sequences or the left and right sequences do not exist. At this time, this part is in order.
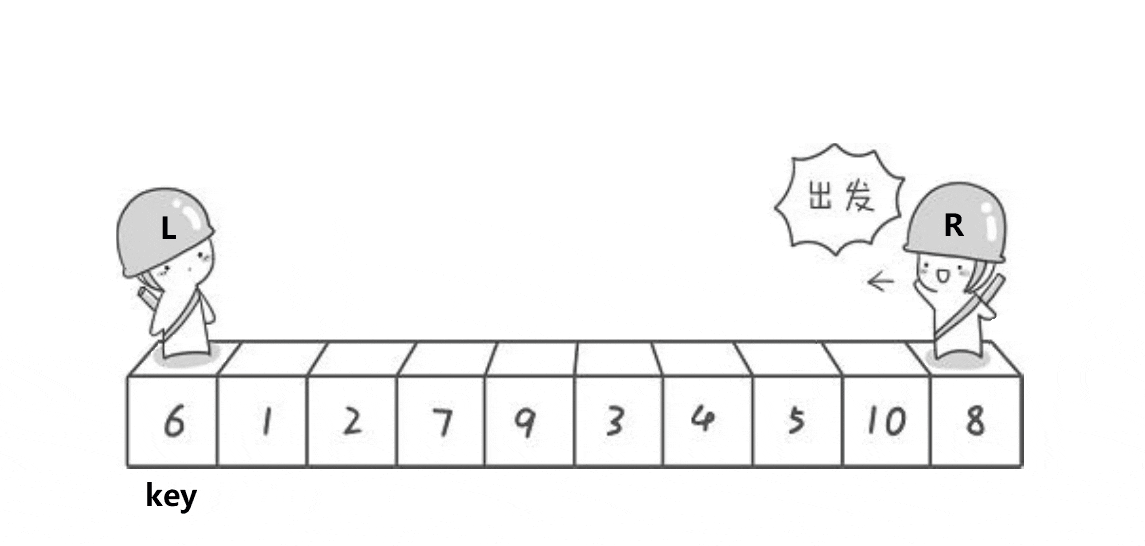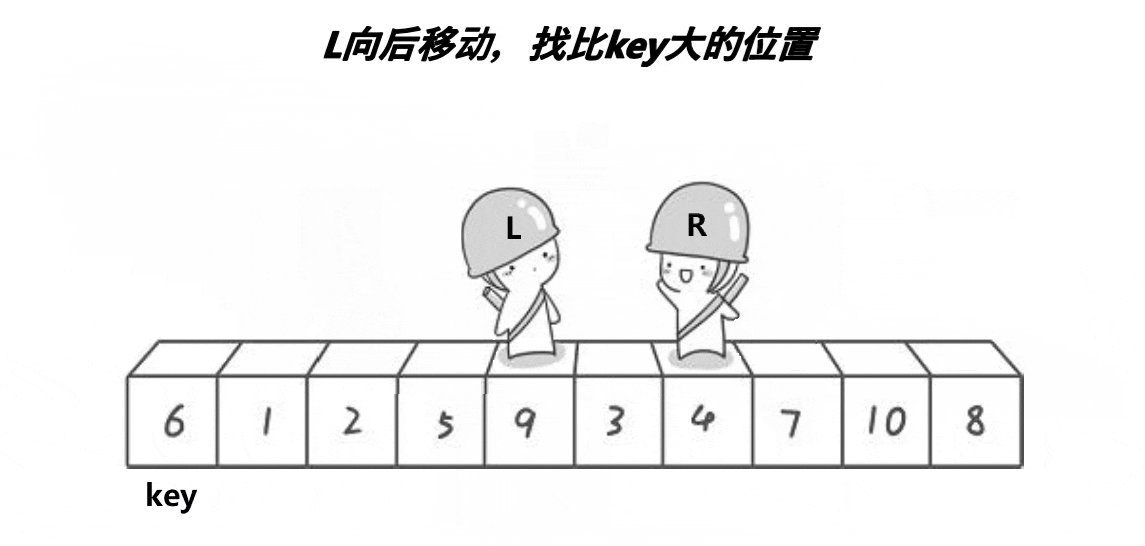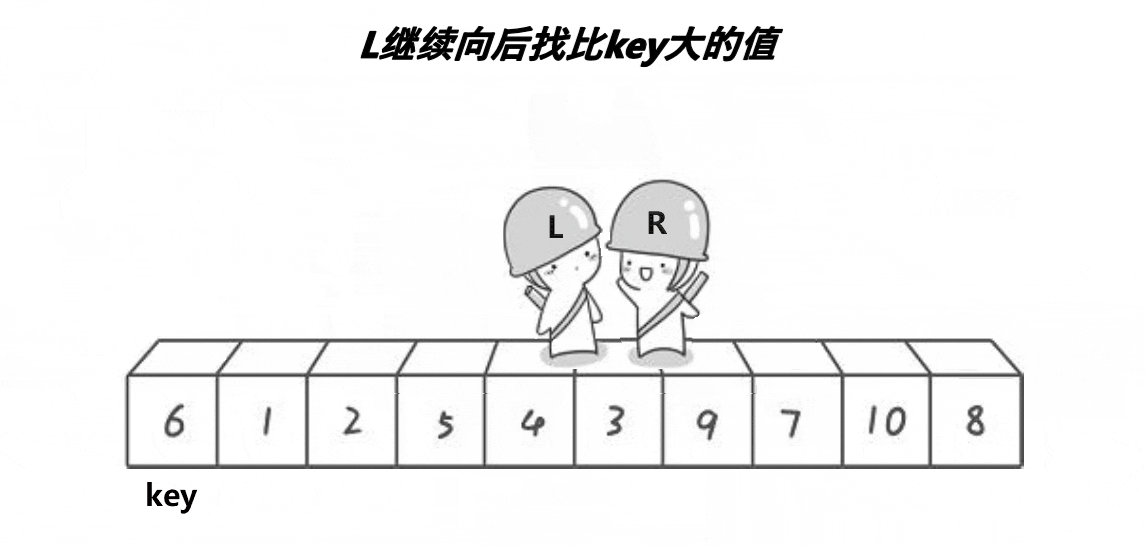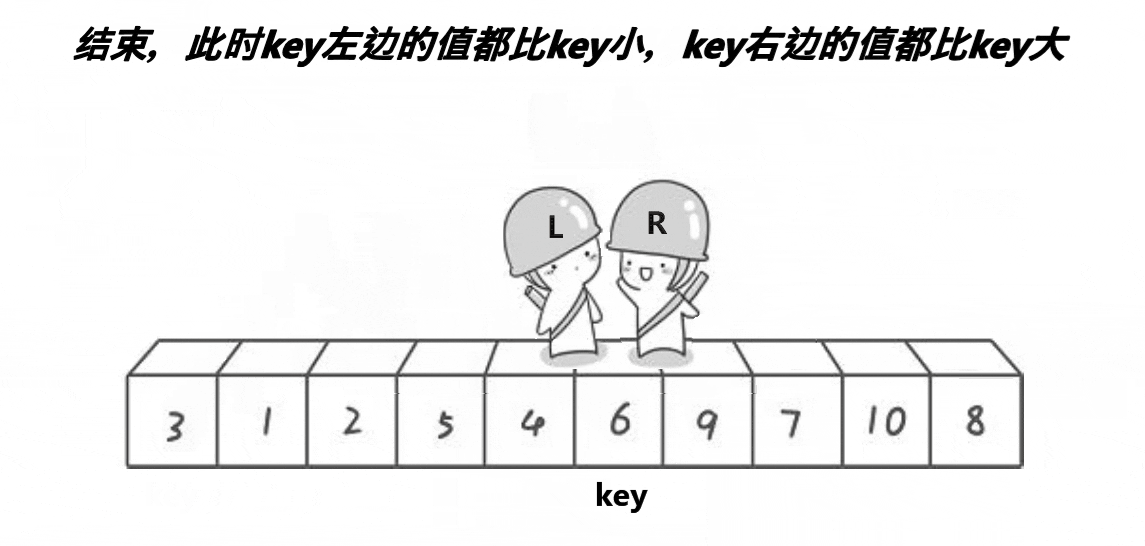
Illustration:
Assign the first number 23 of the array to the temp variable, the pointer i points to the first element of the array, and the pointer j points to the last element of the array

Start traversing from j (from right to left). When 13 is encountered, because 13 < = temp, fill arr[j] into arr[i], that is, the number pointed to by pointer I is 13

Then traverse from I (from left to right). When 45 is encountered, because 45 > temp, fill arr[i] into arr[j]. At this time, the number pointed by pointer j is 45

Continue to traverse from j. when 11 is encountered, because 11 < = temp, fill arr[j] into arr[i], that is, the number pointed to by pointer I is 11

When traversing from I, 89 is encountered. Because 89 > temp, arr[i] is filled in arr[j]. At this time, the number pointed to by pointer j is 89

When traversing from j, when 17 is encountered, because 17 < = temp, fill arr[j] into arr[i], that is, the number pointed to by pointer I is 17

When traversing from j and encountering 3, because 3 < = temp, fill arr[j] into arr[i], that is, the number pointed to by pointer I is 3

When traversing from I to 26, because 26 > temp, fill arr[i] into arr[j]. At this time, the number pointed by pointer j is 26

Traversal from j, and i coincide

take temp (reference number 23) is filled in arr[i]
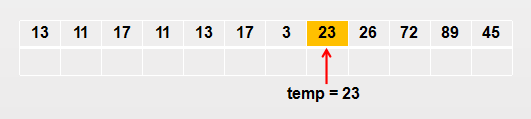
At this time, the second step of the algorithm is completed. Next, the sub intervals on the left and right of 23 are sorted by the above method respectively until there is only one element in the interval, that is, the sorting is completed.
I believe you should have understood the fast scheduling algorithm here
Final code example:
void Input(int arr[], int n) //Input function
{
printf("Please enter data to be queued:");
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i]);
}
}
void Show(int arr[], int n) //Print function
{
printf("Sorted as:");
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
}
//Quick sort left and right pointers
void QuickSort(int* arr, int left, int right)
{
if (left > right)
{
return;
}
int i = left; //Left pointer
int j = right; //Right pointer
int key = arr[i]; //The selection benchmark is usually the first in the array
while (i < j)
{
while (arr[j]>key&&i<j) //When the number on the right is greater than the reference number, skip and continue to search to the left
{ //If the conditions are not met, the loop will jump out. At this time, the element corresponding to j is less than the reference element
j--;
}
if (i < j) //Fill the number of datum elements less than or equal to the right into the corresponding position on the right
{
arr[i] = arr[j];
i++;
}
while (arr[i] < key && i < j) //When the number on the left is less than or equal to the benchmark number, skip and continue to search to the right
{ //If the conditions are not met, the loop will jump out. At this time, the element corresponding to i is greater than or equal to the reference element
i++;
}
if (i < j)
{
arr[j--] = arr[i]; //Fill in the corresponding position on the left with the number greater than the reference element on the left
}
}
arr[i] = key; //Fill the datum element into the corresponding position. At this time, the positions of i and j are equal / / arr[j]=temp
//Recursive call
QuickSort(arr, left, i - 1); //Quick sort the left sub interval of the base element
QuickSort(arr, i + 1, right); //Quick sort the right sub interval of the base element
}
int main()
{
int n;
printf("Please enter the array length:");
scanf("%d", &n);
int* p = (int*)malloc(n * sizeof(int));
Input(p, n);
//Insert(p, n);
//BinaryInsert(p, n);
QuickSort(p, 0, n - 1);
Show(p, n);
free(p);
return 0;
}Program test:

It's not easy to make. If you think it's helpful, please praise it!
