733. Image rendering
simple single \color{#00AF9B} {simple} simple
There is a picture represented by a two-dimensional integer array. Each integer represents the pixel value of the picture, and the value is between 0 and 65535.
Give you a coordinate (sr, sc) to represent the pixel value (row, column) at the beginning of image rendering and a new color value newColor to color the image again.
In order to complete the coloring work, start from the initial coordinates, record the connected pixels with the same pixel value as the initial coordinates in the upper, lower, left and right directions of the initial coordinates, and then record the qualified pixels in the four directions and their corresponding connected pixels with the same pixel value as the initial coordinates in the four directions,... Repeat the process. Change the color values of all recorded pixels to new color values.
Finally, the color rendered image is returned.
Example 1:
input: image = [[1,1,1],[1,1,0],[1,0,1]] sr = 1, sc = 1, newColor = 2 output: [[2,2,2],[2,2,0],[2,0,1]] analysis: Right in the middle of the image,(coordinate(sr,sc)=(1,1)), The color of all eligible pixels on the path is changed to 2. Note that the pixel in the lower right corner is not changed to 2, Because it is not a pixel connected to the initial point in the up, down, left and right directions.
be careful:
- The length of image and image[0] is in the range [1, 50].
- The given initial point will satisfy 0 < = SR < image.length and 0 < = SC < image [0]. Length.
- The color values represented by image[i][j] and newColor are in the range [0, 65535].
preface
We can find that our goal is to traverse the same color Island, and then change the value of each grid in the island to a new value. The islands in this question are the whole composed of directly adjacent or indirectly adjacent same color squares. We can traverse the whole island by using breadth first search or depth first search from any position of the island.
Method 1: breadth first search
We need to record the color of the starting point to judge whether the next node belongs to the same island. If not, skip the node.
We first change the value of the starting point to newColor, and then start breadth first search from the starting point. Assuming that the traversal order is "up, down, left and right" (the order is not important, because the whole island can be traversed at last), that is, search the "up, down, left and right" four squares of the starting point in order. If the color of a grid is the same as the starting point color, modify the color of this grid, and then add it to the queue. and so on.
The reason why queues are needed here is that after modifying the middle grid, we need to record the adjacent same color grids, and then repeat the "up, down, left and right" search operation as the middle grid. In this way, we can traverse the whole island from any position of the island.
We also need a direction array to facilitate us to traverse "up, down, left and right":
-
An array stores changes in the x direction and an array stores changes in the y direction.
/* C++ */ // Left, top, right, bottom const int dy[4] = {-1, 0, 1, 0}; const int dx[4] = {0, -1, 0, 1}; ... for (int i=0;i<4;i++) { int ny = y + dy[i]; int nx = x + dx[i]; } ... -
Just use an array, in which the elements are a pair of values.
/* C++ */ // Left, top, right, bottom const pair<int, int> D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}}; ... for (const direction : D) { int ny = y + direction.first; int nx = x + direction.second; }
notes
- The lengths of image and image[0] are within the range [1,50]. If you want to save space on variables, we can use unsigned char (1 byte).
- The color value is in the range [0, 65535], which is exactly the range that unsigned short int can express (unsigned short int, 2 bytes). We can also use it to replace the int type.
- Only int is OK.
- We need to pay attention to the usual process of traversing a two-dimensional array: first find row i, and then find the value of column J in this row. Think about it, i here is y in coordinates, and j is x in coordinates. In other words, we are looking for the point (x,y) in the plane coordinate system. We should use image[y][x] to locate it, because it is the value in row y and column X. Similarly, sr given in the title is also the Y coordinate, and sc is the X coordinate.
- Similarly to the direction array in the above, the structure is {y coordinate change, x coordinate change}
Process demonstration

#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> dpoint;
typedef unsigned char uc;
typedef unsigned short int usi;
class Solution
{
private:
// Left, top, right, bottom
const dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
vector<vector<int>> floodFill(vector<vector<int>> &image, uc sr, uc sc, usi newColor)
{
uc m = image.size(), n = image[0].size();
usi color = usi(image[sr][sc]);
if (color == newColor)
return image;
image[sr][sc] = newColor;
queue<dpoint> que;
que.emplace(sr, sc);
while (!que.empty())
{
uc y = que.front().first, x = que.front().second;
que.pop();
for (const auto &direction : D)
{
uc ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < m && 0 <= nx && nx < n && image[ny][nx] == color)
{
image[ny][nx] = newColor;
que.emplace(ny, nx);
}
}
}
return image;
}
};
Complexity analysis
-
Time complexity: O(mn), m and n are the number of rows and columns of the two-dimensional array respectively. In the worst case, you need to traverse all the squares once.
-
Spatial complexity: O(mn). The resource occupation in space is mainly the overhead of queue.
Reference results
Accepted 277/277 cases passed (8 ms) Your runtime beats 80.32 % of cpp submissions Your memory usage beats 62.44 % of cpp submissions (13.7 MB)
Method 2: depth first search (recursive)
From the above breadth first search, we can find its characteristics: after traversing all the traversable nodes of the current node, turn to the next node to continue traversal.
The characteristics of depth first search: after traversing a traversable node of the current node, jump to the node immediately. After jumping to the next node, it immediately jumps to a traversable node of the next node, and so on, so it is called depth.
The above characteristics mean breadth and depth. Breadth: fully expand the current node first. Depth: jump to the next node first.
Recursive depth first algorithm is a little easier in thinking. When we traverse a node, we immediately jump to the next node (for example, to the left node); When we return to the node after traversing on the left, we immediately go to the node above. We can think of this process as calling the same function dfs in four loops. We call the dfs function 4 times for each "next node", and each call may jump to the next node. Immediately after the jump, the dfs function 4 times. In this way, it is a recursive depth traversal of all nodes.
The general structure is as follows:
const D[4][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
int main()
{
...
dfs(image, sr, sc);
...
}
void dfs(vector<vector<int>> &image, int y, int x)
{
// maybe do something
for (const auto direction : D)
{
// maybe do something
dfs(image, y+direction[0], x+direction[1]);
}
}
Similarly to method 1, we need to record the color of the starting point to judge whether the next node belongs to the same island. If not, skip the node.
#include <vector>
using namespace std;
typedef pair<int, int> dpoint;
typedef unsigned char uc;
typedef unsigned short int usi;
class Solution
{
private:
const dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
uc m = 0xFF;
uc n = 0xFF;
usi color = 0xFFFF;
usi newColor = 0xFFFF;
public:
vector<vector<int>> floodFill(vector<vector<int>> &image, int sr, int sc, int newColor)
{
this->m = image.size();
this->n = image[0].size();
this->newColor = usi(newColor);
this->color = image[sr][sc];
if (this->color != this->newColor)
{
dfs(image, sr, sc);
}
return image;
}
void dfs(vector<vector<int>> &image, int y, int x)
{
if (image[y][x] == this->color)
{
image[y][x] = this->newColor;
for (const auto &direction : D)
{
uc ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < this->m && 0 <= nx && nx < this->n && image[ny][nx] == color)
{
dfs(image, ny, nx);
}
}
}
}
};
Complexity analysis
-
Time complexity: O(mn), m and n are the number of rows and columns of the two-dimensional array respectively. In the worst case, you need to traverse all the squares once.
-
Spatial complexity: O(mn). Mainly the stack overhead used for recursion.
Reference results
Accepted 277/277 cases passed (4 ms) Your runtime beats 97.87 % of cpp submissions Your memory usage beats 71.56 % of cpp submissions (13.6 MB)
Method 3: depth first search (non recursive)
Unlike breadth first non recursive methods, depth first non recursive methods require stacks. Let's think about why it's arranged like this.
Let's assume that all the node values added in the i round are i, that is, the node value represents the number of rounds it is added in, then after the first round:
- Queue: [1,1,1,1] < - end of queue
- Stack: [1,1,1,1] < - bottom of stack
At the beginning of round 2, since the top of the stack and the head of the team are selected, new elements are added:
- Queue: [1,1,1,2,2,2,2] < - end of queue
- Stack: [2,2,2,2,1,1,1] < - bottom of stack
From here, we can find that due to the characteristics of queue first in first out, the first four rounds of traversal will be 1, that is, the four adjacent nodes of the initial node. This is in line with the concept of "fully expand nodes first" of breadth first. We will get 1,1,1,1,2,2,2,3,3,3.
Due to the characteristics of stack first in and last out, we added four 2 after completing the traversal of the second round of pair 1. Because it was added to the top of the stack, we also took it from the top of the stack in the third round, so we got 2. This is in line with the concept of depth first "looking out first". We will get 2, 3, 4.
As like as two peas, we will take the code of method 1 directly, and then replace the queue with stack.
(optional understanding) we can also focus on more detailed areas. Each element will become the new top of the stack when it is put into the stack. For the nodes traversed in the "top left and bottom right" order set by us, the arrangement of the stack is as follows:
- [bottom, right, top, left] - bottom of stack
Every time we take elements from the top of the stack, the order we get is "bottom right, top left". The order in which we add nodes is "top left, top right and bottom right", and the traversal order becomes "bottom right, top left", which is also the characteristic of the stack.
This is only a detail, which is irrelevant to the subject.
#include <vector>
#include <stack>
using namespace std;
typedef pair<int, int> dpoint;
typedef unsigned char uc;
typedef unsigned short int usi;
class Solution
{
private:
// Left, top, right, bottom
const dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
vector<vector<int>> floodFill(vector<vector<int>> &image, uc sr, uc sc, usi newColor)
{
uc m = image.size(), n = image[0].size();
usi color = usi(image[sr][sc]);
if (color == newColor)
return image;
image[sr][sc] = newColor;
stack<dpoint> stk;
stk.emplace(sr, sc);
while (!stk.empty())
{
uc y = stk.top().first, x = stk.top().second;
stk.pop();
for (const auto &direction : D)
{
uc ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < m && 0 <= nx && nx < n && image[ny][nx] == color)
{
image[ny][nx] = newColor;
stk.emplace(ny, nx);
}
}
}
return image;
}
};
Complexity analysis
-
Time complexity: O(mn), m and n are the number of rows and columns of the two-dimensional array respectively. In the worst case, you need to traverse all the squares once.
-
Spatial complexity: O(mn). The stack can store up to all the land.
Reference results
Accepted 277/277 cases passed (4 ms) Your runtime beats 97.87 % of cpp submissions Your memory usage beats 47.27 % of cpp submissions (13.7 MB)
695. Maximum area of the island
in etc. \color{#FFB800} {medium} secondary
Give you a binary matrix grid of size m x n.
An island is a combination of some adjacent 1s (representing land). The "adjacent" here requires that two 1s must be adjacent in four horizontal or vertical directions. You can assume that the four edges of the grid are surrounded by 0 (representing water).
The area of an island is the number of cells on the island with a value of 1.
Calculate and return the largest island area in the grid. If there are no islands, the return area is 0.
Example 1:
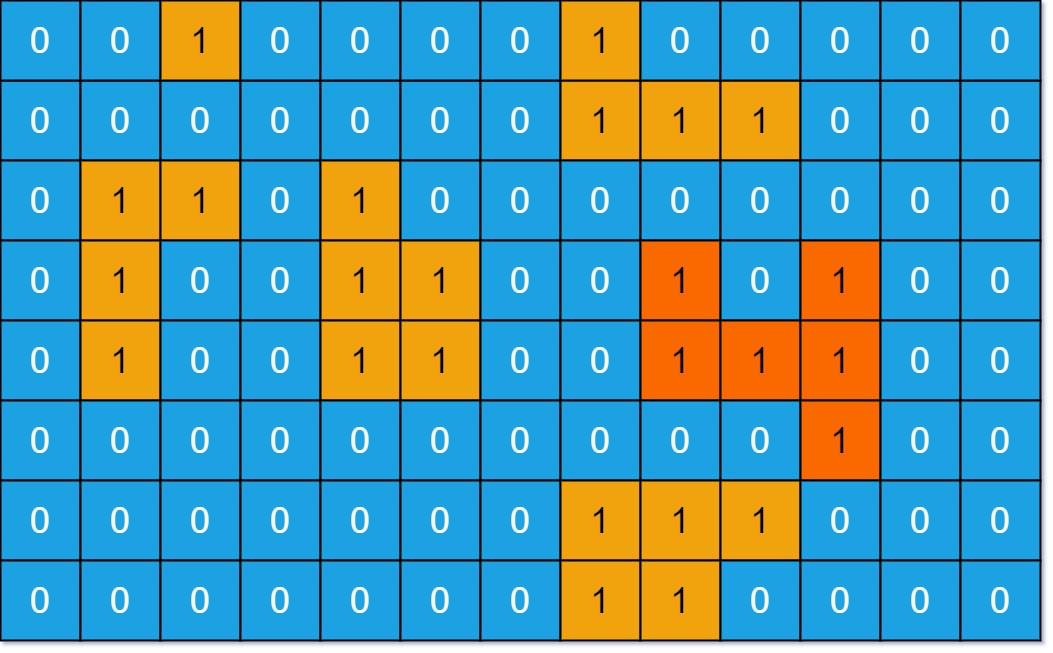
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] Output: 6 Explanation: the answer should not be 11, because the island can only contain 1 in the horizontal or vertical directions.
Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]] Output: 0
Tips:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 50
- grid[i][j] is 0 or 1
preface
There will be multiple islands in this map. In order to find each island, double circulation is necessary. You have to traverse the whole map to make sure you find each island.
In a double loop, we need to find a square with a value of 1. Once we find a square with a value of 1, we find an island. As we can see from the above question, using breadth / depth first, we can traverse the whole island from any position of the island. In the process of traversing the island, we need to change the arrived grid to 0 to avoid repeated stacking / queuing.
So far, the structure of the code is also clear. A loop for stack / queue is embedded in the double loop, or recursive depth first.
As like as two peas, we can see that the problem is almost the same as the last one. The last question is to change the value of the grid in the whole island to newColor. This question is equivalent to changing the color of the island to 0.
The remaining problem is to find the size of the island. This is also very simple. After finding a grid with a value of 1, the initial value of island size area is 1. Then start the breadth / depth first search. Each time a square with a value of 1 is found, the area increases automatically.
Method 1: breadth first search
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> dpoint;
typedef unsigned char uc;
class Solution
{
private:
const dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
int maxAreaOfIsland(vector<vector<int>> &grid)
{
const uc m = grid.size(), n = grid[0].size();
int ans = 0;
for (uc _y = 0; _y < m; _y++)
{
for (uc _x = 0; _x < n; _x++)
{
if (grid[_y][_x] == 0)
continue;
queue<dpoint> que;
que.emplace(_y, _x);
grid[_y][_x] = 0;
int area = 1;
while (!que.empty())
{
uc y = que.front().first, x = que.front().second;
que.pop();
for (const auto &direction : D)
{
uc ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < m && 0 <= nx && nx < n && grid[ny][nx] == 1)
{
que.emplace(ny, nx);
grid[ny][nx] = 0;
area++;
}
}
}
ans = max(ans, area);
}
}
return ans;
}
};
Complexity analysis
-
Time complexity: O(mn), m and n are the number of rows and columns of the two-dimensional array respectively. In the worst case, all the land is an island. The inner loop will traverse once when all lands are set to 0, and the outer loop will traverse once when all islands are traversed (all lands are guaranteed to be 0). A piece of land can be traversed twice at most, so the time complexity is O(2mn)=O(mn).
-
Spatial complexity: O(mn). Mainly the queue overhead.
Reference results
Accepted 728/728 cases passed (16 ms) Your runtime beats 77.64 % of cpp submissions Your memory usage beats 19.24 % of cpp submissions (26.1 MB)
Method 2: depth first search (non recursive)
#include <vector>
#include <stack>
using namespace std;
typedef pair<size_t, size_t> dpoint;
class Solution
{
private:
const dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
public:
int maxAreaOfIsland(vector<vector<int>> &grid)
{
const size_t m = grid.size(), n = grid[0].size();
int ans = 0;
for (size_t _y = 0; _y < m; _y++)
{
for (size_t _x = 0; _x < n; _x++)
{
if (grid[_y][_x] == 0)
continue;
stack<dpoint> stk;
stk.emplace(_y, _x);
grid[_y][_x] = 0;
int area = 1;
while (!stk.empty())
{
size_t y = stk.top().first, x = stk.top().second;
stk.pop();
for (const auto &direction : D)
{
size_t ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < m && 0 <= nx && nx < n && grid[ny][nx] == 1)
{
stk.emplace(ny, nx);
grid[ny][nx] = 0;
area++;
}
}
}
ans = max(ans, area);
}
}
return ans;
}
};
Complexity analysis
-
Time complexity: O(mn), m and n are the number of rows and columns of the two-dimensional array respectively. In the worst case, you need to traverse all the squares once.
-
Spatial complexity: O(mn). The stack can store up to all the land.
Reference results
Accepted 728/728 cases passed (20 ms) Your runtime beats 53.5 % of cpp submissions Your memory usage beats 15.26 % of cpp submissions (26.2 MB)
Method 3: depth first search (recursive)
#include <vector>
using namespace std;
typedef pair<size_t, size_t> dpoint;
class Solution
{
private:
const dpoint D[4] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
size_t m = 0, n = 0;
public:
int maxAreaOfIsland(vector<vector<int>> &grid)
{
this->m = grid.size(), this->n = grid[0].size();
int ans = 0;
for (size_t y = 0; y < m; y++)
{
for (size_t x = 0; x < n; x++)
{
if (grid[y][x] == 1)
ans = max(ans, dfs(grid, y, x));
}
}
return ans;
}
int dfs(vector<vector<int>> &grid, size_t y, size_t x)
{
grid[y][x] = 0;
int ans = 1;
for (const auto &direction : D)
{
size_t ny = y + direction.first, nx = x + direction.second;
if (0 <= ny && ny < m && 0 <= nx && nx < n && grid[ny][nx] == 1)
{
ans += dfs(grid, ny, nx);
}
}
return ans;
}
};
Complexity analysis
-
Time complexity: O(mn), m and n are the number of rows and columns of the two-dimensional array respectively. In the worst case, you need to traverse all the squares once.
-
Spatial complexity: O(mn). Mainly the stack overhead used for recursion.
Reference results
Accepted 728/728 cases passed (16 ms) Your runtime beats 77.67 % of cpp submissions Your memory usage beats 45.27 % of cpp submissions (22.7 MB)
Animation powered by ManimCommunity/manim