1. Red black tree concept
First look at the AVL tree:
AVL tree is a highly balanced binary search tree
Implementation of AVL tree insertion
Look at the red and black trees:
The Red Black tree is also a binary search tree. However, a storage bit is added to each node to represent the color of the node, which can be Red or Black. By limiting the coloring mode of each node on any path from root to leaf, the Red Black tree ensures that no path will be twice longer than other paths, so it is close to balance
Properties of red black tree
- Each node is either red or black
- The root node is black
- If a node is red, its two child nodes are black
- For each node, the simple path from the node to all its descendant leaf nodes contains the same number of black nodes
- Each empty node is black.
After ensuring the above properties, the red black tree ensures that no path will be twice longer than other paths.
Reason: suppose there are 3 black nodes on a path. The shortest path of this tree is all black 3, and the longest path is alternating black and red 6. The longest path is exactly twice as long as the shortest path, just in line with the red black tree structure.
2. Red black tree KV model
Basic structure
#pragma once
#include<iostream>
using namespace std;
enum Color
{
RED = 0, BLACK,
};
template<class Key, class Value>
struct RBTreeNode
{
RBTreeNode<Key, Value>* _left;
RBTreeNode<Key, Value>* _right;
RBTreeNode<Key, Value>* _parent;
pair<Key, Value> _kv;
Color col;
RBTreeNode(const pair<Key, Value>& val)
:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(val), col(RED)//Default node color
{}
};
template<class Key,class Value>
class RBTree
{
typedef RBTreeNode<Key, Value> Node;
public:
RBTree() :_root(nullptr) {}
pair<Node*, bool>Insert(const pair<Key, Value>val);//Insertion of red black tree
private:
Node* _root;
};
3. Insertion of red black tree
The red black tree is based on the binary search tree with its balance constraints. Therefore, the insertion of red black tree can be divided into two steps:
- Insert new nodes according to the tree rules of binary search.
- Modify the node color to maintain the red black tree property
Case 1: the red black tree is empty. At this time, a node is created during insertion, and the color of the node is changed to black.
pair<Node*, bool>Insert(const pair<Key, Value>val)//Insertion of red black tree
{
if (_root == nullptr)
{
_root = new Node(val);
_root->col = BLACK;
return make_pair(_root, true);
}
Case 2:
1. The red black tree is not empty. First traverse the red black tree to find the location to insert. At the same time, find whether there are duplicate nodes. If the insertion of duplicate nodes fails, return the pointer of this position and false. In order to implement the trigeminal chain, a parent pointer is also required to point to the previous node of cur
//Binary search tree insertion
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (cur->_kv.first < val.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > val.first)
{
parent = cur;
cur = cur->_left;
}
else//Duplicate key value, failed to insert
{
return make_pair(cur, false);
}
}
2. After the above function is completed, cur points to nullptr and parent points to the previous location to be connected
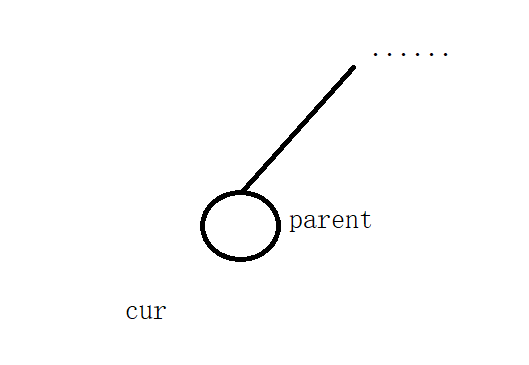
Cur creates a new red node. According to the characteristics of binary search tree, it is also necessary to judge the value of cur node and parent node. If the value of cur node is less than parent, insert it to the left of parent node, otherwise insert it to the right of parent node.
cur = new Node(val);
cur->col = RED;
if (parent->_kv.first > val.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
3. Here, even if the node insertion is completed, we have to adjust the node color of the red black tree to make it comply with the rules of the red black tree. Before that, record the position of the inserted node to return the pair value
The second is to adjust the color of red and black trees
For the convenience of description, record the names of the four nodes cur, parent, uncle and grandparent. The positions of these four nodes are shown in the figure below, referred to as c p u g for short
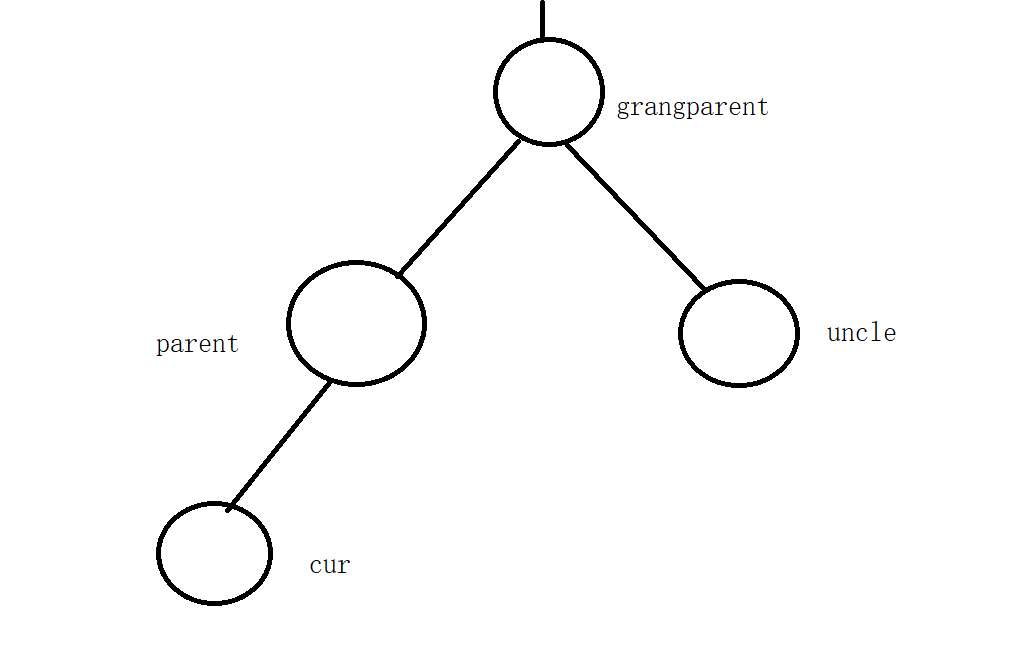
If the inserted parent is black, there is no need to adjust the color of the tree, and the insertion is completed.
The inserted parent is red, and the two red are continuous. Need to deal with
① p is the left subtree of g, cur is red, p is red, g is black, u exists and is red
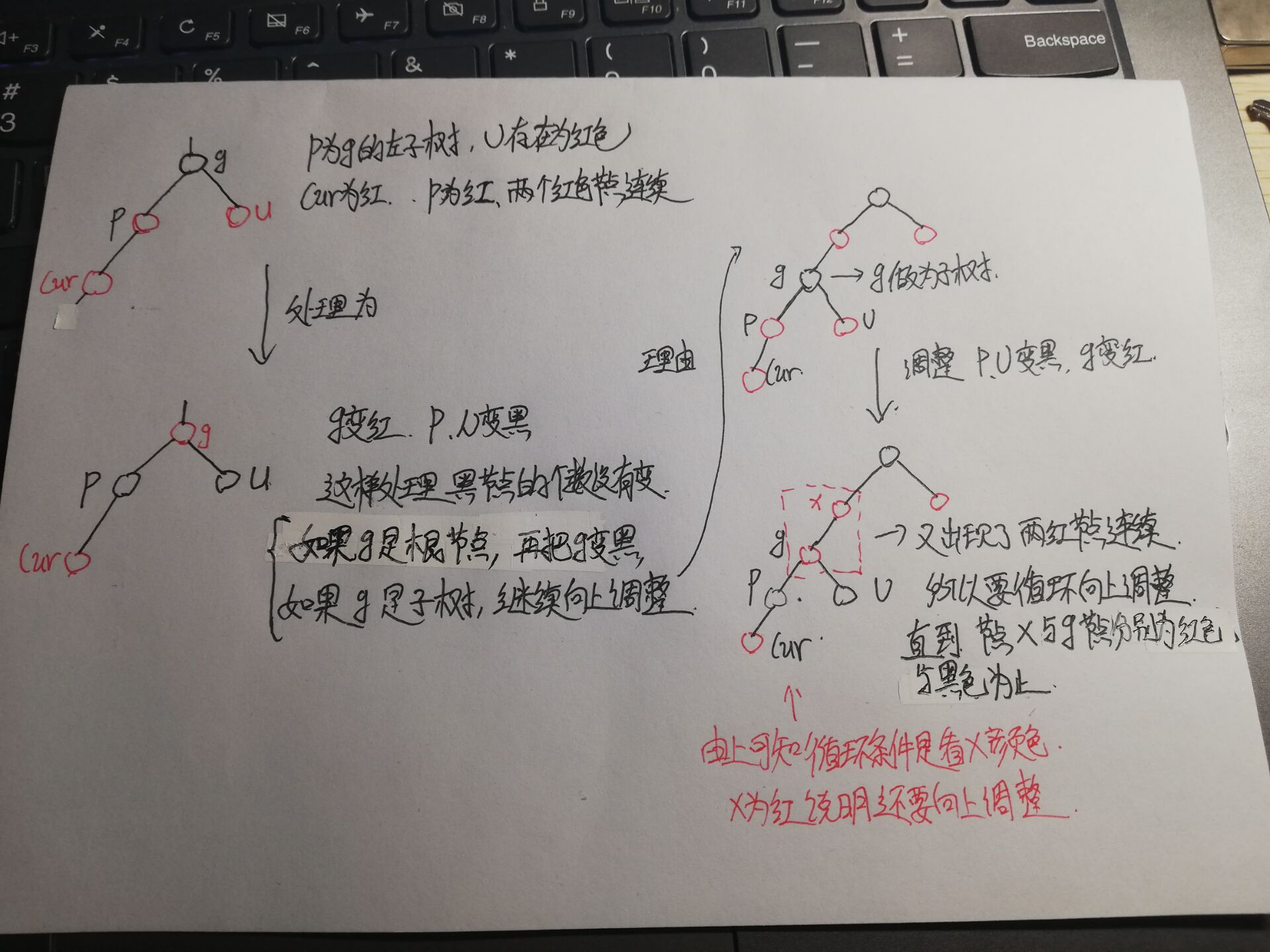
You can write the code according to the figure above
while (parent != nullptr && parent->col == RED)//The stop condition is analyzed in the figure above
{
Node* GradParent = parent->_parent;//Record gradparent node
if (parent == GradParent->_left)//The key is to see the color of the Uncle node
{
Node* Uncle = GradParent->_right;
//Case 1: Uncle exists and is red
if (Uncle && Uncle->col == RED)
{
parent->col = Uncle->col = BLACK;
GradParent->col = RED;
cur = GradParent;//Circular upward judgment
parent = cur->_parent;
}
}
else//parent=GradParent->_right
{
......
}
}
_root->col = BLACK;//Change the color of the root to black to prevent the above process from changing the root node to red
return make_pair(End, true);
② p is the left subtree of g, cur is red, p is red, g is black, u does not exist / u is black (cur,p,g is a straight line)_ Single rotation
First: when this happens, cur must not be a newly inserted node. It must have happened when the color was adjusted upward
reason:
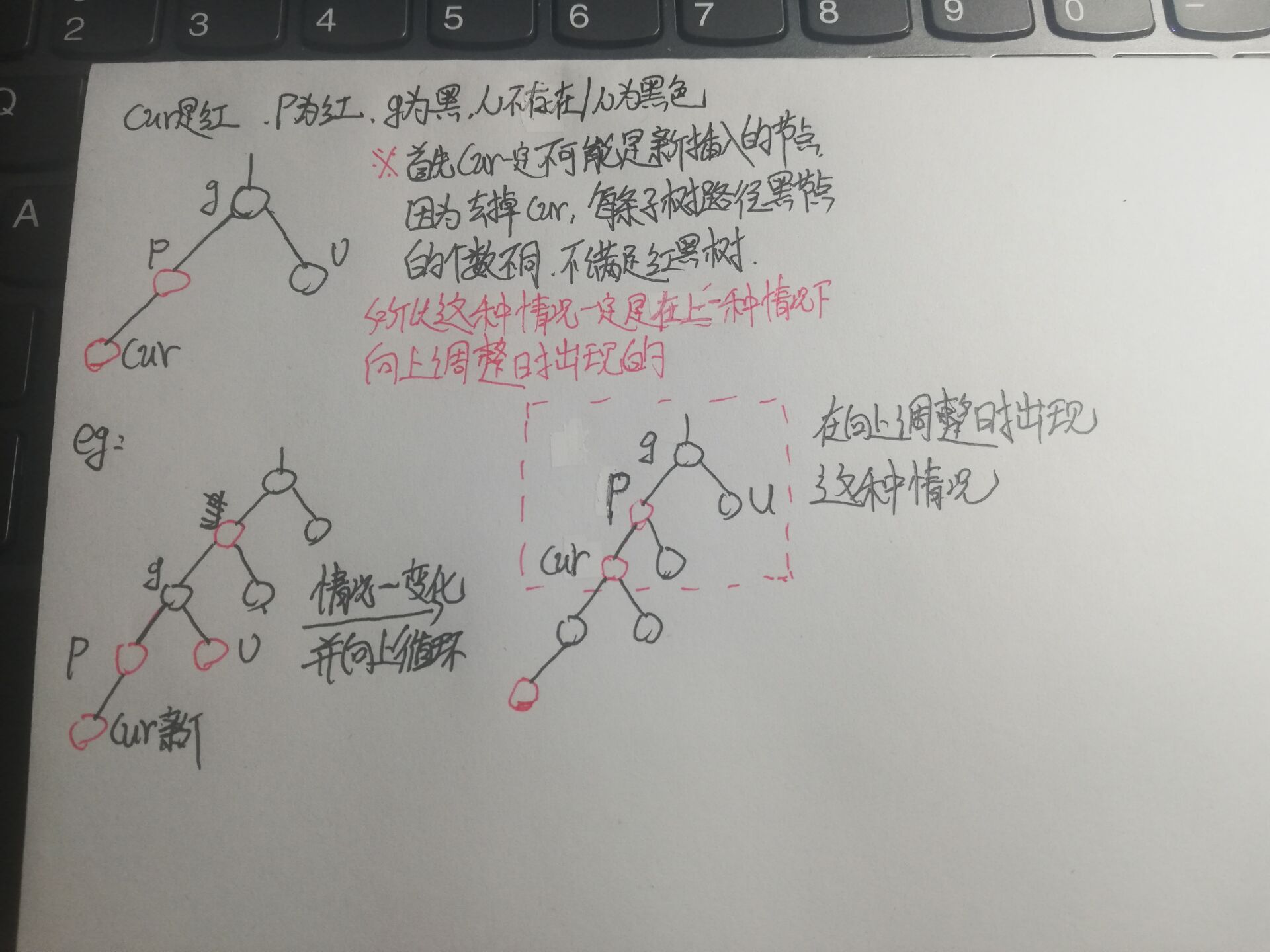
Treatment method:
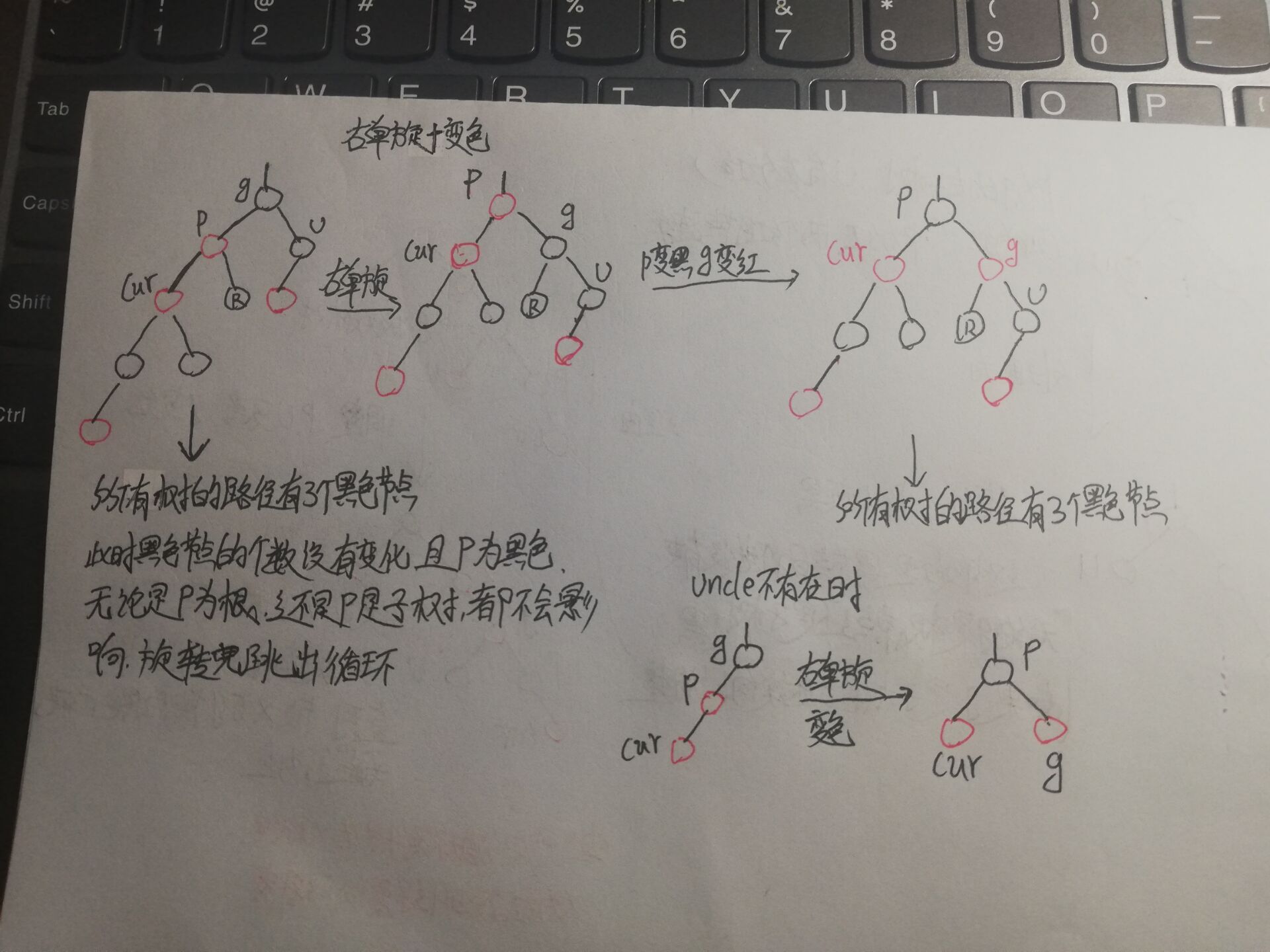
According to the above analysis, we can write the following code
pair<Node*, bool>Insert(const pair<Key, Value>val)//Insertion of red black tree
{
if (_root == nullptr)
{
_root = new Node(val);
_root->col = BLACK;
return make_pair(_root, true);
}
//Binary search tree insertion
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (cur->_kv.first < val.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > val.first)
{
parent = cur;
cur = cur->_left;
}
else//Duplicate key value, failed to insert
{
return make_pair(cur, false);
}
}
cur = new Node(val);
cur->col = RED;
if (parent->_kv.first > val.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
Node* End = cur;//Node that records the insertion location
//Control path
while (parent != nullptr && parent->col == RED)
{
Node* GradParent = parent->_parent;
if (parent == GradParent->_left)//The key is to see the color of the Uncle node
{
Node* Uncle = GradParent->_right;
//Case 1: Uncle exists and is red
if (Uncle && Uncle->col == RED)
{
parent->col = Uncle->col = BLACK;
GradParent->col = RED;
cur = GradParent;
parent = cur->_parent;
}
else//Uncle does not exist or is black
{
if (cur == parent->_left)//Right high, right rotation
{
_Single_Right(GradParent);
GradParent->col = RED;
parent->col = BLACK;
}
break;//After rotation, the number of black nodes remains unchanged and directly jump out of the cycle
}
else//parent=GradParent->_right
{
......
}
}
_root->col = BLACK;//Change the color of the root to black to prevent it from jumping out of the root and turning red
return make_pair(End, true);
}
The right single rotation code is similar to the right rotation of AVL tree. Write the code according to the rotation diagram below
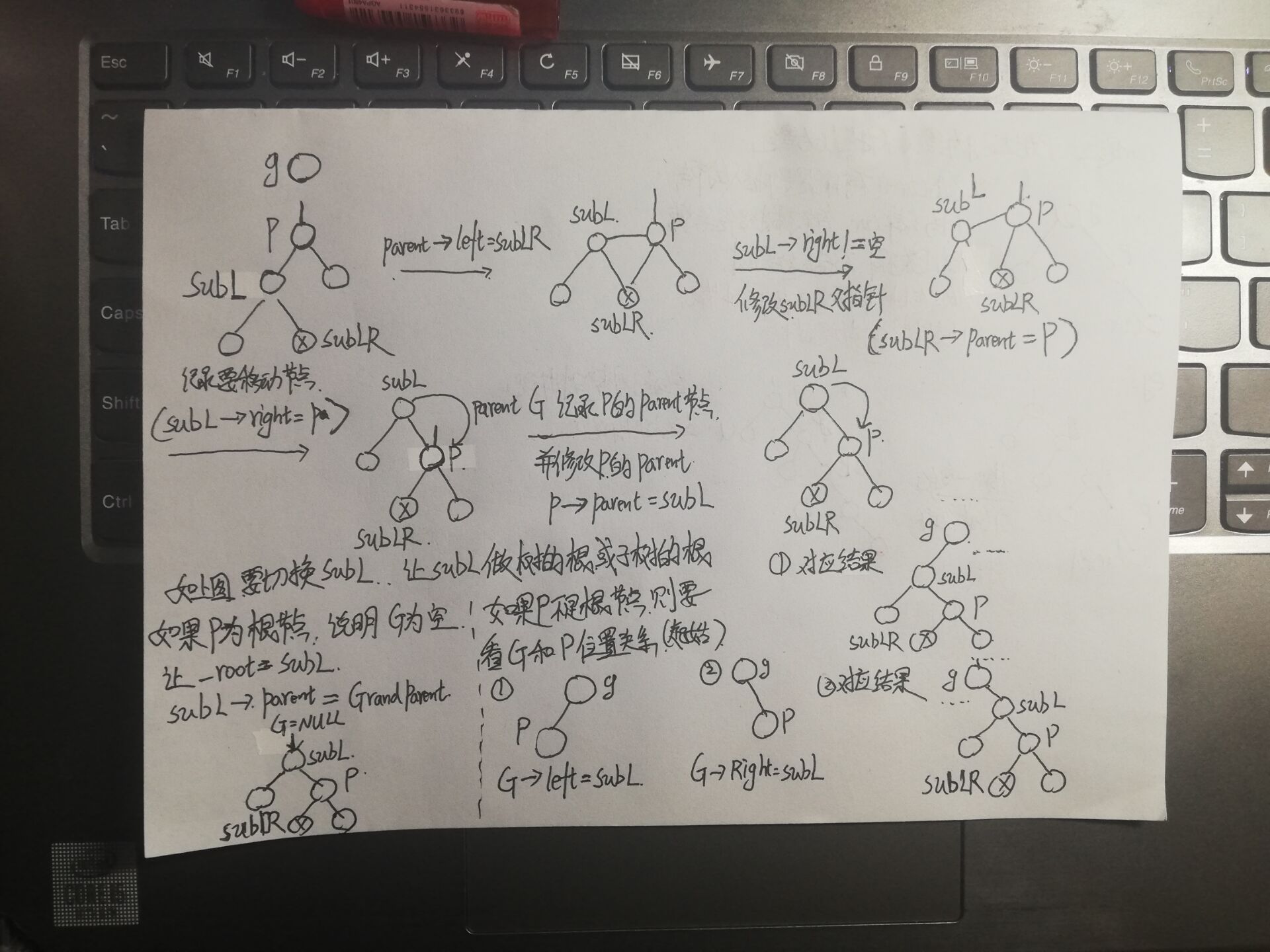
void _Single_Right(Node* parent)//The right single rotation connects the correspondence according to the figure
{
//Record the node to be moved
Node* SubL = parent->_left;
Node* SubLR = SubL->_right;
//connect
parent->_left = SubLR;
if (SubL->_right != nullptr)//Modify parent pointer
{
SubLR->_parent = parent;
}
//connect
SubL->_right = parent;
Node* GradParent = parent->_parent;//Record the parent node of this node in order to modify the root node
parent->_parent = SubL;//Modify parent pointer
//Adjust root node
if (parent == _root)//The node to rotate is the root node
{
_root = SubL;
SubL->_parent = GradParent;
}
else//If the node to be rotated is a subtree, modify the GradParent pointer
{
if (GradParent->_left == parent)
{
GradParent->_left = SubL;
}
else
{
GradParent->_right = SubL;
}
SubL->_parent = GradParent;
}
}
③ p is the left subtree of g, cur is red, p is red, g is black, u does not exist / u is black (cur,p,g are broken lines)_ Double rotation
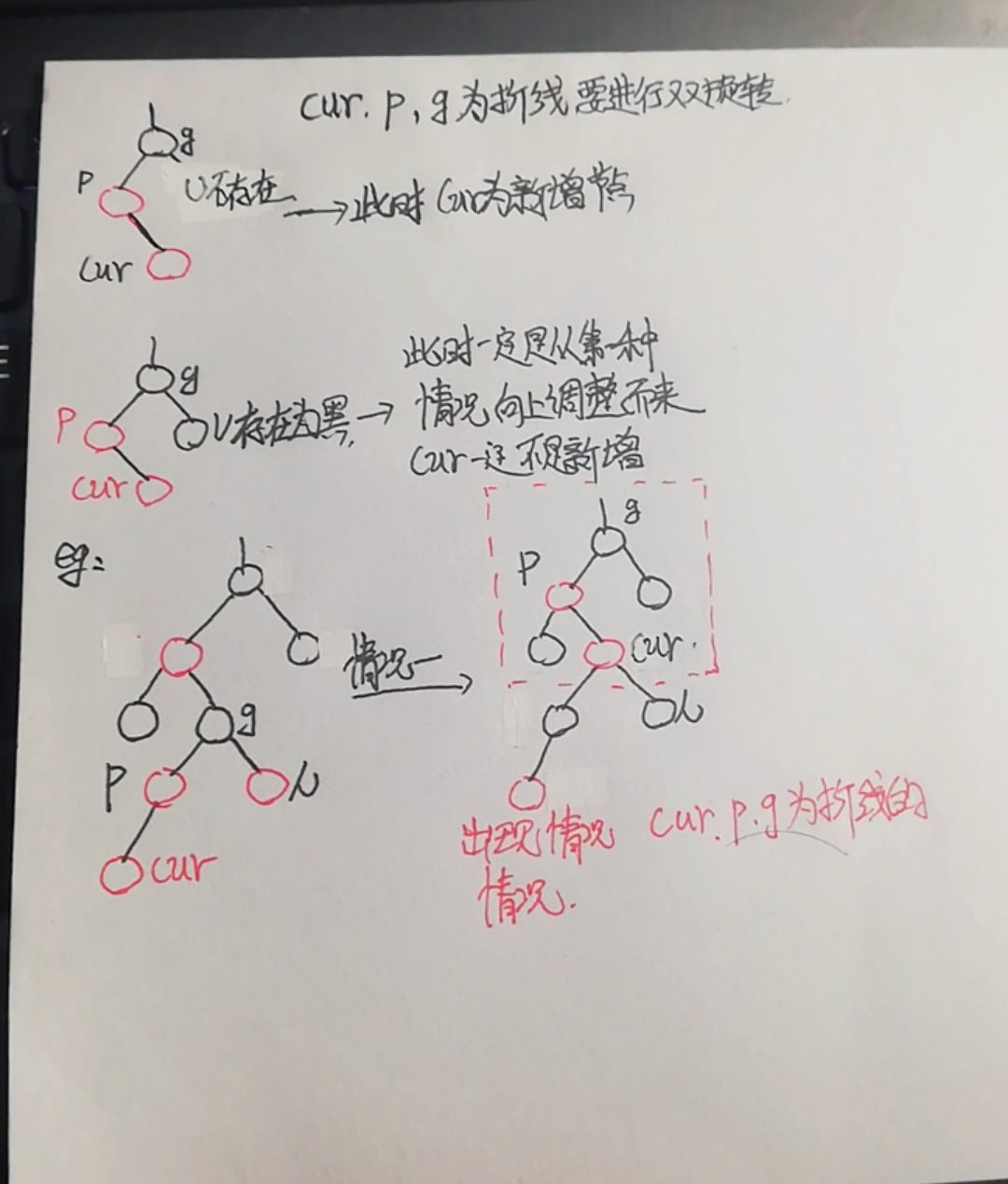
Treatment method:
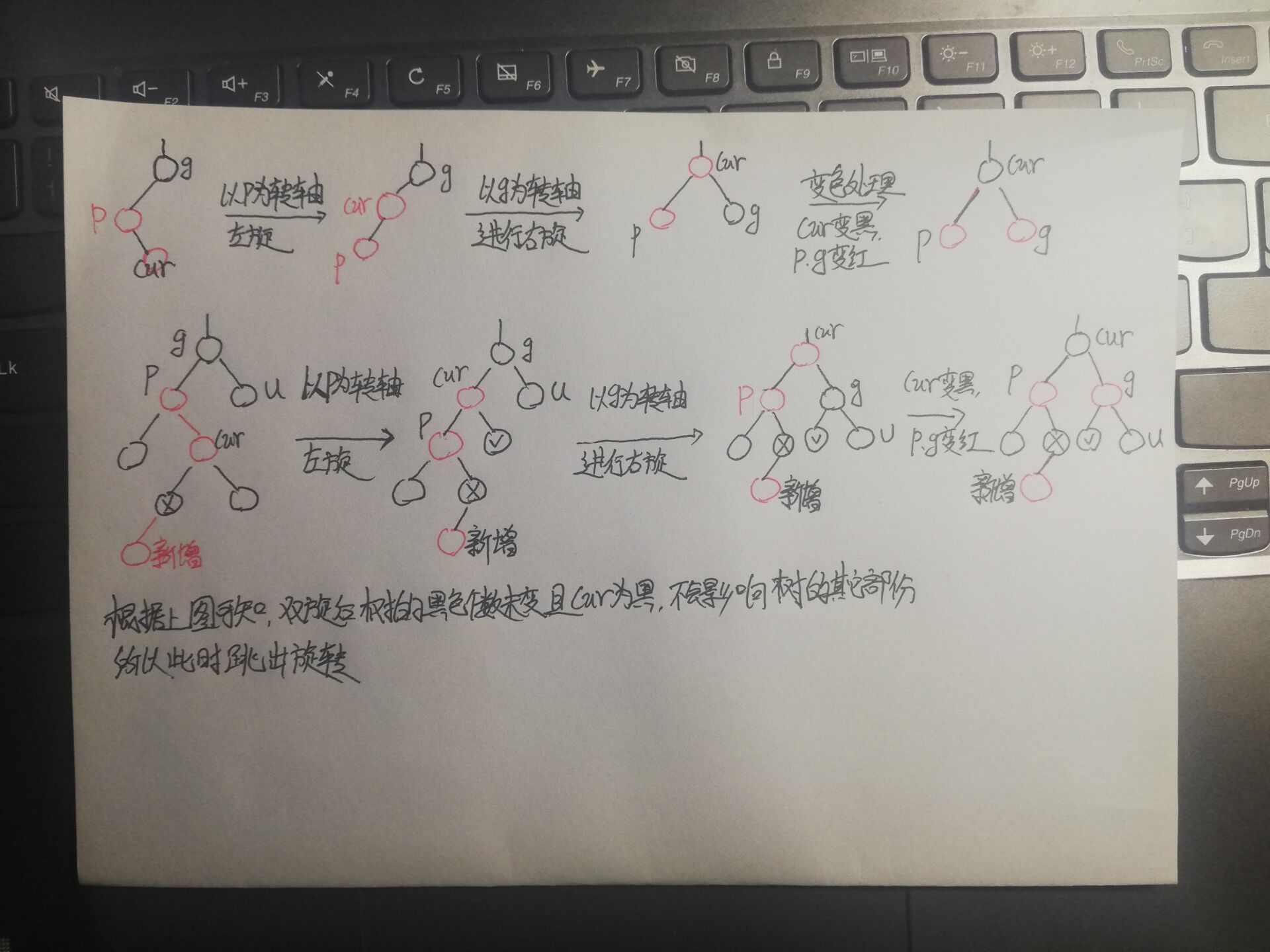
Write the code according to the figure above
pair<Node*, bool>Insert(const pair<Key, Value>val)//Insertion of red black tree
{
if (_root == nullptr)
{
_root = new Node(val);
_root->col = BLACK;
return make_pair(_root, true);
}
//Binary search tree insertion
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (cur->_kv.first < val.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > val.first)
{
parent = cur;
cur = cur->_left;
}
else//Duplicate key value, failed to insert
{
return make_pair(cur, false);
}
}
cur = new Node(val);
cur->col = RED;
if (parent->_kv.first > val.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
Node* End = cur;//Node that records the insertion location
//Control path
while (parent != nullptr && parent->col == RED)
{
Node* GradParent = parent->_parent;
if (parent == GradParent->_left)//The key is to see the color of the Uncle node
{
Node* Uncle = GradParent->_right;
//Case 1: Uncle exists and is red
if (Uncle && Uncle->col == RED)
{
parent->col = Uncle->col = BLACK;
GradParent->col = RED;
cur = GradParent;
parent = cur->_parent;
}
else//Uncle does not exist or is black
{
if (cur == parent->_left)//Right high, right rotation
{
_Single_Right(GradParent);
GradParent->col = RED;
parent->col = BLACK;
}
else//Broken line shape, left and right double rotation
{
_Single_Left(parent);
_Single_Right(GradParent);
cur->col = BLACK;
parent->col = GradParent->col = RED;
}
break;//After rotation, the number of black nodes remains unchanged and directly jump out of the cycle
}
else//parent=GradParent->_right
{
......
}
}
_root->col = BLACK;//Change the color of the root to black to prevent the above process from changing the root node to red
return make_pair(End, true);
}
The left single rotation is similar to the left single rotation of AVL tree, and the rotation principle is the same as that of the right single rotation picture, so it is not repeated
void _Single_Left(Node* parent)//Left rotation
{
//Record the node to be moved
Node* SubR = parent->_right;
Node* SubRL = SubR->_left;
//connect
parent->_right = SubRL;
if (SubRL != nullptr)
{
SubRL->_parent = parent;
}
SubR->_left = parent;
Node* GradParent = parent->_parent;//Record the parent node of this node in order to modify the root node
parent->_parent = SubR;
//Adjust root node
if (parent == _root)
{
_root = SubR;
SubR->_parent = GradParent;
}
else //If the node to be rotated is a subtree, modify the GradParent pointer
{
if (GradParent->_left == parent)//The rotation is the left subtree, connected to the left
{
GradParent->_left = SubR;
}
else
{
GradParent->_right = SubR;//conversely
}
SubR->_parent = GradParent;
}
}
④ p is the right subtree of g, cur is red, p is red, g is black, u exists and is red
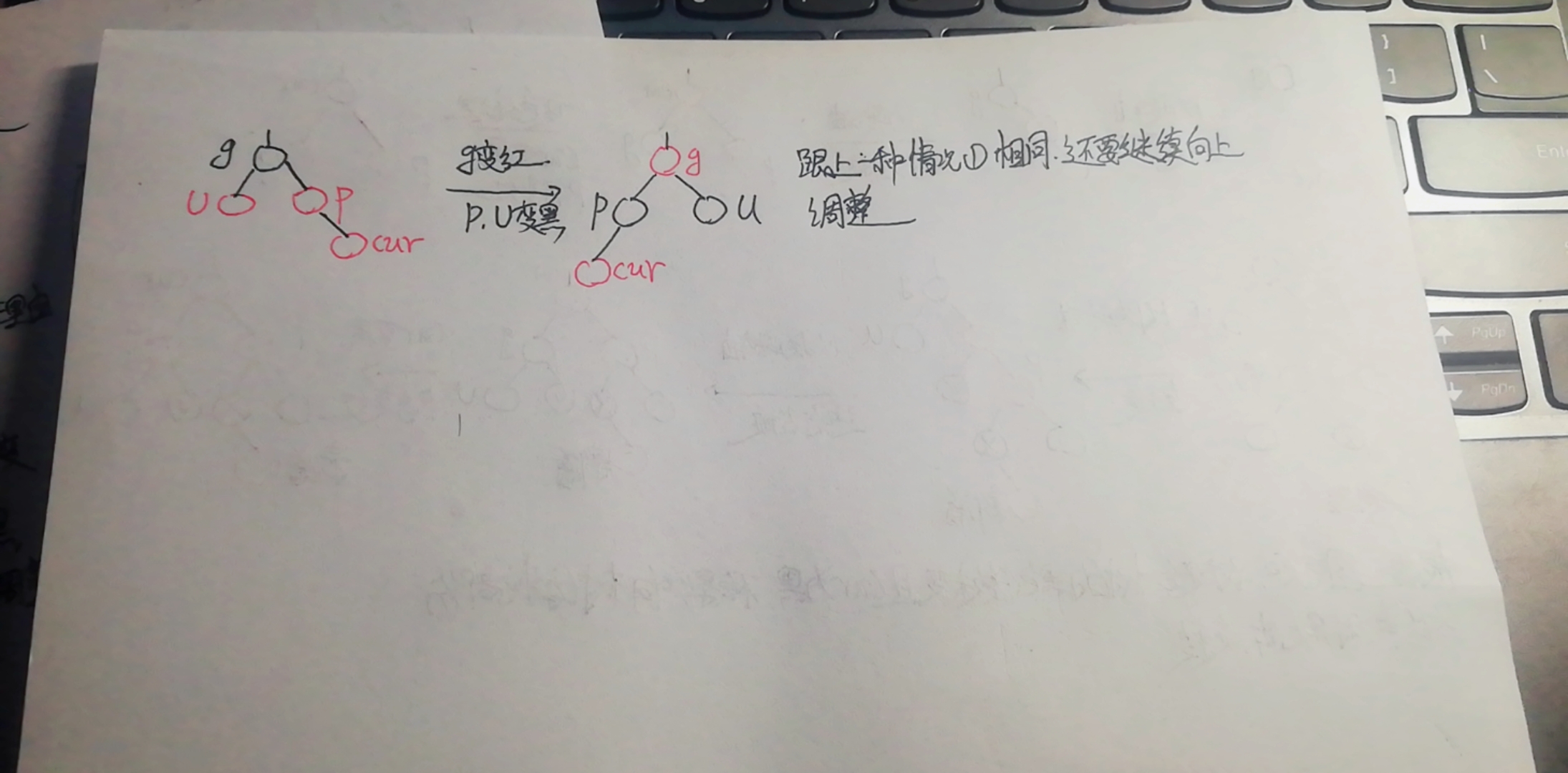
This situation is the same as ①, so it is not repeated
⑤ p is the right subtree of g, cur is red, p is red, g is black, u does not exist / u is black (cur,p,g is a straight line)_ Single rotation
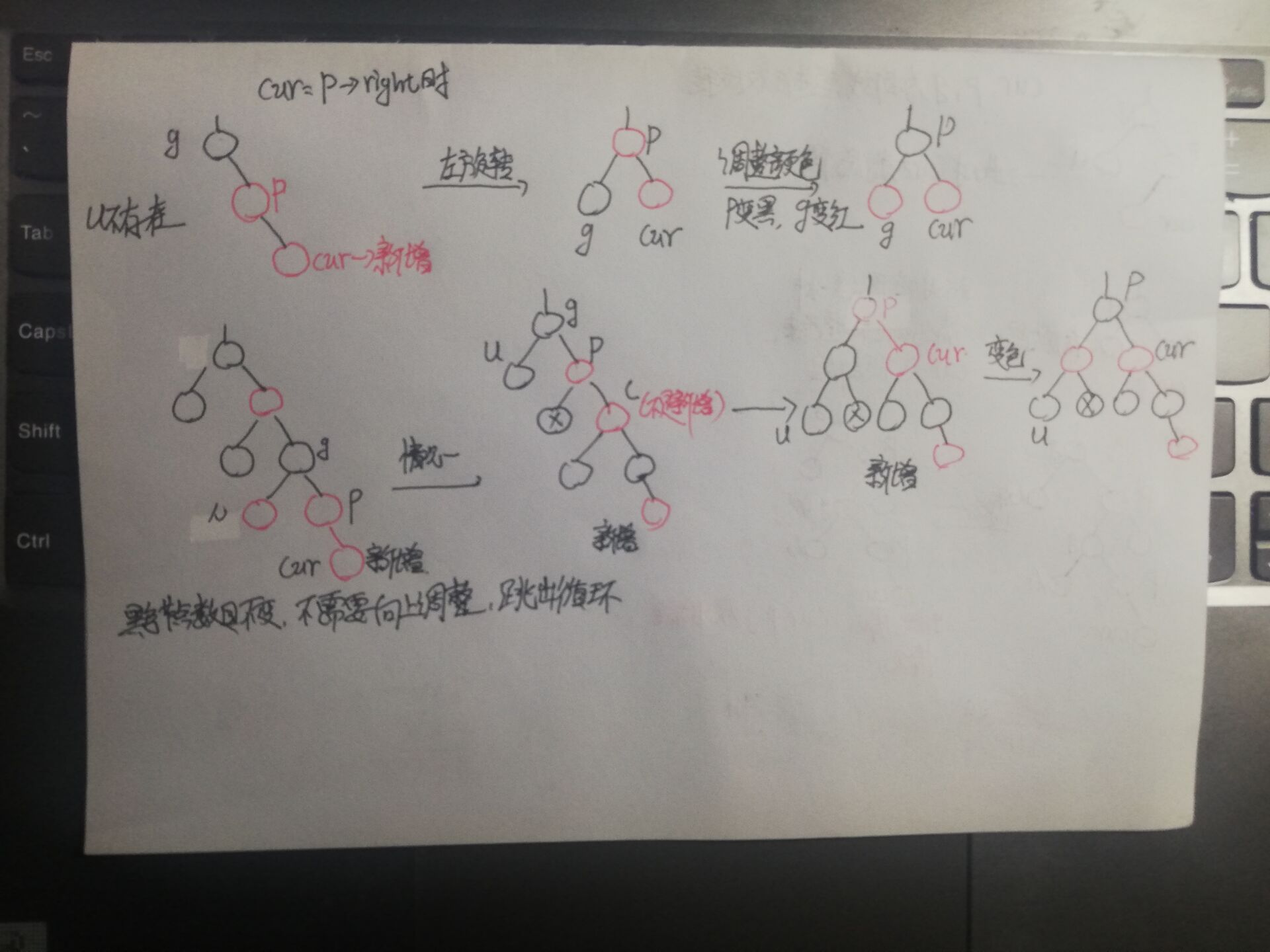
⑥ p is the right subtree of g, cur is red, p is red, g is black, u does not exist / u is black (cur,p,g are broken lines)_ Double rotation
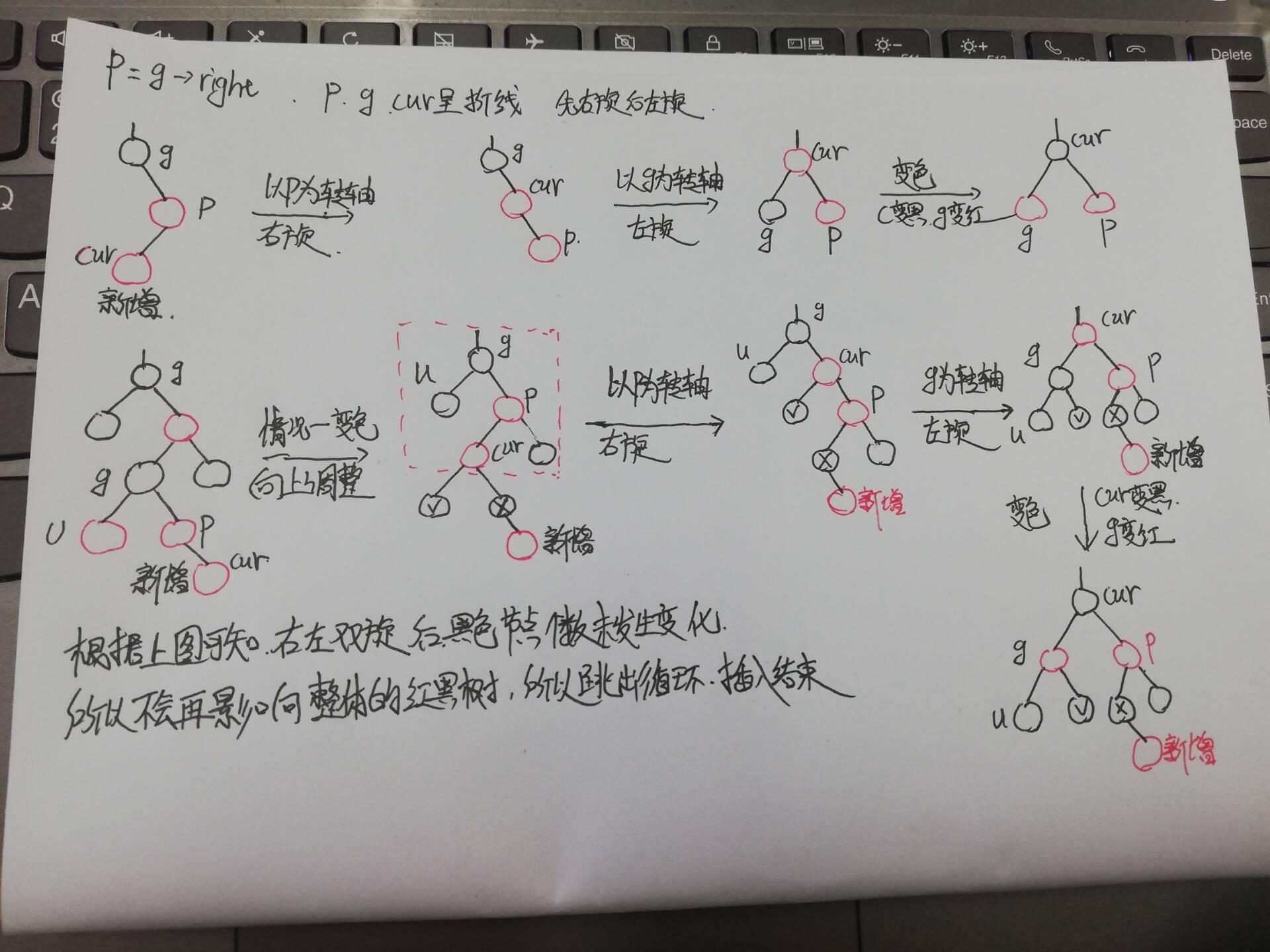
According to the above figure, the lower half logic of red black tree insertion can be written
Insertion code of red black tree
pair<Node*, bool>Insert(const pair<Key, Value>val)//Insertion of red black tree
{
if (_root == nullptr)
{
_root = new Node(val);
_root->col = BLACK;
return make_pair(_root, true);
}
//Binary search tree insertion
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (cur->_kv.first < val.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > val.first)
{
parent = cur;
cur = cur->_left;
}
else//Duplicate key value, failed to insert
{
return make_pair(cur, false);
}
}
cur = new Node(val);
cur->col = RED;
if (parent->_kv.first > val.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
Node* End = cur;//Node that records the insertion location
//Control path
while (parent != nullptr && parent->col == RED)
{
Node* GradParent = parent->_parent;
if (parent == GradParent->_left)//The key is to see the color of the Uncle node
{
Node* Uncle = GradParent->_right;
//Case 1: Uncle exists and is red
if (Uncle && Uncle->col == RED)
{
parent->col = Uncle->col = BLACK;
GradParent->col = RED;
cur = GradParent;
parent = cur->_parent;
}
else//Uncle does not exist or is black
{
if (cur == parent->_left)//Right high, right rotation
{
_Single_Right(GradParent);
GradParent->col = RED;
parent->col = BLACK;
}
else//Broken line shape, left and right double rotation
{
_Single_Left(parent);
_Single_Right(GradParent);
cur->col = BLACK;
parent->col = GradParent->col = RED;
}
break;//After rotation, the number of black nodes remains unchanged and directly jump out of the cycle
}
}
else//parent=GradParent->_right
{
Node* Uncle = GradParent->_left;
if (Uncle != nullptr && Uncle->col == RED)
{
Uncle->col = parent->col = BLACK;
GradParent->col = RED;
cur = GradParent;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)//Left high, left rotation
{
_Single_Left(GradParent);
GradParent->col = RED;
parent->col = BLACK;
}
else//Polyline, right left double rotation
{
_Single_Right(parent);
_Single_Left(GradParent);
cur->col = BLACK;
GradParent->col = RED;
}
break;
}
}
}
_root->col = BLACK;//Change the color of the root to black to prevent the root node from jumping out of the loop in the first case, and the root node turns red
return make_pair(End, true);
}
//Private: rotation code
void _Single_Right(Node* parent)//The right single rotation connects the correspondence according to the figure
{
//Record the node to be moved
Node* SubL = parent->_left;
Node* SubLR = SubL->_right;
//connect
parent->_left = SubLR;
if (SubL->_right != nullptr)//Modify parent pointer
{
SubLR->_parent = parent;
}
//connect
SubL->_right = parent;
Node* GradParent = parent->_parent;//Record the parent node of this node in order to modify the root node
parent->_parent = SubL;//Modify parent pointer
//Adjust root node
if (parent == _root)//The node to rotate is the root node
{
_root = SubL;
SubL->_parent = GradParent;
}
else//If the node to be rotated is a subtree, modify the GradParent pointer
{
if (GradParent->_left == parent)
{
GradParent->_left = SubL;
}
else
{
GradParent->_right = SubL;
}
SubL->_parent = GradParent;
}
}
void _Single_Left(Node* parent)//Left rotation
{
//Record the node to be moved
Node* SubR = parent->_right;
Node* SubRL = SubR->_left;
//connect
parent->_right = SubRL;
if (SubRL != nullptr)
{
SubRL->_parent = parent;
}
SubR->_left = parent;
Node* GradParent = parent->_parent;//Record the parent node of this node in order to modify the root node
parent->_parent = SubR;
//Adjust root node
if (parent == _root)
{
_root = SubR;
SubR->_parent = GradParent;
}
else //If the node to be rotated is a subtree, modify the GradParent pointer
{
if (GradParent->_left == parent)//The rotation is the left subtree, connected to the left
{
GradParent->_left = SubR;
}
else
{
GradParent->_right = SubR;//conversely
}
SubR->_parent = GradParent;
}
}
4. Judge whether a tree is a red black tree
bool CheckRBTree()
{
if (_root == nullptr)
{
return true;
}
else if(_root->col == RED)
{
cout << "The root node is red" << endl;
return false;
}
//First record the number of black nodes on the leftmost node, and take this number as the benchmark to check other paths
int NumBack = 0;
Node* LeftBack = _root;
while (LeftBack != nullptr)
{
if (LeftBack->col == BLACK)
{
NumBack++;
}
LeftBack = LeftBack->_left;
}
int Num = 0;//Check the variable of the number of black nodes in other channels
return _CheckRBTree(_root, NumBack, Num);
}
//Private:
bool _CheckRBTree(Node* root, const int NumBack, int Num)
{
if (root == nullptr)//If it is empty, it means to traverse to the bottom of the red black tree and jump out of the loop condition
{
//Check the number of black nodes and NumBack on this road
if (NumBack != Num)
{
cout << "The number of black nodes is different" << endl;
return false;
}
else
{
return true;
}
}
//Preorder traversal
if (root->col == RED && root->_parent->col == RED)
{
cout << "Red node continuous" << endl;
return false;
}
else if (root->col == BLACK)
{
Num++;
}
return _CheckRBTree(root->_left, NumBack, Num) && _CheckRBTree(root->_right, NumBack, Num);
}
5. The red black tree finds nodes by the key value key
You can traverse the red black tree once, which is a simple binary search tree. I won't repeat it
Node* Find(const Key& key)//Returns the node pointer through key value lookup
{
Node* cur = _root;
Node* ret = nullptr;
while (cur != nullptr)
{
if (key > cur->_kv.first)
{
cur = cur->_right;
}
else if (key < cur->_kv.first)
{
cur = cur->_left;
}
else
{
ret = cur;
break;
}
}
return ret;
}
6. Printing of red and black trees
Medium order printing red black tree
void PrintInord()
{
return _PrintInord(_root);
}
//Private:
void _PrintInord(Node* root)//Medium order printing
{
if (root == nullptr)
return;
_PrintInord(root->_left);
cout << root->_kv.first << "->" << root->_kv.second << endl;
_PrintInord(root->_right);
}
7. Destructor of red black tree
Postorder ergodic destructor
~RBTree()
{
_Destory(_root);//Postorder traversal
_root = nullptr;
}
//Private:
void _Destory(Node* root)//Postorder traversal
{
if (root == nullptr)
{
return;
}
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
8. Insert, search and judge the complete code of red black tree
#pragma once
#include<iostream>
using namespace std;
enum Color
{
RED = 0, BLACK,
};
template<class Key, class Value>
struct RBTreeNode
{
RBTreeNode<Key, Value>* _left;
RBTreeNode<Key, Value>* _right;
RBTreeNode<Key, Value>* _parent;
pair<Key, Value> _kv;
Color col;
RBTreeNode(const pair<Key, Value>& val)
:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(val), col(RED)//Default node color
{}
};
template<class Key, class Value>
class RBTree
{
typedef RBTreeNode<Key, Value> Node;
public:
RBTree() :_root(nullptr) {}
~RBTree()
{
_Destory(_root);//Postorder traversal
_root = nullptr;
}
bool CheckRBTree()
{
if (_root == nullptr)
{
return true;
}
else if(_root->col == RED)
{
cout << "The root node is red" << endl;
return false;
}
//Record the number of black nodes on the leftmost node first
int NumBack = 0;
Node* LeftBack = _root;
while (LeftBack != nullptr)
{
if (LeftBack->col == BLACK)
{
NumBack++;
}
LeftBack = LeftBack->_left;
}
int Num = 0;//Record the number of black nodes at this time
return _CheckRBTree(_root, NumBack, Num);
}
Node* Find(const Key& key)//Returns the node pointer through key value lookup
{
Node* cur = _root;
Node* ret = nullptr;
while (cur != nullptr)
{
if (key > cur->_kv.first)
{
cur = cur->_right;
}
else if (key < cur->_kv.first)
{
cur = cur->_left;
}
else
{
ret = cur;
break;
}
}
return ret;
}
//Print red black tree
void PrintInord()
{
return _PrintInord(_root);
}
pair<Node*, bool>Insert(const pair<Key, Value>val)//Insertion of red black tree
{
if (_root == nullptr)
{
_root = new Node(val);
_root->col = BLACK;
return make_pair(_root, true);
}
//Binary search tree insertion
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (cur->_kv.first < val.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > val.first)
{
parent = cur;
cur = cur->_left;
}
else//Duplicate key value, failed to insert
{
return make_pair(cur, false);
}
}
cur = new Node(val);
cur->col = RED;
if (parent->_kv.first > val.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
Node* End = cur;//Node that records the insertion location
//Control path
while (parent != nullptr && parent->col == RED)
{
Node* GradParent = parent->_parent;
if (parent == GradParent->_left)//The key is to see the color of the Uncle node
{
Node* Uncle = GradParent->_right;
//Case 1: Uncle exists and is red
if (Uncle && Uncle->col == RED)
{
parent->col = Uncle->col = BLACK;
GradParent->col = RED;
cur = GradParent;
parent = cur->_parent;
}
else//Uncle does not exist or is black
{
if (cur == parent->_left)//Right high, right rotation
{
_Single_Right(GradParent);
GradParent->col = RED;
parent->col = BLACK;
}
else//Broken line shape, left and right double rotation
{
_Single_Left(parent);
_Single_Right(GradParent);
cur->col = BLACK;
parent->col = GradParent->col = RED;
}
break;//After rotation, the number of black nodes remains unchanged and directly jump out of the cycle
}
}
else//parent=GradParent->_right
{
Node* Uncle = GradParent->_left;
if (Uncle != nullptr && Uncle->col == RED)
{
Uncle->col = parent->col = BLACK;
GradParent->col = RED;
cur = GradParent;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)//Left high, left rotation
{
_Single_Left(GradParent);
GradParent->col = RED;
parent->col = BLACK;
}
else//Polyline, right left double rotation
{
_Single_Right(parent);
_Single_Left(GradParent);
cur->col = BLACK;
GradParent->col = RED;
}
break;
}
}
}
_root->col = BLACK;//Change the color of the root to black to prevent the above process from changing the root node to red
return make_pair(End, true);
}
private:
Node* _root;
void _PrintInord(Node* root)
{
if (root == nullptr)
return;
_PrintInord(root->_left);
cout << root->_kv.first << "->" << root->_kv.second << endl;
_PrintInord(root->_right);
}
bool _CheckRBTree(Node* root, const int NumBack, int Num)
{
if (root == nullptr)
{
//Check the number of black nodes and NumBack on this road
if (NumBack != Num)
{
cout << "The number of black nodes is different" << endl;
return false;
}
else
{
return true;
}
}
//Preorder traversal
if (root->col == RED && root->_parent->col == RED)
{
cout << "Red node continuous" << endl;
return false;
}
else if (root->col == BLACK)
{
Num++;
}
return _CheckRBTree(root->_left, NumBack, Num) && _CheckRBTree(root->_right, NumBack, Num);
}
void _Destory(Node* root)//Postorder traversal
{
if (root == nullptr)
{
return;
}
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
void _Single_Right(Node* parent)//The right single rotation connects the correspondence according to the figure
{
//Record the node to be moved
Node* SubL = parent->_left;
Node* SubLR = SubL->_right;
//connect
parent->_left = SubLR;
if (SubL->_right != nullptr)//Modify parent pointer
{
SubLR->_parent = parent;
}
//connect
SubL->_right = parent;
Node* GradParent = parent->_parent;//Record the parent node of this node in order to modify the root node
parent->_parent = SubL;//Modify parent pointer
//Adjust root node
if (parent == _root)//The node to rotate is the root node
{
_root = SubL;
SubL->_parent = GradParent;
}
else//If the node to be rotated is a subtree, modify the GradParent pointer
{
if (GradParent->_left == parent)
{
GradParent->_left = SubL;
}
else
{
GradParent->_right = SubL;
}
SubL->_parent = GradParent;
}
}
void _Single_Left(Node* parent)//Left rotation
{
//Record the node to be moved
Node* SubR = parent->_right;
Node* SubRL = SubR->_left;
//connect
parent->_right = SubRL;
if (SubRL != nullptr)
{
SubRL->_parent = parent;
}
SubR->_left = parent;
Node* GradParent = parent->_parent;//Record the parent node of this node in order to modify the root node
parent->_parent = SubR;
//Adjust root node
if (parent == _root)
{
_root = SubR;
SubR->_parent = GradParent;
}
else //If the node to be rotated is a subtree, modify the GradParent pointer
{
if (GradParent->_left == parent)//The rotation is the left subtree, connected to the left
{
GradParent->_left = SubR;
}
else
{
GradParent->_right = SubR;//conversely
}
SubR->_parent = GradParent;
}
}
};
9. Test red and black trees
#include"RBTree.h" / / header file of red black tree
#include<stdlib.h>
#include<time.h>
void Test()//Test inserting and printing the red black tree to judge the red black tree
{
int arr[] = { 3,2,5,1,7,11,6,15 };
RBTree<int, int>t;
for (const auto& e : arr)
{
t.Insert(make_pair(e, e));
}
t.PrintInord();
if (t.CheckRBTree())
{
cout << "Is RedBlackTree" << endl;
}
else
{
cout << "Is Not RedBlackTree" << endl;
}
}
//Random insertion of red black tree
void Test2()
{
int n = 20;
RBTree<int, int>t;
srand((unsigned int)time(0));
for (int i = 0; i < n; i++)
{
int tmp = rand();
t.Insert(make_pair(tmp,tmp));
}
t.PrintInord();
if (t.CheckRBTree())
{
cout << "Is RedBlackTree" << endl;
}
else
{
cout << "Is Not RedBlackTree" << endl;
}
}
int main()
{
Test();
Test2();
return 0;
}
The operation result is: